9709_m23_qp

Question 1

Topic 1.3 – Coordinate geometry

A line has equation $y = 3x – 2k$ and a curve has equation $y = x^2 – kx + 2$, where $k$ is a constant.

Show that the line and the curve meet for all values of $k$.

▶️Answer/Explanation

Set the equations equal:

\[ 3x – 2k = x^2 – kx + 2 \]

Rearrange:
\[ x^2 – kx + 2 – 3x + 2k = 0 \]
\[ x^2 – (k + 3)x + (2k + 2) = 0 \]

For intersection, this quadratic in $x$ must have at least one real root. Check the discriminant:
\[ \Delta = (k + 3)^2 – 4 \cdot 1 \cdot (2k + 2) \]
\[ = k^2 + 6k + 9 – (8k + 8) \]
\[ = k^2 + 6k + 9 – 8k – 8 \]
\[ = k^2 – 2k + 1 \]
\[ = (k – 1)^2 \]

Since $(k – 1)^2 \geq 0$ for all real $k$ (and equals 0 when $k = 1$), $\Delta \geq 0$. Thus, there are always real roots (two if $k \neq 1$, one if $k = 1$), meaning the line and curve meet for all $k$.

Final Answer:

The discriminant $(k – 1)^2 \geq 0$ for all $k$, so the line and curve always intersect.

Question 2

Topic 1.2 – Functions

A function f is defined by $f(x) = x^2 – 2x + 5$ for $x \in \mathbb{R}$. A sequence of transformations is applied in the following order to the graph of $y = f(x)$ to give the graph of $y = g(x)$:

* Stretch parallel to the x-axis with scale factor $\frac{1}{2}$
* Reflection in the y-axis
* Stretch parallel to the y-axis with scale factor 3

Find $g(x)$, giving your answer in the form $ax^2 + bx + c$, where $a$, $b$, and $c$ are constants.

▶️Answer/Explanation

Start with $f(x) = x^2 – 2x + 5$

1. Stretch parallel to the x-axis, scale factor $\frac{1}{2}$:
Replace $x$ with $2x$ (since $x’ = 2x$):
\[ f(2x) = (2x)^2 – 2(2x) + 5 = 4x^2 – 4x + 5 \]

2. Reflection in the y-axis:
Replace $x$ with $-x$:
\[ f(2(-x)) = 4(-x)^2 – 4(-x) + 5 = 4x^2 + 4x + 5 \]

3. Stretch parallel to the y-axis, scale factor 3:
Multiply the function by 3:
\[ g(x) = 3(4x^2 + 4x + 5) = 12x^2 + 12x + 15 \]

Final Answer:

$g(x) = 12x^2 + 12x + 15$

Question 3

Topic 1.7 – Differentiation

A curve has equation $y = \frac{1}{60}(3x + 1)^2$ and a point is moving along the curve.

Find the x-coordinate of the point on the curve at which the x- and y-coordinates are increasing at the same rate.

▶️Answer/Explanation

Curve: $y = \frac{1}{60}(3x + 1)^2$.

“Same rate” means $\frac{dy}{dt} = \frac{dx}{dt}$. Using the chain rule: $\frac{dy}{dt} = \frac{dy}{dx} \cdot \frac{dx}{dt}$.

Find $\frac{dy}{dx}$:
\[ y = \frac{1}{60}(3x + 1)^2 \]
\[ \frac{dy}{dx} = \frac{1}{60} \cdot 2 (3x + 1) \cdot 3 = \frac{1}{10}(3x + 1) \]

Set $\frac{dy}{dt} = \frac{dx}{dt}$:
\[ \frac{dy}{dx} \cdot \frac{dx}{dt} = \frac{dx}{dt} \]
\[ \frac{1}{10}(3x + 1) \cdot \frac{dx}{dt} = \frac{dx}{dt} \]
\[ \frac{1}{10}(3x + 1) = 1 \quad (\text{assuming } \frac{dx}{dt} \neq 0\text{)} \]
\[ 3x + 1 = 10 \]
\[ 3x = 9 \]
\[ x = 3 \]

Final Answer:

$x = 3$

Question 4

Topic 1.6 – Series

The circumference round the trunk of a large tree is measured and found to be 5.00 m. After one year, the circumference is measured again and found to be 5.02 m.

(a) Given that the circumferences at yearly intervals form an arithmetic progression, find the circumference 20 years after the first measurement.

(b) Given instead that the circumferences at yearly intervals form a geometric progression, find the circumference 20 years after the first measurement.

▶️Answer/Explanation

(a) Arithmetic Progression (AP)

In an arithmetic progression, the difference between consecutive terms is constant. Here, the circumference increases from 5.00 m to 5.02 m in one year, so the common difference is:

Common difference ($d$) = 5.02 m – 5.00 m = 0.02 m
First term ($a$) = 5.00 m

The formula for the $n$-th term of an AP is:
\[
a_n = a + (n – 1) \cdot d
\]

We want the circumference 20 years after the first measurement, which is the 21st term (since the first measurement is year 1, the second is year 2, and 20 years later is year 21). So, $n = 21$:
\[
a_{21} = 5.00 + (21 – 1) \cdot 0.02 = 5.00 + 20 \cdot 0.02 = 5.00 + 0.40 = 5.40 \, \text{m}
\]

Answer (a): The circumference after 20 years is 5.40 m.

(b) Geometric Progression (GP)

In a geometric progression, each term is multiplied by a constant ratio. The circumference goes from 5.00 m to 5.02 m in one year, so the common ratio is:

Common ratio ($r$) = 5.02 / 5.00 = 1.004
First term ($a$) = 5.00 m

The formula for the $n$-th term of a GP is:
\[
a_n = a \cdot r^{n-1}
\]

Again, we want the circumference 20 years after the first measurement, which is the 21st term ($n = 21$):
\[
a_{21} = 5.00 \cdot (1.004)^{20}
\]

Now, calculate $1.004^{20}$:
Using a calculator, $1.004^{20} \approx 1.08328$ (rounded for simplicity).
So, $a_{21} = 5.00 \cdot 1.08328 \approx 5.4164 \, \text{m}$.

Answer (b): The circumference after 20 years is approximately 5.42 m (rounded to 2 decimal places).

Final Answers:

(a) 5.40 m (Arithmetic Progression)
(b) 5.42 m (Geometric Progression)

Question 5

Topic 1.3 – Coordinate geometry

Points A(7, 12) and B lie on a circle with center (-2, 5). The line AB has equation y = -2x + 26.

Find the coordinates of B.

▶️Answer/Explanation

Given: A(7, 12), center (-2, 5), line $ y = -2x + 26 $. Find B.

Radius = distance from center (-2, 5) to A(7, 12):
$ \sqrt{(7 + 2)^2 + (12 – 5)^2} = \sqrt{9^2 + 7^2} = \sqrt{130} $.
B($ x, y $) on line: $ y = -2x + 26 $.
Distance from center to B = radius:
$ \sqrt{(x + 2)^2 + (-2x + 21)^2} = \sqrt{130} $ (since $ y – 5 = -2x + 21 $).
Square it: $ (x + 2)^2 + (-2x + 21)^2 = 130 $.
Expand: $ x^2 + 4x + 4 + 4x^2 – 84x + 441 = 5x^2 – 80x + 445 $.
Set equal: $ 5x^2 – 80x + 445 = 130 $.
Simplify: $ 5x^2 – 80x + 315 = 0 $.
Divide by 5: $ x^2 – 16x + 63 = 0 $.
Factor: $ (x – 7)(x – 9) = 0 $.
$ x = 7 $: $ y = -2(7) + 26 = 12 $ (this is A).
$ x = 9 $: $ y = -2(9) + 26 = 8 $ (this is B).

Final Answer:
B is (9, 8).

Question 6

Topic 1.6 – Series

In the expansion of $\left(\frac{x}{a} + \frac{a}{x^2}\right)^7$, it is given that

$\frac{\text{the coefficient of } x^4}{\text{the coefficient of } x} = 3$.

Find the possible values of the constant $a$.

▶️Answer/Explanation

The expansion is a sum of 8 terms (from $ k = 0 $ to 7). Each term is:

$ \binom{7}{k} \left( \frac{x}{a} \right)^{7-k} \left( \frac{a}{x^2} \right)^k = \binom{7}{k} \frac{x^{7-3k}}{a^{7-2k}} $.

Find Terms
For $ x^4 $: $ 7 – 3k = 4 $
$ 3k = 3 $, $ k = 1 $.
Term: $ \binom{7}{1} \frac{x^4}{a^{7-2}} = 7 \frac{x^4}{a^5} $.
Coefficient: $ \frac{7}{a^5} $.
For $ x $ (i.e., $ x^1 $): $ 7 – 3k = 1 $
$ 3k = 6 $, $ k = 2 $.
Term: $ \binom{7}{2} \frac{x^1}{a^{7-4}} = 21 \frac{x}{a^3} $.
Coefficient: $ \frac{21}{a^3} $.

Ratio
$ \frac{\text{Coeff of } x^4}{\text{Coeff of } x} = \frac{\frac{7}{a^5}}{\frac{21}{a^3}} = \frac{7}{21} \cdot \frac{a^3}{a^5} = \frac{1}{3} \cdot \frac{1}{a^2} = \frac{1}{3a^2} $.
Given: $ \frac{1}{3a^2} = 3 $.

Solve
$ 1 = 9a^2 $,
$ a^2 = \frac{1}{9} $,
$ a = \frac{1}{3} $ or $ -\frac{1}{3} $.

Final Answer:

$ a = \frac{1}{3} $ or $ -\frac{1}{3} $.

Question 7

Topic 1.5 – Trigonometry

(a) By first obtaining a quadratic equation in $\cos \theta$, solve the equation

$\tan \theta \sin \theta = 1$

for $0^{\circ} < \theta < 360^{\circ}$.

(b) Show that $\frac{\tan \theta}{\sin \theta} – \frac{\sin \theta}{\tan \theta} = \tan \theta \sin \theta$.

▶️Answer/Explanation

(a) Solve $ \tan \theta \sin \theta = 1 $ for $ 0^\circ < \theta < 360^\circ $

Step 1: Rewrite $ \tan \theta = \frac{\sin \theta}{\cos \theta} $, so the equation becomes:
\[
\frac{\sin \theta}{\cos \theta} \cdot \sin \theta = 1 \quad \text{or} \quad \frac{\sin^2 \theta}{\cos \theta} = 1.
\]
Step 2: Multiply both sides by $ \cos \theta $ (assuming $ \cos \theta \neq 0 $):
\[
\sin^2 \theta = \cos \theta.
\]
Step 3: Use $ \sin^2 \theta = 1 – \cos^2 \theta $ to form a quadratic:
\[
1 – \cos^2 \theta = \cos \theta.
\]
Step 4: Rearrange:
\[
1 – \cos^2 \theta – \cos \theta = 0 \quad \text{or} \quad \cos^2 \theta + \cos \theta – 1 = 0.
\]
Step 5: Let $ x = \cos \theta $. Solve the quadratic $ x^2 + x – 1 = 0 $:
Discriminant: $ 1^2 – 4 \cdot 1 \cdot (-1) = 1 + 4 = 5 $.
$ x = \frac{-1 \pm \sqrt{5}}{2} $.
$ x = \frac{-1 + \sqrt{5}}{2} \approx 0.618 $ or $ x = \frac{-1 – \sqrt{5}}{2} \approx -1.618 $.
Step 6: Since $ \cos \theta $ is between -1 and 1, discard $ -1.618 $. Use $ \cos \theta = \frac{-1 + \sqrt{5}}{2} $.
Step 7: Find $ \theta $ in $ 0^\circ < \theta < 360^\circ $:
$ \cos \theta \approx 0.618 $, so $ \theta = \cos^{-1}(0.618) \approx 51.8^\circ $ (1st quadrant).
Also, $ \theta = 360^\circ – 51.8^\circ = 308.2^\circ $ (4th quadrant, since $ \cos \theta $ is positive there too).

Answer: $ \theta = 51.8^\circ $ or $ 308.2^\circ $ (approximate).

(b) Show $ \frac{\tan \theta}{\sin \theta} – \frac{\sin \theta}{\tan \theta} = \tan \theta \sin \theta $

Step 1: Substitute $ \tan \theta = \frac{\sin \theta}{\cos \theta} $:
Left side: $ \frac{\tan \theta}{\sin \theta} – \frac{\sin \theta}{\tan \theta} = \frac{\frac{\sin \theta}{\cos \theta}}{\sin \theta} – \frac{\sin \theta}{\frac{\sin \theta}{\cos \theta}} $.
Step 2: Simplify each term:
$ \frac{\frac{\sin \theta}{\cos \theta}}{\sin \theta} = \frac{\sin \theta}{\cos \theta} \cdot \frac{1}{\sin \theta} = \frac{1}{\cos \theta} $,
$ \frac{\sin \theta}{\frac{\sin \theta}{\cos \theta}} = \sin \theta \cdot \frac{\cos \theta}{\sin \theta} = \cos \theta $.
Step 3: Combine:
$ \frac{1}{\cos \theta} – \cos \theta $.
Step 4: Rewrite with a common denominator ($ \cos \theta $):
$ \frac{1}{\cos \theta} – \cos \theta = \frac{1 – \cos^2 \theta}{\cos \theta} $.
Step 5: Use $ 1 – \cos^2 \theta = \sin^2 \theta $:
$ \frac{\sin^2 \theta}{\cos \theta} = \sin \theta \cdot \frac{\sin \theta}{\cos \theta} = \sin \theta \cdot \tan \theta $.
Result: Matches the right side, $ \tan \theta \sin \theta $.

Answer: It’s shown (they’re equal).

Final Answers:

(a) $ \theta = 51.8^\circ $ or $ 308.2^\circ $
(b) Proven: $ \frac{\tan \theta}{\sin \theta} – \frac{\sin \theta}{\tan \theta} = \tan \theta \sin \theta $

Question 8

Topic 1.4 – Circular measure

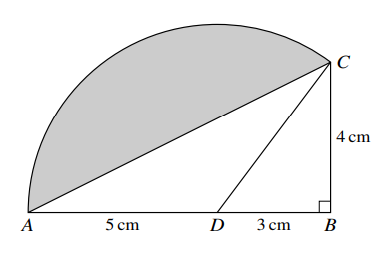
The diagram shows triangle ABC in which angle B is a right angle. The length of AB is 8 cm and the length of BC is 4 cm. The point D on AB is such that $AD=5~cm$. The sector DAC is part of a circle with centre D.

(a) Find the perimeter of the shaded region.

(b) Find the area of the shaded region.

▶️Answer/Explanation

Solution: –

8(a)

$tan~BDC=\frac{4}{3}$ or $sin~BDC=\frac{4}{5}$ or $cos~BDC=\frac{3}{5}$ used to find ADC

$BDC=0.927[3]~\rightarrow~ADC=\pi-0.927[3]~[=2.214to2.215]$

$Arc~AC=5\times their~2.214$

$AC=\sqrt{8^{2}+4^{2}}$ or $2\times5\times sin~1.107$

$[Perimeter=11.07+8.94]=20.0$

8(b)

$Sector~ACD=\frac{1}{2}\times5^{2}\times their~2.214$

$Subtracting~the~area~of~\Delta ADC=\frac{1}{2}\times5\times4$ or $\frac{1}{2}5^{2}~sin~their~2.214$ or $\frac{1}{2}\times8\times4-\frac{1}{2}\times3\times4$

$Shaded~area=27.7-10=17.7$

Question 9

Topic 1.2 – Functions

The function f is defined by $f(x) = -3x^2 + 2$ for $x \leq -1$.

(a) State the range of f.

(b) Find an expression for $f^{-1}(x)$.

The function g is defined by $g(x) = -x^2 – 1$ for $x \leq -1$.

▶️Answer/Explanation

(a) State the range of $ f(x) = -3x^2 + 2 $ for $ x \leq -1 $

Since $ x \leq -1 $, $ x^2 \geq 1 $ (e.g., at $ x = -1 $, $ x^2 = 1 $; at $ x = -2 $, $ x^2 = 4 $).
$ -3x^2 \leq -3 $ (multiply by -3, which is negative).
Add 2: $ -3x^2 + 2 \leq -3 + 2 = -1 $.
Max value at $ x = -1 $: $ f(-1) = -3(1) + 2 = -1 $.
As $ x $ gets more negative (e.g., $ x = -2 $), $ f(-2) = -3(4) + 2 = -10 $, so it decreases without bound.
Range: all values $ \leq -1 $.

Answer: $ f(x) \leq -1 $.

(b) Find $ f^{-1}(x) $ for $ f(x) = -3x^2 + 2 $
Set $ y = -3x^2 + 2 $.
Solve for $ x $:
$ y – 2 = -3x^2 $,
$ x^2 = \frac{2 – y}{3} $,
$ x = \pm \sqrt{\frac{2 – y}{3}} $.
Since $ x \leq -1 $ (domain of $ f $), take the negative root: $ x = -\sqrt{\frac{2 – y}{3}} $.
So, $ f^{-1}(x) = -\sqrt{\frac{2 – x}{3}} $.
Domain of $ f^{-1} $ is the range of $ f $: $ x \leq -1 $.

Answer: $ f^{-1}(x) = -\sqrt{\frac{2 – x}{3}} $.

(c) Solve $ fg(x) – gf(x) + 8 = 0 $ where $ g(x) = -x^2 – 1 $ for $ x \leq -1 $
$ fg(x) = f(g(x)) = f(-x^2 – 1) $:
$ g(x) = -x^2 – 1 $,
$ f(-x^2 – 1) = -3(-x^2 – 1)^2 + 2 $.
Expand: $ (-x^2 – 1)^2 = x^4 + 2x^2 + 1 $,
$ -3(x^4 + 2x^2 + 1) + 2 = -3x^4 – 6x^2 – 3 + 2 = -3x^4 – 6x^2 – 1 $.
$ gf(x) = g(f(x)) = g(-3x^2 + 2) $:
$ f(x) = -3x^2 + 2 $,
$ g(-3x^2 + 2) = -(-3x^2 + 2)^2 – 1 $.
Expand: $ (-3x^2 + 2)^2 = 9x^4 – 12x^2 + 4 $,
$ -(9x^4 – 12x^2 + 4) – 1 = -9x^4 + 12x^2 – 4 – 1 = -9x^4 + 12x^2 – 5 $.
Equation: $ fg(x) – gf(x) + 8 = 0 $:
$ (-3x^4 – 6x^2 – 1) – (-9x^4 + 12x^2 – 5) + 8 = 0 $.
Simplify: $ -3x^4 – 6x^2 – 1 + 9x^4 – 12x^2 + 5 + 8 = 6x^4 – 18x^2 + 12 = 0 $.
Divide by 6: $ x^4 – 3x^2 + 2 = 0 $.
Let $ u = x^2 $ (since $ x \leq -1 $, $ u \geq 1 $):
$ u^2 – 3u + 2 = 0 $.
Factor: $ (u – 1)(u – 2) = 0 $.
$ u = 1 $ or $ u = 2 $.
$ u = x^2 $:
$ x^2 = 1 $, $ x = -1 $ (since $ x \leq -1 $).
$ x^2 = 2 $, $ x = -\sqrt{2} $ (since $ -\sqrt{2} \approx -1.414 < -1 $).

Answer: $ x = -1 $ or $ x = -\sqrt{2} $.

Final Answers:

(a) $ f(x) \leq -1 $
(b) $ f^{-1}(x) = -\sqrt{\frac{2 – x}{3}} $
(c) $ x = -1 $ or $ -\sqrt{2} $

Question 10

(a) Topic 1.7 – Differentiation

(b) Topic 1.8 – Integration

(c) Topic 1.7 – Differentiation

(d) Topic 1.7 – Differentiation

At the point (4, -1) on a curve, the gradient of the curve is $-\frac{3}{2}$. It is given that $\frac{dy}{dx} = x^{-\frac{1}{2}} + k$, where $k$ is a constant.

(a) Show that $k = -2$.

(b) Find the equation of the curve.

(d) Determine the nature of the stationary point.

▶️Answer/Explanation

(a) Show that $ k = -2 $

Given: At $ (4, -1) $, the gradient $ \frac{dy}{dx} = -\frac{3}{2} $.
Also, $ \frac{dy}{dx} = x^{-\frac{1}{2}} + k $.
At $ x = 4 $:
$ x^{-\frac{1}{2}} = 4^{-\frac{1}{2}} = \frac{1}{\sqrt{4}} = \frac{1}{2} $.
So, $ \frac{dy}{dx} = \frac{1}{2} + k $.
Set equal to the given gradient: $ \frac{1}{2} + k = -\frac{3}{2} $.
Solve: $ k = -\frac{3}{2} – \frac{1}{2} = -\frac{4}{2} = -2 $.

Answer: $ k = -2 $ (shown).

(b) Find the equation of the curve

$ \frac{dy}{dx} = x^{-\frac{1}{2}} + k = x^{-\frac{1}{2}} – 2 $ (using $ k = -2 $).
Integrate:
$ \int x^{-\frac{1}{2}} \, dx = \int x^{-\frac{1}{2}} \, dx = 2x^{\frac{1}{2}} $,
$ \int -2 \, dx = -2x $,
$ y = 2x^{\frac{1}{2}} – 2x + c $.
Use point $ (4, -1) $:
$ y = -1 $, $ x = 4 $,
$ -1 = 2\sqrt{4} – 2(4) + c = 2(2) – 8 + c = 4 – 8 + c = -4 + c $,
$ c = -1 + 4 = 3 $.
Equation: $ y = 2x^{\frac{1}{2}} – 2x + 3 $.

Answer: $ y = 2\sqrt{x} – 2x + 3 $.

Stationary point: $ \frac{dy}{dx} = 0 $.
$ \frac{dy}{dx} = x^{-\frac{1}{2}} – 2 = 0 $,
$ x^{-\frac{1}{2}} = 2 $,
$ \frac{1}{\sqrt{x}} = 2 $,
$ \sqrt{x} = \frac{1}{2} $,
$ x = \frac{1}{4} $.
Find $ y $ at $ x = \frac{1}{4} $:
$ y = 2\sqrt{\frac{1}{4}} – 2\left(\frac{1}{4}\right) + 3 = 2\left(\frac{1}{2}\right) – \frac{1}{2} + 3 = 1 – 0.5 + 3 = 3.5 $.

Answer: $ \left( \frac{1}{4}, 3.5 \right) $.

(d) Determine the nature of the stationary point

Use the second derivative: $ \frac{dy}{dx} = x^{-\frac{1}{2}} – 2 $.
$ \frac{d^2y}{dx^2} = \frac{d}{dx} (x^{-\frac{1}{2}}) = -\frac{1}{2} x^{-\frac{3}{2}} $.
At $ x = \frac{1}{4} $:
$ x^{-\frac{3}{2}} = \left(\frac{1}{4}\right)^{-\frac{3}{2}} = 4^{\frac{3}{2}} = (\sqrt{4})^3 = 2^3 = 8 $,
$ \frac{d^2y}{dx^2} = -\frac{1}{2} \cdot 8 = -4 $.
Since $ \frac{d^2y}{dx^2} < 0 $, it’s a maximum.

Answer: Maximum.

Final Answers:

(a) $ k = -2 $ (shown)
(b) $ y = 2\sqrt{x} – 2x + 3 $
(c) $ \left( \frac{1}{4}, 3.5 \right) $
(d) Maximum

Question 11

(a) Topic 1.3 – Coordinate geometry

(b) Topic 1.8 – Integration

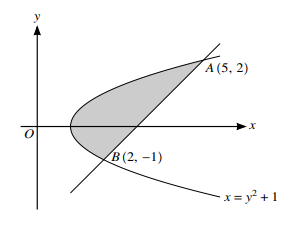
The diagram shows the curve with equation $x = y^2 + 1$. The points A(5, 2) and B(2, -1) lie on the curve.

(a) Find an equation of the line AB.

(b) Find the volume of revolution when the region between the curve and the line AB is rotated through 360° about the y-axis.

▶️Answer/Explanation

Solution: –

11(a)

Gradient of AB = $\frac{2-(-1)}{5-2}$

Equation of AB is $y-2=1(x-5)$ or $y+1=l(x-2)$

11(b)

$[\pi]\int x^{2}dy=[\pi]\int[(y+1)^{2}+1]dy=[\pi]\int[(y^{2}+2y+1)+1]dy$

$[\pi]\int\left[\frac{y^{3}}{3}+\frac{2y^{2}}{2}+y\right]$

$[\pi]\int(y+3)^{2}dy=[\pi]\int(y^{2}+6y+9)dy$

$[\pi]\left[\frac{y^{3}}{3}+3y^{2}+9y\right]$ or $[\pi]\left[\frac{(y+3)^{3}}{3}\right]$

$[\pi]\left\{\frac{8}{3}+12+18-\left(-\frac{1}{3}+3-9\right)\right\}$ or $[\pi]\left\{\frac{32}{5}+\frac{16}{3}+2-\left(-\frac{1}{5}-\frac{2}{3}-1\right)\right\}$

Volume = $\pi \left[ \left( 39 – 15 \frac{3}{5} \right) \right]$

= $23 \frac{2}{5} \pi$ or $\frac{117}{5} \pi$ or awrt $73.5$ [1327]

Resources

Members

Company