CIE AS/A Level Chemistry 2.3 Formulae Study Notes- 2025-2027 Syllabus
CIE AS/A Level Chemistry 2.3 Formulae Study Notes – New Syllabus
CIE AS/A Level Chemistry 2.3 Formulae Study Notes at IITian Academy focus on specific topic and type of questions asked in actual exam. Study Notes focus on AS/A Level Chemistry latest syllabus with Candidates should be able to:
- write formulas of ionic compounds from ionic charges and oxidation numbers (shown by a Roman numeral), including:
(a) the prediction of ionic charge from the position of an element in the Periodic Table
(b) recall of the names and formulas for the following ions: NO3– , CO3 2–, SO4 2–, OH– , NH4+ , Zn2+, Ag+,HCO3–, PO43– - (a) write and construct equations (which should be balanced), including ionic equations (which should not include spectator ions)
(b) use appropriate state symbols in equations - define and use the terms empirical and molecular formula
- understand and use the terms anhydrous, hydrated and water of crystallisation
- calculate empirical and molecular formulas, using given data
Writing Formulae of Ionic Compounds — Using Ionic Charges & Oxidation Numbers
Ionic compounds consist of positive ions (cations) and negative ions (anions). Their formulas are written by balancing the charges so that the overall compound is electrically neutral.
Total positive charge \( = \) total negative charge
1. Predicting Ionic Charge from the Periodic Table
The group number determines the likely ionic charge:
| Group | Type of ion | Typical charge | Examples |
|---|---|---|---|
| 1 | Cation | \( +1 \) | \( \mathrm{Li^+,\ Na^+,\ K^+} \) |
| 2 | Cation | \( +2 \) | \( \mathrm{Mg^{2+},\ Ca^{2+}} \) |
| 3 | Cation | \( +3 \) | \( \mathrm{Al^{3+}} \) |
| 5 | Anion | \( -3 \) | \( \mathrm{N^{3-},\ P^{3-}} \) |
| 6 | Anion | \( -2 \) | \( \mathrm{O^{2-},\ S^{2-}} \) |
| 7 | Anion | \( -1 \) | \( \mathrm{F^{-},\ Cl^{-},\ Br^{-}} \) |
Transition metals often form more than one ion — their oxidation state is shown by a Roman numeral.
Examples: \( \mathrm{Fe^{2+}} \) (iron(II)), \( \mathrm{Fe^{3+}} \) (iron(III)), \( \mathrm{Cu^+} \) (copper(I)), \( \mathrm{Cu^{2+}} \) (copper(II))
2. Common Ions to Recall
These ions must be known and memorised:
| Ion name | Formula |
|---|---|
| Nitrate | \( \mathrm{NO_3^-} \) |
| Carbonate | \( \mathrm{CO_3^{2-}} \) |
| Sulfate | \( \mathrm{SO_4^{2-}} \) |
| Hydroxide | \( \mathrm{OH^-} \) |
| Ammonium | \( \mathrm{NH_4^+} \) |
| Zinc ion | \( \mathrm{Zn^{2+}} \) |
| Silver ion | \( \mathrm{Ag^+} \) |
| Hydrogencarbonate | \( \mathrm{HCO_3^-} \) |
| Phosphate | \( \mathrm{PO_4^{3-}} \) |
3. Writing Formulas of Ionic Compounds
The charges must cancel out. Swap and drop the charges (making them subscripts) and simplify if needed.
Example: \( \mathrm{Mg^{2+}} \) and \( \mathrm{Cl^-} \) → \( \mathrm{MgCl_2} \)
![]()
If an ion is a compound ion and needs a subscript, use brackets: \( \mathrm{Ca^{2+}} \) and \( \mathrm{NO_3^-} \) → \( \mathrm{Ca(NO_3)_2} \)
Example
Write the formula of the ionic compound formed between \( \mathrm{Na^+} \) and \( \mathrm{Cl^-} \).
▶️ Answer / Explanation
Charges: \( +1 \) and \( -1 \). They cancel in a 1:1 ratio.
Formula: \( \mathrm{NaCl} \)
Example
Write the formula for the compound formed between \( \mathrm{Ca^{2+}} \) and \( \mathrm{CO_3^{2-}} \).
▶️ Answer / Explanation
Charges: \( +2 \) and \( -2 \). Simplest ratio is 1:1.
Formula: \( \mathrm{CaCO_3} \)
Example
Write the formula of iron(III) sulfate.
(Iron(III) means \( \mathrm{Fe^{3+}} \); sulfate is \( \mathrm{SO_4^{2-}} \)).
▶️ Answer / Explanation
We need to balance charges:
\( \mathrm{Fe^{3+}} \) and \( \mathrm{SO_4^{2-}} \)
Lowest common multiple of 3 and 2 is 6.
- 2 sulfate ions give \( -4 \) charge — not enough
- 3 sulfate ions give \( -6 \) charge
- 2 iron(III) ions give \( +6 \) charge
Therefore the formula is: \[ \mathrm{Fe_2(SO_4)_3} \]
Writing Balanced Chemical & Ionic Equations
Chemical equations show reactants changing into products. Correct equations must be balanced, include charges where relevant, and (for ionic equations) must exclude spectator ions.
1. Balanced Chemical Equations
A balanced equation has the same number of each atom on both sides. Coefficients are adjusted; formulas must NOT be changed.
Steps: 1. Write correct formulas → 2. Balance atoms → 3. Check charges (if ions) → 4. Add state symbols

Example: \( \mathrm{2H_2 + O_2 \rightarrow 2H_2O} \)
2. State Symbols in Equations
| State Symbol | Meaning | Example |
|---|---|---|
| \( \mathrm{(s)} \) | solid | \( \mathrm{NaCl(s)} \) |
| \( \mathrm{(l)} \) | liquid | \( \mathrm{H_2O(l)} \) |
| \( \mathrm{(g)} \) | gas | \( \mathrm{CO_2(g)} \) |
| \( \mathrm{(aq)} \) | aqueous (dissolved in water) | \( \mathrm{Na^+(aq)} \) |
3. Ionic Equations (Without Spectator Ions)
Ionic equations show only the particles that take part in a reaction. Spectator ions (unchanged ions) are removed.
Steps: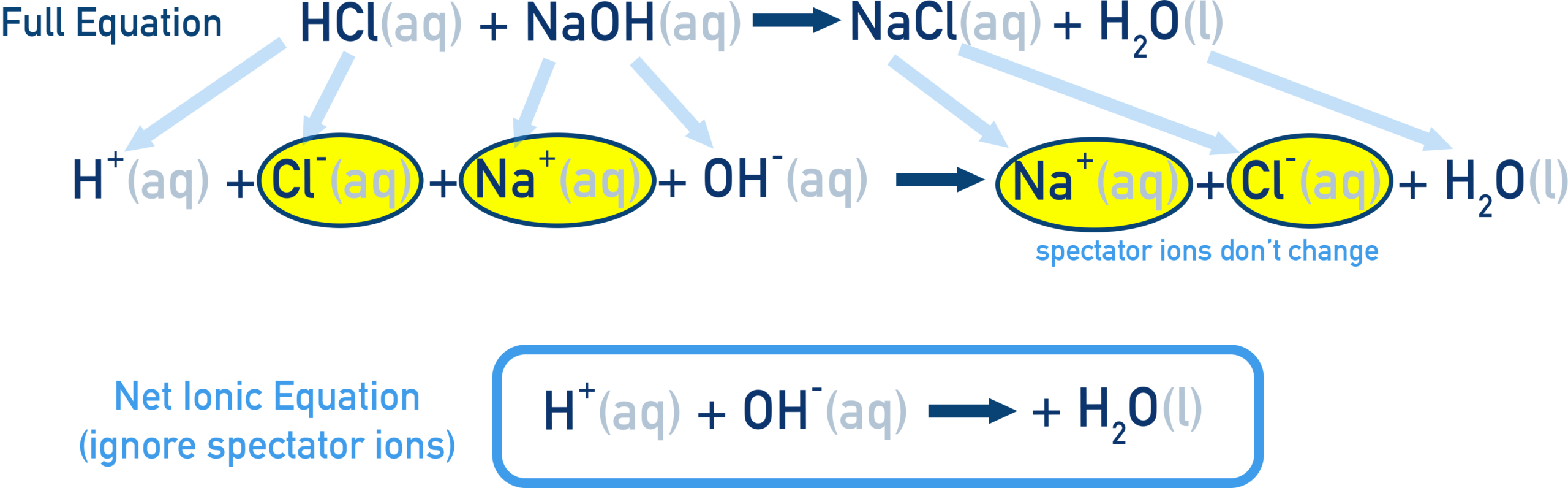
- Write full ionic form (split aqueous ionic compounds into ions).
- Remove spectator ions.
- Check balancing (atoms + charge).
Example (precipitation): \(\mathrm{Ba^{2+}(aq) + SO_4^{2-}(aq) \rightarrow BaSO_4(s)} \)
Example
Balance the equation for the reaction of magnesium with hydrochloric acid. Include state symbols.
▶️ Answer / Explanation
Unbalanced: \( \mathrm{Mg(s) + HCl(aq) \rightarrow MgCl_2(aq) + H_2(g)} \)
Balance HCl:
\( \mathrm{Mg(s) + 2HCl(aq) \rightarrow MgCl_2(aq) + H_2(g)} \)
Example
Write the ionic equation for the reaction between aqueous sodium hydroxide and copper(II) sulfate.
▶️ Answer / Explanation
Full ionic:
\( \mathrm{2OH^{-}(aq) + Cu^{2+}(aq) + SO_4^{2-}(aq) + 2Na^{+}(aq) \rightarrow Cu(OH)_2(s) + Na^{+}(aq) + SO_4^{2-}(aq)} \)
Remove spectator ions \(\mathrm{Na^+}\) and \(\mathrm{SO_4^{2-}}\):
\( \mathrm{Cu^{2+}(aq) + 2OH^{-}(aq) \rightarrow Cu(OH)_2(s)} \)
Example
Construct the ionic equation for the reaction between acidified dichromate(VI), \( \mathrm{Cr_2O_7^{2-}} \), and iron(II) ions, forming iron(III) ions and chromium(III) ions.
▶️ Answer / Explanation
Half-equations:
Reduction: \( \mathrm{Cr_2O_7^{2-} + 14H^{+} + 6e^{-} \rightarrow 2Cr^{3+} + 7H_2O} \)
Oxidation: \( \mathrm{Fe^{2+} \rightarrow Fe^{3+} + e^{-}} \)
Multiply the iron half-equation by 6 to balance electrons:
\( \mathrm{6Fe^{2+} \rightarrow 6Fe^{3+} + 6e^{-}} \)
Combine:
\( \mathrm{Cr_2O_7^{2-} + 14H^{+} + 6Fe^{2+} \rightarrow 2Cr^{3+} + 6Fe^{3+} + 7H_2O} \)
Empirical and Molecular Formulae
Chemical formulas describe the composition of a substance. Two key types of formulas are the empirical formula and the molecular formula.
Empirical Formula![]()
- The simplest whole-number ratio of atoms of each element in a compound.
- Does not give the actual number of atoms in a molecule, only the simplest ratio.
- Example: The empirical formula of glucose \( \mathrm{C_6H_{12}O_6} \) is \( \mathrm{CH_2O} \).
Molecular Formula
- The actual number of atoms of each element in one molecule of a compound.
- It is a whole-number multiple of the empirical formula.
- Example: Glucose has the molecular formula \( \mathrm{C_6H_{12}O_6} \).
Relationship Between Empirical and Molecular Formula
\( \text{Molecular formula} = n \times \text{Empirical formula} \)
Where \( n = \dfrac{\text{Mr of molecule}}{\text{Mr of empirical formula}} \)
Example
State the difference between an empirical formula and a molecular formula.
▶️ Answer / Explanation
The empirical formula shows the simplest whole-number ratio of elements. The molecular formula shows the actual number of atoms in a molecule.
Example
A compound has the empirical formula \( \mathrm{CH_2} \) and a relative molecular mass of 56. Find its molecular formula.
▶️ Answer / Explanation
Empirical formula Mr = \( \mathrm{C} (12) + 2\mathrm{H} (2) = 14 \)
\( n = \dfrac{56}{14} = 4 \)
Molecular formula = \( 4 \times \mathrm{CH_2} = \mathrm{C_4H_8} \)
Example
A compound contains 52.2% carbon, 13.0% hydrogen and 34.8% oxygen. Its relative molecular mass is 46. Determine its empirical and molecular formulas.
▶️ Answer / Explanation
Step 1: Convert percentages to moles
C: \( \dfrac{52.2}{12} = 4.35 \)
H: \( \dfrac{13.0}{1} = 13.0 \)
O: \( \dfrac{34.8}{16} = 2.175 \)
Step 2: Divide by the smallest value
C: \( \dfrac{4.35}{2.175} = 2 \)
H: \( \dfrac{13.0}{2.175} = 6 \)
O: \( \dfrac{2.175}{2.175} = 1 \)
Empirical formula = \( \mathrm{C_2H_6O} \)
Step 3: Compare with molecular mass
Mr of \( \mathrm{C_2H_6O} \) = \( 46 \)
Given Mr = \( 46 \Rightarrow n = 1 \)
Molecular formula = \( \mathrm{C_2H_6O} \)
Anhydrous, Hydrated and Water of Crystallisation
Some ionic compounds contain water molecules within their solid crystal structure. These water molecules are chemically bound and are part of the formula.
Hydrated Compounds
A hydrated compound contains water of crystallisation chemically bonded within its structure.
- Its formula includes water molecules, written as \( \mathrm{nH_2O} \).
- Example: \( \mathrm{CuSO_4\cdot5H_2O} \) (hydrated copper(II) sulfate).
Anhydrous Compounds
An anhydrous compound contains no water of crystallisation.

- Formed when a hydrated salt is heated and loses its water.
- Example: \( \mathrm{CuSO_4} \) (anhydrous copper(II) sulfate).
Water of Crystallisation
These are the fixed number of water molecules chemically bound inside a salt’s lattice.
- They are not simply trapped water; they are required for the crystal structure.
- Removed by heating, leaving an anhydrous salt.
General Form
Hydrated salt: \( \mathrm{Salt\cdot nH_2O} \)
Anhydrous salt: \( \mathrm{Salt} \)
When heated: \( \mathrm{Salt\cdot nH_2O \rightarrow Salt + nH_2O} \)
Example
State the meaning of the term anhydrous.
▶️ Answer / Explanation
Anhydrous means a substance contains no water of crystallisation in its structure.
Example
Write the formula for hydrated magnesium sulfate containing 7 water molecules.
▶️ Answer / Explanation
The formula is \( \mathrm{MgSO_4\cdot7H_2O} \).
Example
A sample of hydrated salt \( \mathrm{CuSO_4\cdot nH_2O} \) is heated. Its mass decreases from \( 3.20\,\mathrm{g} \) to \( 2.00\,\mathrm{g} \). Determine the value of \( n \).
▶️ Answer / Explanation
Mass of water lost: \( 3.20 – 2.00 = 1.20\,\mathrm{g} \)
Moles of anhydrous \( \mathrm{CuSO_4} \): Mr = 159.5 \( n = \dfrac{2.00}{159.5} = 0.01254\,\mathrm{mol} \)
Moles of water lost: Mr of \( \mathrm{H_2O} = 18 \) \( n = \dfrac{1.20}{18} = 0.06667\,\mathrm{mol} \)
Ratio: \( \dfrac{0.06667}{0.01254} = 5.31 \approx 5 \)
Therefore: \( n = 5 \)
Formula = \( \mathrm{CuSO_4\cdot5H_2O} \)
Calculating Empirical and Molecular Formulae
Empirical and molecular formulas can be calculated from percentage composition, mass data, or from molar masses. The process always involves converting masses to moles and finding the simplest ratio.
Steps to Calculate Empirical Formula
- Write down mass or percentage of each element.
- Convert each to moles using \( \text{moles} = \dfrac{\text{mass}}{\mathrm{Ar}} \).
- Divide all mole values by the smallest value.
- Round to nearest whole numbers (multiply all by 2 or 3 if necessary).
- Write the empirical formula.
Steps to Calculate Molecular Formula
\( n = \dfrac{\mathrm{M_r\ of\ molecule}}{\mathrm{M_r\ of\ empirical\ formula}} \)
Then: \( \text{Molecular formula} = n \times \text{Empirical formula} \)
Example
A compound contains 75% carbon and 25% hydrogen by mass. Find the empirical formula.
▶️ Answer / Explanation
Assume 100 g sample:
C: \( 75\,\mathrm{g} \rightarrow \dfrac{75}{12} = 6.25\,\mathrm{mol} \)
H: \( 25\,\mathrm{g} \rightarrow \dfrac{25}{1} = 25\,\mathrm{mol} \)
Divide by smallest value:
C: \( \dfrac{6.25}{6.25} = 1 \)
H: \( \dfrac{25}{6.25} = 4 \)
Empirical formula = \( \mathrm{CH_4} \)
Example
A sample contains \( 4.2\,\mathrm{g} \) of nitrogen and \( 12.0\,\mathrm{g} \) of oxygen. Find the empirical formula.
▶️ Answer / Explanation
N: \( \dfrac{4.2}{14} = 0.30\,\mathrm{mol} \)
O: \( \dfrac{12.0}{16} = 0.75\,\mathrm{mol} \)
Divide by smallest value:
N: \( \dfrac{0.30}{0.30} = 1 \)
O: \( \dfrac{0.75}{0.30} = 2.5 \)
Multiply all by 2 to get whole numbers:
N : 2, O : 5
Empirical formula = \( \mathrm{N_2O_5} \)
Example
A hydrocarbon contains 82.76% carbon and 17.24% hydrogen by mass. Its relative molecular mass is \( 58 \). Calculate the empirical and molecular formulas.
▶️ Answer / Explanation
Step 1: Convert to moles
C: \( \dfrac{82.76}{12} = 6.896\,\mathrm{mol} \)
H: \( \dfrac{17.24}{1} = 17.24\,\mathrm{mol} \)
Step 2: Divide by smallest value
C: \( \dfrac{6.896}{6.896} = 1 \)
H: \( \dfrac{17.24}{6.896} = 2.50 \)
Multiply both by 2:
C = 2, H = 5
Empirical formula = \( \mathrm{C_2H_5} \)
Step 3: Calculate molecular formula
Mr of empirical formula \( \mathrm{C_2H_5} = 29 \)
\( n = \dfrac{58}{29} = 2 \)
Molecular formula = \( \mathrm{C_4H_{10}} \)
