CIE AS/A Level Chemistry 2.4 Reacting masses and volumes (of solutions and gases) Study Notes- 2025-2027 Syllabus
CIE AS/A Level Chemistry 2.4 Reacting masses and volumes (of solutions and gases) Study Notes – New Syllabus
CIE AS/A Level Chemistry 2.4 Reacting masses and volumes (of solutions and gases) Study Notes at IITian Academy focus on specific topic and type of questions asked in actual exam. Study Notes focus on AS/A Level Chemistry latest syllabus with Candidates should be able to:
- perform calculations including use of the mole concept, involving:
(a) reacting masses (from formulas and equations) including percentage yield calculations
(b) volumes of gases (e.g. in the burning of hydrocarbons)
(c) volumes and concentrations of solutions
(d) limiting reagent and excess reagent (When performing calculations, candidates’ answers should reflect the number of significant figures given or asked for in the question. When rounding up or down, candidates should ensure that significant figures are neither lost unnecessarily nor used beyond what is justified (see also Mathematical requirements section).)
(e) deduce stoichiometric relationships from calculations such as those in 2.4.1(a)–(d)
Mole Calculations — Reacting Masses & Percentage Yield
Reacting mass calculations use balanced chemical equations to convert between the mass of one substance and the mass of another using moles. Percentage yield calculations compare the actual yield to the theoretical yield.
1. Reacting Mass Calculations
All reacting mass calculations follow the same pattern:
- Write a balanced equation
- Convert mass to moles using \( n = \dfrac{m}{\mathrm{M_r}} \)
- Use mole ratio from the balanced equation
- Convert moles back to mass using \( m = n \times \mathrm{M_r} \)
Important: Answers must be given to an appropriate number of significant figures, based on the data provided in the question.
2. Percentage Yield
\( \text{Percentage yield} = \dfrac{\text{actual yield}}{\text{theoretical yield}} \times 100\% \)
- Actual yield = mass obtained in experiment.
- Theoretical yield = calculated mass from reacting mass calculations.
- Percentage yield cannot exceed \( 100\% \).
Example
What mass of water is formed when \( 4.0\,\mathrm{g} \) of hydrogen reacts with oxygen?
Balanced equation: \( \mathrm{2H_2 + O_2 \rightarrow 2H_2O} \)
▶️ Answer / Explanation
\( \mathrm{M_r(H_2)} = 2 \)
Moles of \( \mathrm{H_2} \): \( n = \dfrac{4.0}{2} = 2.0\,\mathrm{mol} \)
Ratio \( \mathrm{H_2 : H_2O} = 1:1 \)
Moles of \( \mathrm{H_2O} = 2.0\,\mathrm{mol} \)
\( \mathrm{M_r(H_2O)} = 18 \)
Mass: \( m = 2.0 \times 18 = 36\,\mathrm{g} \)
Answer: \( 36\,\mathrm{g} \) (2 significant figures → matches data)
Example
\( 10.0\,\mathrm{g} \) of calcium carbonate reacts with \( 8.0\,\mathrm{g} \) of hydrochloric acid. Calculate the mass of carbon dioxide formed.
Balanced equation: \( \mathrm{CaCO_3 + 2HCl \rightarrow CaCl_2 + H_2O + CO_2} \)
▶️ Answer / Explanation
Step 1: Moles of each reactant
\( \mathrm{M_r(CaCO_3)} = 100 \)
Moles \( \mathrm{CaCO_3} = \dfrac{10.0}{100} = 0.100\,\mathrm{mol} \)
\( \mathrm{M_r(HCl)} = 36.5 \)
Moles \( \mathrm{HCl} = \dfrac{8.0}{36.5} = 0.219\,\mathrm{mol} \)
Step 2: Identify limiting reagent
Equation needs \( 2\,\mathrm{mol} \) HCl per \( 1\,\mathrm{mol} \) CaCO\(_3\).
Moles HCl needed for \( 0.100\,\mathrm{mol} \) CaCO\(_3\) = \( 0.200\,\mathrm{mol} \).
Available HCl = \( 0.219\,\mathrm{mol} \) → excess.
Limiting reagent = CaCO\(_3\).
Step 3: Moles of CO\(_2\)
Ratio \( \mathrm{CaCO_3 : CO_2} = 1 : 1 \)
Moles \( \mathrm{CO_2} = 0.100\,\mathrm{mol} \)
Step 4: Mass of CO\(_2\)
\( \mathrm{M_r(CO_2)} = 44 \)
Mass \( = 0.100 \times 44 = 4.4\,\mathrm{g} \)
Answer: \( 4.4\,\mathrm{g} \) (2 s.f.)
Example
Ethanol is produced by the fermentation reaction: \( \mathrm{C_6H_{12}O_6 \rightarrow 2C_2H_5OH + 2CO_2} \)
If \( 180\,\mathrm{g} \) of glucose produces \( 70.0\,\mathrm{g} \) of ethanol, calculate the percentage yield.
▶️ Answer / Explanation
Step 1: Moles of glucose
\( \mathrm{M_r(glucose)} = 180 \)
Moles = \( \dfrac{180}{180} = 1.00\,\mathrm{mol} \)
Step 2: Moles of ethanol theoretically produced
Ratio: \( \mathrm{1\ mol\ glucose : 2\ mol\ ethanol} \)
Moles ethanol (theoretical) = \( 2.00\,\mathrm{mol} \)
Step 3: Convert to mass
\( \mathrm{M_r(C_2H_5OH)} = 46 \)
Theoretical mass = \( 2.00 \times 46 = 92\,\mathrm{g} \)
Step 4: Percentage yield
\( \text{Percentage yield} = \dfrac{70.0}{92} \times 100 = 76.1\% \)
Answer: \( 76.1\% \) (3 s.f., matching 70.0 g)
Mole Calculations — Gas Volumes
Gas volume calculations use the mole concept together with molar volume relationships. For reactions involving gases (e.g., combustion of hydrocarbons), balanced equations give mole ratios, which can be converted into gas volumes.
1. Molar Volume of a Gas 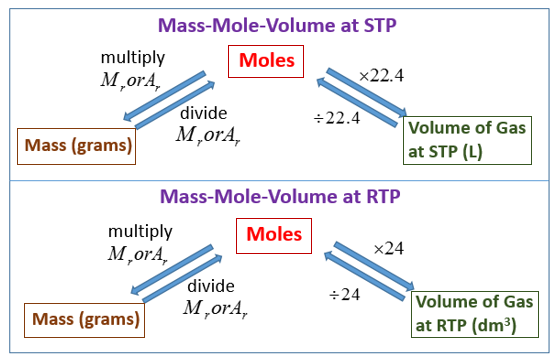
At room temperature and pressure (rtp):
\( 1\,\mathrm{mol} \text{ of any gas occupies } 24\,\mathrm{dm^3} \)
Gas volume \( = n \times 24\,\mathrm{dm^3} \)
Moles \( = \dfrac{\text{gas volume}}{24\,\mathrm{dm^3}} \)
This molar volume is independent of the identity of the gas (all gases behave similarly at rtp).
2. Combustion of Hydrocarbons
Hydrocarbons burn in oxygen to form carbon dioxide and water:
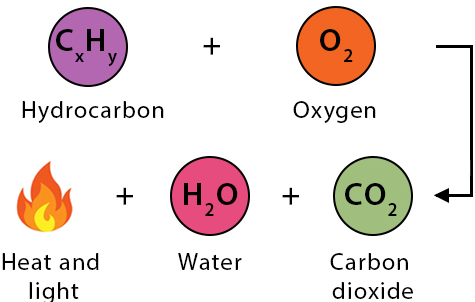
\( \mathrm{C_{x}H_{y} + O_{2} \rightarrow CO_{2} + H_{2}O} \)
- Use mole ratios from the equation to convert between volumes of reactant and product gases.
- Only gases count toward gas volume calculations.
- Water is gas only at high temperatures; at rtp, it is liquid.
3. Steps for Gas Volume Calculations
- Write a balanced equation.
- Use mole ratios from the equation.
- Use molar volume \( 24\,\mathrm{dm^3\,mol^{-1}} \) to convert moles ↔ volumes.
- Give answers to appropriate significant figures.
Example
What volume is occupied by \( 0.50\,\mathrm{mol} \) of oxygen gas at rtp?
▶️ Answer / Explanation
Volume \( = n \times 24 = 0.50 \times 24 = 12\,\mathrm{dm^3} \)
Answer: \( 12\,\mathrm{dm^3} \) (2 s.f.)
Example
Propane burns in oxygen according to the equation: \( \mathrm{C_3H_8 + 5O_2 \rightarrow 3CO_2 + 4H_2O} \)
What volume of oxygen is required to completely burn \( 2.0\,\mathrm{dm^3} \) of propane gas at rtp?
▶️ Answer / Explanation
Mole ratio \( \mathrm{C_3H_8 : O_2} = 1 : 5 \)
Gas volumes at same conditions follow the same ratio.
Volume of \( \mathrm{O_2} = 2.0 \times 5 = 10.0\,\mathrm{dm^3} \)
Answer: \( 10.0\,\mathrm{dm^3} \) (3 s.f.)
Example
Zinc reacts with hydrochloric acid to produce hydrogen gas: \( \mathrm{Zn + 2HCl \rightarrow ZnCl_2 + H_2} \)
What volume of hydrogen gas (at rtp) is produced from \( 6.5\,\mathrm{g} \) of zinc?
▶️ Answer / Explanation
Step 1: Moles of zinc
\( \mathrm{M_r(Zn)} = 65 \)
Moles \( = \dfrac{6.5}{65} = 0.100\,\mathrm{mol} \)
Step 2: Mole ratio
\( \mathrm{Zn : H_2} = 1 : 1 \)
Moles of \( \mathrm{H_2} = 0.100\,\mathrm{mol} \)
Step 3: Convert to gas volume
Volume \( = 0.100 \times 24 = 2.4\,\mathrm{dm^3} \)
Answer: \( 2.4\,\mathrm{dm^3} \) (2 s.f.)
Mole Calculations — Volumes and Concentrations of Solutions
Solutions contain solutes dissolved in a solvent. Their concentration describes how much solute is present per unit volume. The mole concept links mass, moles, concentration and solution volume.
Key Equations for Solutions
Moles: \( n = C \times V \)
Where: \( n = \) moles, \( C = \) concentration in \( \mathrm{mol\,dm^{-3}} \), \( V = \) volume in \( \mathrm{dm^{3}} \)
Important: If volume is in \( \mathrm{cm^{3}} \), convert to \( \mathrm{dm^{3}} \):
\( \mathrm{1\,dm^{3} = 1000\,cm^{3}} \)
\( V\,(\mathrm{dm^{3}}) = \dfrac{V\,(\mathrm{cm^{3}})}{1000} \)
Using Concentration in Stoichiometric Calculations
Balanced equations give mole ratios. Solution concentrations allow us to calculate unknown volumes or concentrations of reactants or products.
Steps:
- Use equation \( n = C \times V \)
- Apply mole ratio from balanced equation
- Convert moles back to required quantity (mass, volume, concentration)
Titration-Type Calculations
Acid–base and redox titrations frequently involve concentration–volume–mole relationships.
General neutralisation equation: \( \mathrm{acid + base \rightarrow salt + water} \)
Example
What amount of substance is present in \( 25.0\,\mathrm{cm^{3}} \) of a \( 0.200\,\mathrm{mol\,dm^{-3}} \) solution of sodium hydroxide?
▶️ Answer / Explanation
Convert volume:
\( V = \dfrac{25.0}{1000} = 0.0250\,\mathrm{dm^{3}} \)
Use \( n = C \times V \):
\( n = 0.200 \times 0.0250 = 0.00500\,\mathrm{mol} \)
Answer: \( 5.00\times10^{-3}\,\mathrm{mol} \) (3 s.f.)
Example
\( 25.0\,\mathrm{cm^{3}} \) of sulfuric acid reacts exactly with \( 30.0\,\mathrm{cm^{3}} \) of \( 0.150\,\mathrm{mol\,dm^{-3}} \) sodium hydroxide.
Equation: \( \mathrm{H_2SO_4 + 2NaOH \rightarrow Na_2SO_4 + 2H_2O} \)
Calculate the concentration of the sulfuric acid.
▶️ Answer / Explanation
Step 1: Moles of NaOH
\( V = \dfrac{30.0}{1000} = 0.0300\,\mathrm{dm^{3}} \)
\( n = 0.150 \times 0.0300 = 0.00450\,\mathrm{mol} \)
Step 2: Mole ratio
\( \mathrm{2NaOH : H_2SO_4} = 2 : 1 \)
Moles of \( \mathrm{H_2SO_4} = \dfrac{0.00450}{2} = 0.00225\,\mathrm{mol} \)
Step 3: Find concentration
Volume of acid \( = \dfrac{25.0}{1000} = 0.0250\,\mathrm{dm^{3}} \)
\( C = \dfrac{n}{V} = \dfrac{0.00225}{0.0250} = 0.0900\,\mathrm{mol\,dm^{-3}} \)
Answer: \( 0.0900\,\mathrm{mol\,dm^{-3}} \) (3 s.f.)
Example
\( 25.0\,\mathrm{cm^{3}} \) of a sodium carbonate solution reacts completely with \( 35.0\,\mathrm{cm^{3}} \) of \( 0.200\,\mathrm{mol\,dm^{-3}} \) hydrochloric acid.
Equation: \( \mathrm{Na_2CO_3 + 2HCl \rightarrow 2NaCl + H_2O + CO_2} \)
Calculate the concentration of the sodium carbonate solution.
▶️ Answer / Explanation
Step 1: Moles of HCl
\( V = \dfrac{35.0}{1000} = 0.0350\,\mathrm{dm^{3}} \)
\( n = 0.200 \times 0.0350 = 0.00700\,\mathrm{mol} \)
Step 2: Mole ratio
\( \mathrm{2HCl : Na_2CO_3} = 2 : 1 \)
Moles of sodium carbonate \( = \dfrac{0.00700}{2} = 0.00350\,\mathrm{mol} \)
Step 3: Concentration of sodium carbonate
Volume of \( \mathrm{Na_2CO_3} = \dfrac{25.0}{1000} = 0.0250\,\mathrm{dm^{3}} \)
\( C = \dfrac{0.00350}{0.0250} = 0.140\,\mathrm{mol\,dm^{-3}} \)
Answer: \( 0.140\,\mathrm{mol\,dm^{-3}} \) (3 s.f.)
Limiting Reagent and Excess Reagent
In a reaction with more than one reactant, the limiting reagent is the reactant that is completely used up first. It determines the amount of product formed. Any reactant present in more than the required amount is the excess reagent.
What Is the Limiting Reagent?
- The limiting reagent produces the smallest amount of product.

- It is completely consumed during the reaction.
- When it runs out, the reaction stops.
Excess reagent: any reactant that remains after the reaction has finished.
How to Identify the Limiting Reagent
- Write a balanced equation
- Convert masses or volumes to moles
- Use the mole ratio in the balanced equation
- Compare the available moles with the required moles
- The reactant that produces fewer moles of product is the limiting reagent
All answers should use appropriate significant figures, matching the data in the question.
Why It Matters
- The limiting reagent determines the maximum theoretical yield.
- You cannot calculate percentage yield until the limiting reagent is identified.
- Industrial processes use limiting reagent calculations to reduce waste and cost.
Example
Hydrogen reacts with chlorine: \( \mathrm{H_2 + Cl_2 \rightarrow 2HCl} \)
If \( 0.40\,\mathrm{mol} \) of \( \mathrm{H_2} \) reacts with \( 0.25\,\mathrm{mol} \) of \( \mathrm{Cl_2} \), identify the limiting reagent.
▶️ Answer / Explanation
Mole ratio \( \mathrm{H_2 : Cl_2} = 1 : 1 \)
We need equal moles, but we have:
\( \mathrm{H_2 = 0.40\,mol} \)
\( \mathrm{Cl_2 = 0.25\,mol} \)
Limiting reagent = \( \mathrm{Cl_2} \)
Example
Aluminium reacts with chlorine gas: \( \mathrm{2Al + 3Cl_2 \rightarrow 2AlCl_3} \)
If \( 5.40\,\mathrm{g} \) of aluminium reacts with \( 10.0\,\mathrm{g} \) of chlorine, find the limiting reagent.
▶️ Answer / Explanation
Step 1: Convert to moles
\( \mathrm{M_r(Al)} = 27 \)
\( n_{\mathrm{Al}} = \dfrac{5.40}{27} = 0.200\,\mathrm{mol} \)
\( \mathrm{M_r(Cl_2)} = 71 \)
\( n_{\mathrm{Cl_2}} = \dfrac{10.0}{71} = 0.141\,\mathrm{mol} \)
Step 2: Use mole ratio
Ratio required: \( \mathrm{Al : Cl_2 = 2 : 3} \)
For \( 0.200\,\mathrm{mol} \) of Al, required \( \mathrm{Cl_2} = 0.300\,\mathrm{mol} \)
But only \( 0.141\,\mathrm{mol} \) available → insufficient.
Limiting reagent = \( \mathrm{Cl_2} \)
Example
Magnesium reacts with nitric acid: \( \mathrm{Mg + 2HNO_3 \rightarrow Mg(NO_3)_2 + H_2} \)
If \( 6.00\,\mathrm{g} \) of \( \mathrm{Mg} \) reacts with \( 8.00\,\mathrm{g} \) of \( \mathrm{HNO_3} \), calculate:
- The limiting reagent
- The mass of hydrogen produced
▶️ Answer / Explanation
Step 1: Moles of reactants
\( \mathrm{M_r(Mg)} = 24 \)
\( n_{\mathrm{Mg}} = \dfrac{6.00}{24} = 0.250\,\mathrm{mol} \)
\( \mathrm{M_r(HNO_3)} = 63 \)
\( n_{\mathrm{HNO_3}} = \dfrac{8.00}{63} = 0.127\,\mathrm{mol} \)
Step 2: Use mole ratio (Mg : HNO\(_3\) = 1 : 2)
For \( 0.250\,\mathrm{mol} \) Mg → required \( 0.500\,\mathrm{mol} \) HNO\(_3\)
Available = \( 0.127\,\mathrm{mol} \) → insufficient
Limiting reagent = \( \mathrm{HNO_3} \)
Step 3: Moles of product hydrogen
Ratio: \( \mathrm{2HNO_3 : H_2} = 2 : 1 \)
Moles \( \mathrm{H_2} = \dfrac{0.127}{2} = 0.0635\,\mathrm{mol} \)
Step 4: Mass of hydrogen
\( \mathrm{M_r(H_2)} = 2 \)
Mass = \( 0.0635 \times 2 = 0.127\,\mathrm{g} \)
Answer: Limiting reagent = \( \mathrm{HNO_3} \) Mass of hydrogen = \( 0.127\,\mathrm{g} \) (3 s.f.)
Deducing Stoichiometric Relationships from Calculations
Stoichiometry describes the quantitative relationships between reactants and products in a chemical reaction. Even if an equation is not given, you can deduce stoichiometric ratios using mole, mass, gas volume or concentration data.
What Is a Stoichiometric Relationship?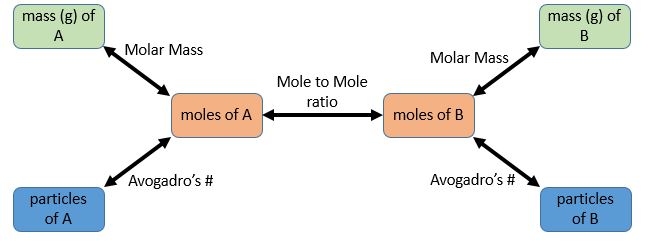
- It is the mole ratio between reactants and products.
- Ratios can be deduced from reacting masses, gas volumes, or solution data.
- Stoichiometric coefficients in equations reflect these mole ratios.
Example:
\( \mathrm{2H_2 + O_2 \rightarrow 2H_2O} \)
→ stoichiometric ratio \( \mathrm{H_2 : O_2} = 2 : 1 \)
How to Deduce Stoichiometric Ratios
From any quantitative data:
- Convert all masses, gas volumes or solution quantities into moles.
- Divide by the smallest number of moles to get a simplest whole-number ratio.
- These ratios correspond to coefficients in the balanced chemical equation.
- Significant figures should match the precision of the given data.
Useful Relationships for Deducing Stoichiometry
Mass \(\rightarrow\) moles: \( n = \dfrac{m}{\mathrm{M_r}} \)
Gas volume \(\rightarrow\) moles: \( n = \dfrac{V}{24\,\mathrm{dm^3}} \)
Solution concentration \(\rightarrow\) moles: \( n = C \times V \)
Example
When \( 4.0\,\mathrm{g} \) of hydrogen reacts, it forms \( 36\,\mathrm{g} \) of water. Deduce the mole ratio between hydrogen and water.
▶️ Answer / Explanation
Moles of \( \mathrm{H_2} = \dfrac{4.0}{2} = 2.0 \)
Moles of \( \mathrm{H_2O} = \dfrac{36}{18} = 2.0 \)
Divide by smallest value:
Ratio = \( 2.0 : 2.0 = 1 : 1 \)
Stoichiometric relationship: \( \mathrm{H_2 : H_2O = 1 : 1} \)
Example
In a reaction, \( 5.60\,\mathrm{g} \) of nitrogen reacts with \( 3.20\,\mathrm{g} \) of hydrogen to form ammonia. Deduce the balanced equation.
▶️ Answer / Explanation
Moles \( \mathrm{N_2} = \dfrac{5.60}{28} = 0.200 \)
Moles \( \mathrm{H_2} = \dfrac{3.20}{2} = 1.60 \)
Divide by smallest value:
N\(_2\): \( \dfrac{0.200}{0.200} = 1 \)
H\(_2\): \( \dfrac{1.60}{0.200} = 8 \)
So ratio \( \mathrm{N_2 : H_2 = 1 : 8} \)
But in the known reaction, hydrogen appears as \( \mathrm{3H_2} \). This ratio simplifies to \( 1 : 3 \) after correcting (because nitrogen and hydrogen react as molecules).
Balanced equation:
\( \mathrm{N_2 + 3H_2 \rightarrow 2NH_3} \)
Example
In a reaction, \( 4.8\,\mathrm{dm^3} \) of sulfur dioxide reacts completely with \( 3.6\,\mathrm{g} \) of oxygen to form sulfur trioxide.
Deduce the balanced chemical equation.
▶️ Answer / Explanation
Step 1: Convert all to moles
Moles \( \mathrm{SO_2} = \dfrac{4.8}{24} = 0.200 \)
\( \mathrm{M_r(O_2)} = 32 \)
Moles \( \mathrm{O_2} = \dfrac{3.6}{32} = 0.1125 \)
Step 2: Divide by smallest value
\( \mathrm{SO_2} = \dfrac{0.200}{0.1125} = 1.78 \)
\( \mathrm{O_2} = \dfrac{0.1125}{0.1125} = 1 \)
Multiply both by 2 to clear decimals → \( 3.56 : 2 \)\ Multiply by 1.5 → approximately \( 5.34 : 3 \)\ Round to simplest whole ratio \( \approx 2 : 1 \)
Step 3: Write balanced equation
\( \mathrm{2SO_2 + O_2 \rightarrow 2SO_3} \)
Final Answer: \( \mathrm{2SO_2 + O_2 \rightarrow 2SO_3} \)
