CIE AS/A Level Chemistry 23.1 Lattice energy and Born-Haber cycles Study Notes- 2025-2027 Syllabus
CIE AS/A Level Chemistry 23.1 Lattice energy and Born-Haber cycles Study Notes – New Syllabus
CIE AS/A Level Chemistry 23.1 Lattice energy and Born-Haber cycles Study Notes at IITian Academy focus on specific topic and type of questions asked in actual exam. Study Notes focus on AS/A Level Chemistry latest syllabus with Candidates should be able to:
define and use the terms:
(a) enthalpy change of atomisation, ΔHₐₜ
(b) lattice energy, ΔHₗₐₜₜ (the change from gas phase ions to solid lattice)(a) define and use the term first electron affinity, EA
(b) explain the factors affecting the electron affinities of elements
(c) describe and explain the trends in the electron affinities of the Group 16 and Group 17 elementsconstruct and use Born–Haber cycles for ionic solids
(limited to +1 and +2 cations, –1 and –2 anions)carry out calculations involving Born–Haber cycles
explain, in qualitative terms, the effect of ionic charge and of ionic radius on the numerical magnitude of a lattice energy
Enthalpy Changes: Definitions and Use
Certain standard enthalpy changes are used to describe energy changes in chemical reactions. 
(a) Enthalpy Change of Atomisation, \( \mathrm{\Delta H_{at}} \)
The enthalpy change of atomisation is defined as the enthalpy change when one mole of gaseous atoms is formed from the element in its standard state.
This enthalpy change is always endothermic.
Example equation: \( \mathrm{\tfrac{1}{2}Cl_2(g) \rightarrow Cl(g)} \)
For elements that are already monatomic gases, the enthalpy change of atomisation is zero.
(b) Lattice Energy, \( \mathrm{\Delta H_{latt}} \)
Lattice energy is defined as the enthalpy change when one mole of an ionic solid is formed from its gaseous ions.
This definition refers to the change from gas phase ions to a solid ionic lattice.
Lattice energy is always exothermic.
Example equation: \( \mathrm{Na^+(g) + Cl^-(g) \rightarrow NaCl(s)} \)
Example
Write an equation to represent the enthalpy change of atomisation of magnesium.
▶️ Answer / Explanation
The standard state of magnesium is solid magnesium.
One mole of gaseous magnesium atoms must be formed.
The correct equation is:
\( \mathrm{Mg(s) \rightarrow Mg(g)} \)
Example
Explain why lattice energy for magnesium oxide is more exothermic than for sodium chloride.
▶️ Answer / Explanation
Magnesium oxide contains ions with higher charges, \( \mathrm{Mg^{2+}} \) and \( \mathrm{O^{2-}} \).
The electrostatic attraction between oppositely charged ions is stronger.
Stronger attractions release more energy when the lattice forms.
Electron Affinity
Electron affinity is an important enthalpy change used to describe the tendency of atoms to gain electrons. Accurate definitions and explanations are required at AS Level.
(a) First Electron Affinity, \( \mathrm{EA} \)
The first electron affinity is defined as the enthalpy change when one mole of gaseous atoms each gains one electron to form one mole of gaseous 1⁻ ions.

Example equation: \( \mathrm{X(g) + e^- \rightarrow X^-(g)} \)
First electron affinity is usually exothermic.
(b) Factors Affecting Electron Affinity
- Nuclear charge – greater nuclear charge increases attraction for the incoming electron
- Atomic radius – larger atoms have weaker attraction for an extra electron
- Shielding – inner-shell electrons reduce nuclear attraction
- Electron–electron repulsion – repulsion in occupied orbitals reduces electron affinity
- Subshell structure – half-filled and full subshells are more stable
(c) Trends in Electron Affinity of Group 16 and Group 17
Group 17 (Halogens):
Electron affinity becomes less exothermic down the group.
- Atomic radius increases down the group
- Increased shielding reduces attraction for the incoming electron
Fluorine has a less exothermic electron affinity than chlorine.
Fluorine is very small, so electron–electron repulsion in the compact 2p orbital reduces the energy released.
Group 16 (Chalcogens):
Electron affinity is less exothermic than Group 17 elements in the same period.
- Group 16 atoms already have paired electrons in p orbitals
- Incoming electrons experience increased electron–electron repulsion
Example
Write an equation to represent the first electron affinity of oxygen.
▶️ Answer / Explanation
Oxygen gains one electron in the gaseous state.
The correct equation is:
\( \mathrm{O(g) + e^- \rightarrow O^-(g)} \)
Example
Explain why chlorine has a more exothermic first electron affinity than fluorine.
▶️ Answer / Explanation
Fluorine atoms are very small.
The incoming electron enters a compact 2p orbital.
There is significant electron–electron repulsion.
In chlorine, the larger 3p orbital reduces repulsion, so more energy is released.
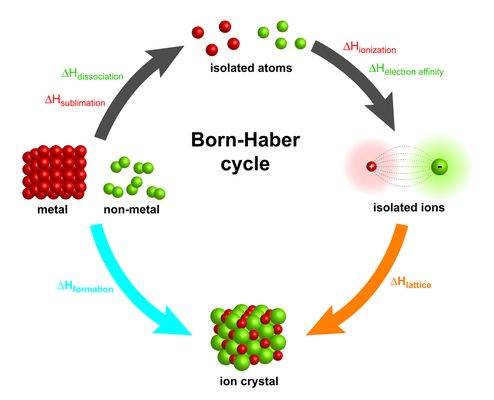
Born–Haber Cycles for Ionic Solids
A Born–Haber cycle is an energy cycle that uses Hess’s Law to calculate the lattice energy of an ionic compound or another enthalpy change that cannot be measured directly.
Purpose of a Born–Haber Cycle
- To calculate lattice energy
- To analyse the energetic stability of ionic solids
- To apply Hess’s Law using known enthalpy changes
Enthalpy Changes Used in Born–Haber Cycles
- Standard enthalpy of formation
- Enthalpy change of atomisation
- Ionisation energies of metals
- Electron affinities of non-metals
- Lattice energy
Constructing a Born–Haber Cycle
- Start with the elements in their standard states

- Convert elements into gaseous atoms
- Form gaseous ions using ionisation energies and electron affinities
- Combine gaseous ions to form the ionic lattice
- Apply Hess’s Law to relate these steps to the enthalpy of formation
For compounds containing \( \mathrm{M^+} \), \( \mathrm{M^{2+}} \), \( \mathrm{X^-} \) or \( \mathrm{X^{2-}} \), the appropriate number of ionisation energies and electron affinities must be included.
Using a Born–Haber Cycle
Hess’s Law is applied by equating the sum of enthalpy changes around the cycle. The lattice energy is then calculated algebraically.
Example
A Born–Haber cycle is used to calculate the lattice energy of sodium chloride. State two enthalpy changes, other than lattice energy, that must be included in the cycle.
▶️ Answer / Explanation
Examples include:
• Enthalpy of formation of sodium chloride
• Enthalpy change of atomisation of sodium
• First ionisation energy of sodium
• First electron affinity of chlorine
Example
The following data are given for magnesium oxide:
\( \mathrm{\Delta H_f^\circ(MgO) = -602\ kJ\,mol^{-1}} \)
\( \mathrm{\Delta H_{at}(Mg) = +150\ kJ\,mol^{-1}} \)
\( \mathrm{IE_1(Mg) = +738\ kJ\,mol^{-1}} \)
\( \mathrm{IE_2(Mg) = +1451\ kJ\,mol^{-1}} \)
\( \mathrm{\Delta H_{at}(O) = +249\ kJ\,mol^{-1}} \)
\( \mathrm{EA_1(O) = -141\ kJ\,mol^{-1}} \)
\( \mathrm{EA_2(O) = +798\ kJ\,mol^{-1}} \)
Calculate the lattice energy of magnesium oxide.
▶️ Answer / Explanation
Applying Hess’s Law:
\( \mathrm{\Delta H_{latt} = \Delta H_f^\circ – [\Delta H_{at}(Mg) + IE_1 + IE_2 + \Delta H_{at}(O) + EA_1 + EA_2]} \)
\( \mathrm{\Delta H_{latt} = -602 – [150 + 738 + 1451 + 249 – 141 + 798]} \)
\( \mathrm{\Delta H_{latt} = -602 – 3245} \)
\( \mathrm{\Delta H_{latt} = -3847\ kJ\,mol^{-1}} \)
Factors Affecting Lattice Energy
The lattice energy of an ionic solid depends on the strength of electrostatic attraction between oppositely charged ions. This attraction can be explained qualitatively using ionic charge and ionic radius.
Effect of Ionic Charge
As the charge on the ions increases, the lattice energy becomes more exothermic.
Higher charges lead to stronger electrostatic attraction between ions.
For example, compounds containing \( \mathrm{2+} \) and \( \mathrm{2-} \) ions have larger (more negative) lattice energies than those containing \( \mathrm{1+} \) and \( \mathrm{1-} \) ions.
Effect of Ionic Radius
As the ionic radius decreases, the lattice energy becomes more exothermic.

Smaller ions allow oppositely charged ions to be closer together, increasing the electrostatic attraction.
Larger ions have their charges spread over a greater volume, leading to weaker attractions and a less exothermic lattice energy.
Example
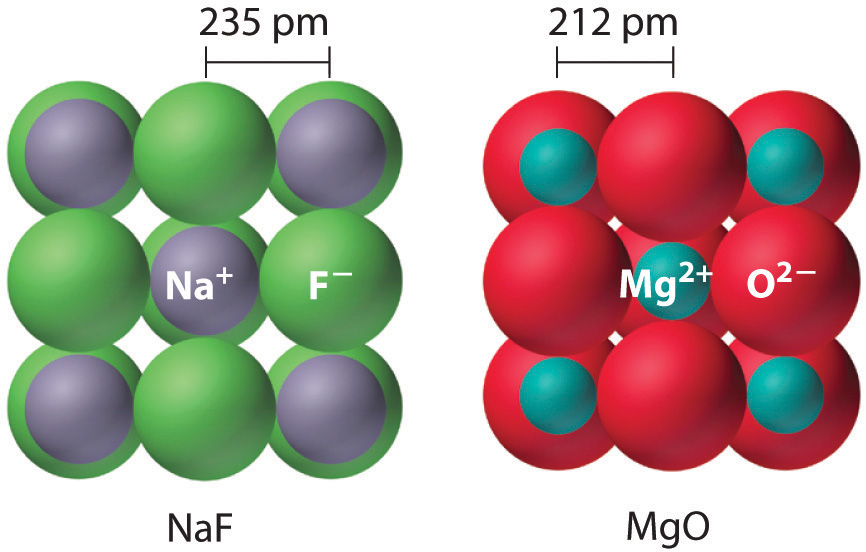
Explain why the lattice energy of magnesium oxide is more exothermic than that of sodium chloride.
▶️ Answer / Explanation
Magnesium oxide contains \( \mathrm{Mg^{2+}} \) and \( \mathrm{O^{2-}} \) ions.
Sodium chloride contains \( \mathrm{Na^+} \) and \( \mathrm{Cl^-} \) ions.
The higher ionic charges in magnesium oxide cause stronger electrostatic attraction.
This leads to a more exothermic lattice energy.
Example
Explain why the lattice energy of lithium fluoride is more exothermic than that of sodium iodide.
▶️ Answer / Explanation
Lithium fluoride contains smaller ions than sodium iodide.
Smaller ionic radii allow ions to be closer together.
This increases the electrostatic attraction between oppositely charged ions.
As a result, lithium fluoride has a more exothermic lattice energy.