CIE AS/A Level Chemistry 23.2 Enthalpies of solution and hydration Study Notes- 2025-2027 Syllabus
CIE AS/A Level Chemistry 23.2 Enthalpies of solution and hydration Study Notes – New Syllabus
CIE AS/A Level Chemistry 23.2 Enthalpies of solution and hydration Study Notes at IITian Academy focus on specific topic and type of questions asked in actual exam. Study Notes focus on AS/A Level Chemistry latest syllabus with Candidates should be able to:
define and use the term enthalpy change with reference to hydration, ΔHₕᵧ𝒹, and solution, ΔHₛₒₗ
construct and use an energy cycle involving enthalpy change of solution, lattice energy and enthalpy change of hydration
carry out calculations involving the energy cycles in 23.2.2
explain, in qualitative terms, the effect of ionic charge and of ionic radius on the numerical magnitude of an enthalpy change of hydration
Enthalpy Changes: Hydration and Solution
When ionic compounds dissolve in water, energy changes occur due to interactions between ions and water molecules. These are described using the enthalpy changes of hydration and solution.
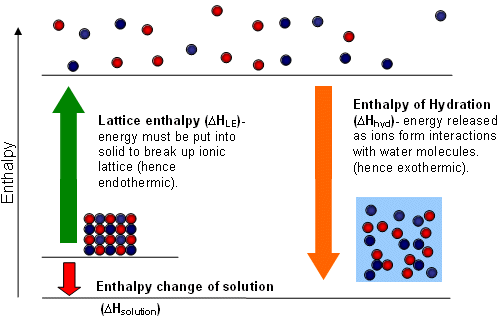
Enthalpy Change of Hydration, \( \mathrm{\Delta H_{hyd}} \)
The enthalpy change of hydration is defined as the enthalpy change when one mole of gaseous ions becomes surrounded by water molecules to form one mole of aqueous ions.
This enthalpy change is always exothermic.
Example equation: \( \mathrm{Na^+(g) \rightarrow Na^+(aq)} \)
Enthalpy Change of Solution, \( \mathrm{\Delta H_{sol}} \)
The enthalpy change of solution is defined as the enthalpy change when one mole of an ionic solid dissolves completely in water to form aqueous ions.
Example equation: \( \mathrm{NaCl(s) \rightarrow Na^+(aq) + Cl^-(aq)} \)
The enthalpy change of solution depends on the balance between lattice energy and enthalpy changes of hydration.
Relationship:
\( \mathrm{\Delta H_{sol} = \Delta H_{latt} + \sum \Delta H_{hyd}} \)
Example
Write an equation to represent the enthalpy change of hydration of a chloride ion.
▶️ Answer / Explanation
The chloride ion must be in the gaseous state before hydration.
The correct equation is:
\( \mathrm{Cl^-(g) \rightarrow Cl^-(aq)} \)
Example
Explain why the enthalpy change of solution of magnesium chloride is more exothermic than that of sodium chloride.
▶️ Answer / Explanation
Magnesium chloride produces ions with higher charge.
The \( \mathrm{Mg^{2+}} \) ion has a higher charge density than \( \mathrm{Na^+} \).
This results in more exothermic enthalpy changes of hydration.
The greater hydration energy outweighs the lattice energy, making dissolution more exothermic.
Energy Cycles Involving Enthalpy of Solution
When an ionic solid dissolves in water, the overall energy change can be analysed using an energy cycle involving lattice energy and enthalpy changes of hydration. This cycle is based on Hess’s Law.
Steps in the Energy Cycle
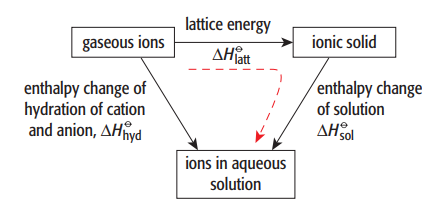
- Separate the ionic solid into gaseous ions (lattice energy)
- Hydrate the gaseous ions to form aqueous ions
- Combine these steps to give the enthalpy change of solution
Key Enthalpy Changes
Lattice energy, \( \mathrm{\Delta H_{latt}} \): enthalpy change when one mole of an ionic solid is formed from its gaseous ions.
Enthalpy change of hydration, \( \mathrm{\Delta H_{hyd}} \): enthalpy change when one mole of gaseous ions forms aqueous ions.
Enthalpy change of solution, \( \mathrm{\Delta H_{sol}} \): enthalpy change when one mole of an ionic solid dissolves in water.
Energy Cycle Relationship
The enthalpy change of solution is given by:
\( \mathrm{\Delta H_{sol} = -\Delta H_{latt} + \sum \Delta H_{hyd}} \)
The sign of \( \mathrm{\Delta H_{sol}} \) depends on the balance between the energy required to separate ions and the energy released when ions are hydrated.
Example
Explain, using an energy cycle, why the enthalpy change of solution of sodium chloride is close to zero.
▶️ Answer / Explanation
Energy is required to overcome the lattice energy of sodium chloride.
Energy is released when the sodium and chloride ions are hydrated.
The lattice energy and hydration enthalpies are similar in magnitude.
This results in an enthalpy change of solution close to zero.
Example
The following data are given for potassium bromide:
\( \mathrm{\Delta H_{latt}(KBr) = -671\ kJ\,mol^{-1}} \)
\( \mathrm{\Delta H_{hyd}(K^+) = -322\ kJ\,mol^{-1}} \)
\( \mathrm{\Delta H_{hyd}(Br^-) = -347\ kJ\,mol^{-1}} \)
Calculate the enthalpy change of solution of potassium bromide.
▶️ Answer / Explanation
\( \mathrm{\Delta H_{sol} = -(-671) + (-322 + -347)} \)
\( \mathrm{\Delta H_{sol} = 671 – 669} \)
\( \mathrm{\Delta H_{sol} = +2\ kJ\,mol^{-1}} \)
The dissolution is approximately thermally neutral.
Calculations Using Energy Cycles
Energy cycles are used to calculate enthalpy changes that cannot be measured directly. These calculations are based on Hess’s Law, which states that the total enthalpy change for a reaction is independent of the route taken.
General Method for Energy Cycle Calculations
- Write down all relevant enthalpy changes involved
- Decide which enthalpy change is required
- Write an equation linking the enthalpy changes using Hess’s Law
- Substitute values carefully, paying attention to signs
- Calculate the final value with correct units
Common relationships:
For solution cycles:

\( \mathrm{\Delta H_{sol} = -\Delta H_{latt} + \sum \Delta H_{hyd}} \)
For Born–Haber cycles:

\( \mathrm{\Delta H_{latt} = \Delta H_f^\circ – \text{(sum of other steps)}} \)
Example
The following data are given for sodium fluoride:
\( \mathrm{\Delta H_{latt} = -923\ kJ\,mol^{-1}} \)
\( \mathrm{\Delta H_{hyd}(Na^+) = -406\ kJ\,mol^{-1}} \)
\( \mathrm{\Delta H_{hyd}(F^-) = -506\ kJ\,mol^{-1}} \)
Calculate the enthalpy change of solution of sodium fluoride.
▶️ Answer / Explanation
Use the equation:
\( \mathrm{\Delta H_{sol} = -\Delta H_{latt} + \sum \Delta H_{hyd}} \)
Substitute the values:
\( \mathrm{\Delta H_{sol} = -(-923) + (-406 + -506)} \)
\( \mathrm{\Delta H_{sol} = 923 – 912} \)
\( \mathrm{\Delta H_{sol} = +11\ kJ\,mol^{-1}} \)
Example
The following data are given for calcium chloride:
\( \mathrm{\Delta H_f^\circ(CaCl_2) = -795\ kJ\,mol^{-1}} \)
\( \mathrm{\Delta H_{at}(Ca) = +178\ kJ\,mol^{-1}} \)
\( \mathrm{IE_1(Ca) = +590\ kJ\,mol^{-1}} \)
\( \mathrm{IE_2(Ca) = +1145\ kJ\,mol^{-1}} \)
\( \mathrm{\Delta H_{at}(Cl) = +121\ kJ\,mol^{-1}} \)
\( \mathrm{EA_1(Cl) = -349\ kJ\,mol^{-1}} \)
Calculate the lattice energy of calcium chloride.
▶️ Answer / Explanation
Two chlorine atoms are involved.
Apply Hess’s Law:
\( \mathrm{\Delta H_{latt} = \Delta H_f^\circ – [\Delta H_{at}(Ca) + IE_1 + IE_2 + 2(\Delta H_{at}(Cl)) + 2(EA_1)]} \)
\( \mathrm{\Delta H_{latt} = -795 – [178 + 590 + 1145 + 2(121) + 2(-349)]} \)
\( \mathrm{\Delta H_{latt} = -795 – 1457} \)
\( \mathrm{\Delta H_{latt} = -2252\ kJ\,mol^{-1}} \)
Factors Affecting Enthalpy Change of Hydration
The enthalpy change of hydration depends on the strength of attraction between an ion and surrounding water molecules. This attraction is described in terms of charge density.
Effect of Ionic Charge
As the charge on an ion increases, the enthalpy change of hydration becomes more exothermic.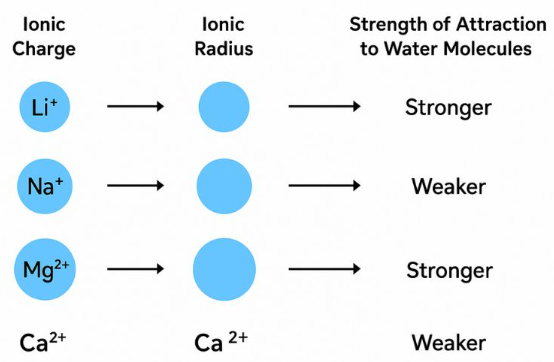
Ions with higher charge form stronger ion–dipole attractions with water molecules.
For example, \( \mathrm{Mg^{2+}} \) releases more energy on hydration than \( \mathrm{Na^+} \).
Effect of Ionic Radius
As the ionic radius decreases, the enthalpy change of hydration becomes more exothermic.
Smaller ions have a higher charge density, leading to stronger attraction to water molecules.
Larger ions have lower charge density and therefore weaker hydration.
Overall, ions with high charge and small radius have the most exothermic enthalpy changes of hydration.
Example
Explain why the enthalpy change of hydration of \( \mathrm{Al^{3+}} \) is more exothermic than that of \( \mathrm{Na^+} \).
▶️ Answer / Explanation
\( \mathrm{Al^{3+}} \) has a higher ionic charge than \( \mathrm{Na^+} \).
It also has a smaller ionic radius.
This gives \( \mathrm{Al^{3+}} \) a higher charge density.
Stronger ion–dipole attractions release more energy on hydration.
Example
Explain why the enthalpy change of hydration of \( \mathrm{Li^+} \) is more exothermic than that of \( \mathrm{K^+} \).
▶️ Answer / Explanation
Both ions have the same charge.
\( \mathrm{Li^+} \) has a much smaller ionic radius than \( \mathrm{K^+} \).
This results in a higher charge density for \( \mathrm{Li^+} \).
Stronger ion–dipole attractions lead to a more exothermic hydration enthalpy.
