CIE AS/A Level Chemistry 5.1 Enthalpy change, $\Delta H$ Study Notes- 2025-2027 Syllabus
CIE AS/A Level Chemistry 5.1 Enthalpy change, $\Delta H$ Study Notes – New Syllabus
CIE AS/A Level Chemistry 5.1 Enthalpy change, $\Delta H$ Study Notes at IITian Academy focus on specific topic and type of questions asked in actual exam. Study Notes focus on AS/A Level Chemistry latest syllabus with Candidates should be able to:
Enthalpy Changes in Chemical Reactions — Exothermic and Endothermic
Chemical reactions are accompanied by energy changes. The heat energy exchanged with the surroundings at constant pressure is called the enthalpy change, represented by \( \Delta H \).
Definition of Enthalpy Change
Enthalpy change \( \Delta H \) is the heat energy transferred during a chemical reaction at constant pressure.
Exothermic Reactions
- Release heat energy to the surroundings.
- The surroundings get hotter.
- \( \Delta H \) is negative.
- Products have lower enthalpy than reactants.
Example: combustion \( \mathrm{CH_4 + 2O_2 \rightarrow CO_2 + 2H_2O} \) \( \Delta H < 0 \)
Endothermic Reactions
- Absorb heat energy from the surroundings.
- The surroundings get colder.
- \( \Delta H \) is positive.
- Products have higher enthalpy than reactants.
Example: thermal decomposition \( \mathrm{CaCO_3 \rightarrow CaO + CO_2} \) \( \Delta H > 0 \)
Energy Level Diagrams
- Exothermic → energy released → downward enthalpy profile.
- Endothermic → energy absorbed → upward enthalpy profile.
Direction of \( \Delta H \):
- Exothermic: \( \Delta H < 0 \)
- Endothermic: \( \Delta H > 0 \)
Example
State whether the following reaction is exothermic or endothermic: \( \mathrm{N_2 + 3H_2 \rightarrow 2NH_3} \) with \( \Delta H = -92\ \mathrm{kJ\ mol^{-1}} \).
▶️ Answer / Explanation
\( \Delta H \) is negative → the reaction releases heat → exothermic.
Example
Explain why an endothermic reaction causes the temperature of the surroundings to fall.
▶️ Answer / Explanation
An endothermic reaction absorbs heat energy from the surroundings. As the surroundings lose heat, their temperature decreases.
Example
A reaction has \( \Delta H = +178\ \mathrm{kJ\ mol^{-1}} \). Describe the relative enthalpy of reactants and products and explain why heat must be supplied.
▶️ Answer / Explanation
\( \Delta H > 0 \) → products have higher enthalpy than reactants.
The system must absorb energy to reach the higher enthalpy level of the products.
Therefore heat must be supplied → endothermic process.
Reaction Pathway Diagrams — Enthalpy Change and Activation Energy
A reaction pathway diagram (also called an energy profile diagram) shows how the energy of the system changes during the course of a chemical reaction. It illustrates:
- The enthalpy of reactants and products
- The enthalpy change \( \Delta H \)
- The activation energy \( E_a \)
- The difference between exothermic and endothermic pathways
Enthalpy Change \( \Delta H \)
The enthalpy change is the difference in enthalpy between products and reactants:
\( \Delta H = H_{\text{products}} – H_{\text{reactants}} \)
- Exothermic: \( \Delta H < 0 \), products lower in energy
- Endothermic: \( \Delta H > 0 \), products higher in energy
Activation Energy \( E_a \)
Activation energy is the minimum energy required to start a reaction. It corresponds to the energy needed to reach the transition state.
\( E_a = H_{\text{transition state}} – H_{\text{reactants}} \)
Reaction Pathway Diagrams
- Exothermic profile: energy decreases as products form; \( \Delta H \) negative.
- Endothermic profile: energy increases; \( \Delta H \) positive.
- The peak always represents the transition state (highest energy point).
- The energy gap between reactants and the peak is the activation energy.
Although diagrams cannot be drawn here, the key interpretation is:
• Reactants → Peak (activation energy) → Products
• Drop or rise in final enthalpy shows whether the reaction is exothermic or endothermic
Example
In a reaction pathway diagram, the products are lower in energy than the reactants. What type of reaction is shown?
▶️ Answer / Explanation
Products lower in energy → \( \Delta H < 0 \) → Exothermic reaction.
Example
The activation energy is shown as a large vertical arrow. Explain what this indicates about the reaction rate.
▶️ Answer / Explanation
A large activation energy means particles need a lot of energy to react. Therefore, the reaction is slow at room temperature because few particles can overcome the energy barrier.
Example
A reaction has \( H_{\text{reactants}} = 120\ \mathrm{kJ\ mol^{-1}} \), \( H_{\text{products}} = 200\ \mathrm{kJ\ mol^{-1}} \), and the transition state at \( 310\ \mathrm{kJ\ mol^{-1}} \). Calculate \( \Delta H \) and \( E_a \).
▶️ Answer / Explanation
\( \Delta H = H_{\text{products}} – H_{\text{reactants}} = 200 – 120 = +80\ \mathrm{kJ\ mol^{-1}} \) (endothermic)
\( E_a = H_{\text{transition state}} – H_{\text{reactants}} = 310 – 120 = 190\ \mathrm{kJ\ mol^{-1}} \)
The reaction absorbs energy and has a high activation energy → slow without heating or a catalyst.
Standard Conditions and Types of Enthalpy Change
Enthalpy changes are often measured under standard conditions, represented by the superscript ⦵ (standard enthalpies). Different types of enthalpy change describe different chemical processes.
(a) Standard Conditions (⦵)
Standard conditions (shown by the symbol ⦵) are:
- Temperature: \( 298\ \mathrm{K} \)
- Pressure: \( 101\ \mathrm{kPa} \)
- All substances in their standard physical states
Standard enthalpy changes are written as \( \Delta H^\circ \).
(b) Types of Enthalpy Changes
1. Standard Enthalpy Change of Reaction, \( \Delta H_\mathrm{r}^\circ \)
The enthalpy change when a reaction occurs in the molar quantities shown in a chemical equation under standard conditions.
2. Standard Enthalpy Change of Formation, \( \Delta H_\mathrm{f}^\circ \)
The enthalpy change when 1 mole of a compound is formed from its elements in their standard states under standard conditions.
Example formation equation: \( \mathrm{C(s) + O_2(g) \rightarrow CO_2(g)} \)
3. Standard Enthalpy Change of Combustion, \( \Delta H_\mathrm{c}^\circ \)
The enthalpy change when 1 mole of a substance is completely burned in oxygen under standard conditions.
Example: \( \mathrm{CH_4(g) + 2O_2(g) \rightarrow CO_2(g) + 2H_2O(l)} \)
4. Standard Enthalpy Change of Neutralisation, \( \Delta H_\mathrm{neut}^\circ \)
The enthalpy change when an acid and a base react to form 1 mole of water under standard conditions.
General reaction: \( \mathrm{H^+(aq) + OH^-(aq) \rightarrow H_2O(l)} \)
Example
State the temperature and pressure used in standard conditions (⦵).
▶️ Answer / Explanation
Standard conditions are \( 298\ \mathrm{K} \) and \( 101\ \mathrm{kPa} \).
Example
Write the equation for the standard enthalpy change of formation of \( \mathrm{NH_3(g)} \).
▶️ Answer / Explanation
The formation of 1 mole of \( \mathrm{NH_3(g)} \):
\( \mathrm{\frac{1}{2}N_2(g) + \frac{3}{2}H_2(g) \rightarrow NH_3(g)} \)
Elements must be in their standard states.
Example
Explain why the standard enthalpy change of neutralisation is almost always around \( -57\ \mathrm{kJ\ mol^{-1}} \) for reactions involving strong acids and strong bases.
▶️ Answer / Explanation
Strong acids and bases fully dissociate, so the reaction is always:
\( \mathrm{H^+(aq) + OH^-(aq) \rightarrow H_2O(l)} \)
The same ions react each time → same enthalpy change.
The formation of water from \( \mathrm{H^+} \) and \( \mathrm{OH^-} \) always releases about \( -57\ \mathrm{kJ\ mol^{-1}} \).
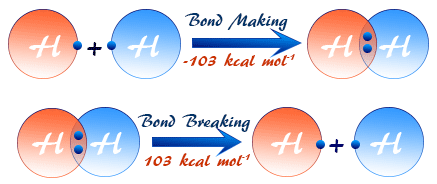
Energy Transfers in Chemical Reactions — Breaking and Making Bonds
Chemical reactions involve the breaking of bonds in reactants and the forming of new bonds in products. These two processes require and release different amounts of energy, leading to overall enthalpy changes.
Bond Breaking (Endothermic Process)
- Energy must be supplied to break chemical bonds.
- Bond breaking absorbs heat → endothermic.
- \( \Delta H > 0 \) for bond breaking.
Example: Breaking \( \mathrm{H_2} \) into atoms requires energy.
Bond Making (Exothermic Process)
- Energy is released when new bonds form.
- Bond formation gives out heat → exothermic.
- \( \Delta H < 0 \) for bond making.
Example: Forming \( \mathrm{H-O} \) bonds in water releases energy.
Overall Enthalpy Change of a Reaction
The overall enthalpy change depends on the balance between energy absorbed during bond breaking and energy released during bond formation:
\( \Delta H = \text{Energy absorbed (breaking)} – \text{Energy released (forming)} \)
- Exothermic reaction → more energy released from bond formation than absorbed in bond breaking.
- Endothermic reaction → more energy absorbed to break bonds than released when new bonds form.
Example
Is bond breaking exothermic or endothermic?
▶️ Answer / Explanation
Bond breaking is endothermic because energy must be absorbed to separate atoms.
Example
Explain why forming bonds releases energy.
▶️ Answer / Explanation
Bond formation creates a more stable, lower-energy arrangement of atoms. The excess energy is released to the surroundings as the system moves to a lower energy state.
Example
A reaction absorbs \( 350\ \mathrm{kJ\ mol^{-1}} \) to break bonds but releases \( 500\ \mathrm{kJ\ mol^{-1}} \) when new bonds form. Determine whether the reaction is exothermic or endothermic, and calculate \( \Delta H \).
▶️ Answer / Explanation
\( \Delta H = 350 – 500 = -150\ \mathrm{kJ\ mol^{-1}} \)
Because \( \Delta H \) is negative, the reaction is exothermic.
Using Bond Energies to Calculate Enthalpy Change of Reaction, \( \Delta H_\mathrm{r} \)
Bond energies represent the energy required to break one mole of a covalent bond in the gaseous state. All bond energies are positive because breaking bonds is endothermic.
Key Idea
To calculate the enthalpy change of a reaction using bond energies:
\( \Delta H_\mathrm{r} = \text{Energy absorbed in breaking bonds} – \text{Energy released in forming bonds} \)
- Breaking bonds → endothermic → energy absorbed → positive values.
- Forming bonds → exothermic → energy released → negative contribution.
Steps for Calculation
- Write out the balanced chemical equation.
- Identify all bonds broken (reactants) and bonds formed (products).
- Multiply each bond by its bond energy.
- Apply the formula:
\( \Delta H_\mathrm{r} = \Sigma E_\text{broken} – \Sigma E_\text{formed} \)
Example
Breaking a single \( \mathrm{H-H} \) bond requires \( 436\ \mathrm{kJ\ mol^{-1}} \). What is the energy change for breaking 1 mole of \( \mathrm{H-H} \) bonds?
▶️ Answer / Explanation
Bond breaking is endothermic. Energy absorbed = \( +436\ \mathrm{kJ\ mol^{-1}} \).
Example
Use the following bond energies to calculate \( \Delta H_\mathrm{r} \) for: \( \mathrm{H_2 + Cl_2 \rightarrow 2HCl} \)
\( \mathrm{H-H = 436\ kJ\ mol^{-1}} \) \( \mathrm{Cl-Cl = 243\ kJ\ mol^{-1}} \) \( \mathrm{H-Cl = 431\ kJ\ mol^{-1}} \)
▶️ Answer / Explanation
Bonds broken:
\( 1 \times \mathrm{H-H} = 436 \)
\( 1 \times \mathrm{Cl-Cl} = 243 \)
Total broken = \( 436 + 243 = 679\ \mathrm{kJ\ mol^{-1}} \)
Bonds formed:
\( 2 \times \mathrm{H-Cl} = 2 \times 431 = 862\ \mathrm{kJ\ mol^{-1}} \)
Overall:
\( \Delta H_\mathrm{r} = 679 – 862 = -183\ \mathrm{kJ\ mol^{-1}} \)
Reaction is exothermic.
Example
Calculate \( \Delta H_\mathrm{r} \) for the reaction: \( \mathrm{CH_4 + 2O_2 \rightarrow CO_2 + 2H_2O} \)
Bond energies (in \( \mathrm{kJ\ mol^{-1}} \)): \( \mathrm{C-H = 412} \), \( \mathrm{O=O = 498} \), \( \mathrm{C=O = 805} \), \( \mathrm{O-H = 463} \)
▶️ Answer / Explanation
Bonds broken (reactants):
\( 4 \times \mathrm{C-H} = 4 \times 412 = 1648 \)
\( 2 \times \mathrm{O=O} = 2 \times 498 = 996 \)
Total broken = \( 1648 + 996 = 2644\ \mathrm{kJ\ mol^{-1}} \)
Bonds formed (products):
\( 2 \times \mathrm{C=O} = 2 \times 805 = 1610 \)
\( 4 \times \mathrm{O-H} = 4 \times 463 = 1852 \)
Total formed = \( 1610 + 1852 = 3462\ \mathrm{kJ\ mol^{-1}} \)
Overall enthalpy change:
\( \Delta H_\mathrm{r} = 2644 – 3462 = -818\ \mathrm{kJ\ mol^{-1}} \)
The reaction is highly exothermic.
Exact and Average Bond Energies
Bond energies represent the energy required to break one mole of a specific covalent bond in the gaseous state. However, the value of a bond energy can vary depending on the chemical environment of the bond. Therefore, some bond energies are exact while others are average values.
Exact Bond Energies
- Found in diatomic molecules where the environment of each bond is identical.
- Example: \( \mathrm{H-H} \), \( \mathrm{Cl-Cl} \), \( \mathrm{Br-Br} \), \( \mathrm{F-F} \)
- The bond energy measured is exact because there is only one type of bond present.
Example: Bond energy of \( \mathrm{H-H} \) is an exact value.
Average Bond Energies
- Used for bonds in polyatomic molecules where the same type of bond occurs in different environments.
- The energy needed to break a C–H bond, for example, differs slightly between methane, ethane, ethanol, etc.
- Average bond energies are therefore calculated by averaging many experimental values.
- Used when calculating enthalpy changes from bond energies.
Example: The C–H bond has slightly different strengths in \( \mathrm{CH_4} \), \( \mathrm{C_2H_6} \), \( \mathrm{C_2H_4} \), so we use an average.
Why Average Bond Energies Are Needed
- In real molecules, bond strength depends on: – surrounding atoms – molecular shape – hybridisation – polarity
- It is often impossible to measure a single bond energy in isolation.
- Averages allow us to perform approximate calculations of \( \Delta H_\mathrm{r} \).
Example
Is the bond energy of the \( \mathrm{H-H} \) bond exact or average?
▶️ Answer / Explanation
Exact — because \( \mathrm{H_2} \) contains only one type of bond in a single environment.
Example
Explain why the C–H bond energy is not an exact value.
▶️ Answer / Explanation
The strength of a C–H bond changes depending on the molecule (e.g., methane vs. ethane vs. benzene). The chemical environment affects the bond strength, so an average value must be used.
Example
A student calculates \( \Delta H_\mathrm{r} \) using average bond energies and obtains a value significantly different from the experimental enthalpy change. Explain why.
▶️ Answer / Explanation
Average bond energies are approximations derived from multiple molecules. In a specific reaction, the real bond energies may differ from the averaged values due to differences in structure, polarity, or molecular environment. Therefore the calculated \( \Delta H_\mathrm{r} \) is approximate, not exact.
Calculating Enthalpy Changes from Experimental Results
Experimental enthalpy changes can be calculated using temperature changes measured during a reaction. The heat energy transferred to or from a substance can be found using the equation:
\( q = mc\Delta T \)
The Formula \( q = mc\Delta T \)
- \( q \) = heat energy transferred (in \( \mathrm{J} \))
- \( m \) = mass of solution/water heated (in \( \mathrm{g} \))
- \( c \) = specific heat capacity \( \mathrm{4.18\ J\ g^{-1}\ K^{-1}} \) (for water/aqueous solutions)
- \( \Delta T \) = temperature change (in \( \mathrm{K} \) or \( ^\circ\mathrm{C} \))
If the reaction occurs in solution, the mass used is the mass of the solution (1 \( \mathrm{cm^3} \) ≈ 1 g).
Calculating Enthalpy Change per Mole
Once the heat energy \( q \) is calculated, the enthalpy change per mole is:
\( \Delta H = -\dfrac{q}{n} \)
- The negative sign is used because: — temperature rise → exothermic → \( \Delta H < 0 \) — temperature fall → endothermic → \( \Delta H > 0 \)
- \( n \) = moles of the substance reacting (usually limiting reagent)
Important Notes
- Convert \( q \) from J to kJ by dividing by 1000 when giving \( \Delta H \) in \( \mathrm{kJ\ mol^{-1}} \).
- Use correct number of significant figures based on the data.
- Assume the solution has the same specific heat capacity as water unless told otherwise.
Example
50 g of water is heated from 20°C to 30°C. Calculate the heat absorbed.
▶️ Answer / Explanation
\( m = 50\ \mathrm{g} \), \( c = 4.18 \), \( \Delta T = 10 \)
\( q = mc\Delta T = 50 \times 4.18 \times 10 = 2090\ \mathrm{J} \)
Example
A student dissolves 1.50 g of NaOH in 100 g of water. The temperature increases by 6.0°C. Calculate \( \Delta H_\mathrm{neut} \).
▶️ Answer / Explanation
Step 1: Calculate heat released
\( m = 100\ \mathrm{g},\ \Delta T = 6.0,\ c = 4.18 \)
\( q = 100 \times 4.18 \times 6.0 = 2508\ \mathrm{J} \)
Step 2: Find moles of NaOH
Molar mass of NaOH = 40 g mol\(^{-1}\)
\( n = \dfrac{1.50}{40} = 0.0375\ \mathrm{mol} \)
Step 3: Calculate \( \Delta H \)
\( \Delta H = -\dfrac{q}{n} = -\dfrac{2508}{0.0375} = -66900\ \mathrm{J\ mol^{-1}} \)
= \( -66.9\ \mathrm{kJ\ mol^{-1}} \)
This matches typical neutralisation values (≈ -57 to -70).
Example
When 25.0 cm³ of \( 2.00\ \mathrm{mol\ dm^{-3}} \) HCl reacts with excess Mg, the temperature rises from 22.5°C to 37.0°C. Calculate the enthalpy change of reaction per mole of HCl.
▶️ Answer / Explanation
Step 1: Calculate heat released
Total solution mass ≈ 25 g (25 cm³)
\( \Delta T = 37.0 – 22.5 = 14.5^\circ\mathrm{C} \)
\( q = mc\Delta T = 25 \times 4.18 \times 14.5 = 1515\ \mathrm{J} \)
Step 2: Moles of HCl
\( n = C \times V = 2.00 \times 0.025 = 0.050\ \mathrm{mol} \)
Step 3: Calculate \( \Delta H \)
\( \Delta H = -\dfrac{1515}{0.050} = -30300\ \mathrm{J\ mol^{-1}} \)
= \( -30.3\ \mathrm{kJ\ mol^{-1}} \)
The reaction is exothermic.