CIE AS/A Level Chemistry 6.1 Redox processes Study Notes- 2025-2027 Syllabus
CIE AS/A Level Chemistry 6.1 Redox processes Study Notes – New Syllabus
CIE AS/A Level Chemistry 6.1 Redox processes Study Notes at IITian Academy focus on specific topic and type of questions asked in actual exam. Study Notes focus on AS/A Level Chemistry latest syllabus with Candidates should be able to:
Calculating Oxidation Numbers
Oxidation numbers (oxidation states) show how many electrons an atom has gained, lost or shared when forming a compound or ion. They are used to keep track of electron transfer in redox reactions.
Rules for Assigning Oxidation Numbers
- The oxidation number of an element in its pure elemental form is \( 0 \).
- Examples:
- \( \mathrm{O_2} \), \( \mathrm{N_2} \), \( \mathrm{Na} \), \( \mathrm{Cl_2} \)
- For a simple ion, oxidation number = ionic charge.
- Examples:
- \( \mathrm{Na^+} = +1 \), \( \mathrm{O^{2-}} = -2 \)
- In compounds, some atoms have fixed oxidation numbers:
- Group 1 metals: \( +1 \)
- Group 2 metals: \( +2 \)
- Aluminium: \( +3 \)
- Oxygen is usually \( -2 \), except in:
- peroxides (e.g., \( \mathrm{H_2O_2} \)): \( -1 \)
- \( \mathrm{OF_2} \): \( +2 \)
- Hydrogen is usually \( +1 \), except in metal hydrides (e.g., \( \mathrm{NaH} \)): \( -1 \)
- Fluorine is always \( -1 \). Other halogens are usually negative except when bonded to oxygen.
- The sum of oxidation numbers in a neutral compound is \( 0 \).
- The sum of oxidation numbers in a polyatomic ion = ion charge.
Method
- Assign known oxidation numbers using standard rules.
- Let the unknown oxidation number be \( x \).
- Set up an equation based on the total charge.
- Solve for \( x \).
Example
Find the oxidation number of chlorine in \( \mathrm{NaCl} \).
▶️ Answer / Explanation
\( \mathrm{Na} = +1 \).
Total must be 0, so Cl = \( -1 \).
Example
Find the oxidation number of sulfur in \( \mathrm{SO_4^{2-}} \).
▶️ Answer / Explanation
Let sulfur = \( x \).
Oxygen = \( -2 \), and there are 4 oxygens → total \( -8 \).
Sum must equal the ion charge \( -2 \):
\( x + (-8) = -2 \)
\( x = +6 \).
Example
Find the oxidation number of nitrogen in \( \mathrm{NH_4^+} \) and in \( \mathrm{NO_3^-} \).
▶️ Answer / Explanation
1. \( \mathrm{NH_4^+} \)
Let N = \( x \).
Hydrogen = \( +1 \), 4 H = \( +4 \).
\( x + 4 = +1 \)
\( x = -3 \).
2. \( \mathrm{NO_3^-} \)
Let N = \( x \).
Oxygen = \( -2 \), 3 O = \( -6 \).
\( x – 6 = -1 \)
\( x = +5 \).
Nitrogen shows different oxidation states in different ions.
Using Changes in Oxidation Numbers to Balance Chemical Equations
Oxidation number changes show how many electrons are lost or gained during a redox reaction. This method helps balance equations by ensuring total electrons lost = total electrons gained.
Key Principles
- Oxidation = increase in oxidation number (loss of electrons).
- Reduction = decrease in oxidation number (gain of electrons).
- In a balanced redox reaction, total increase in oxidation number = total decrease in oxidation number.
- Coefficients are adjusted to ensure electron transfer is balanced.
Method (Oxidation Number Change Method)
- Assign oxidation numbers to all relevant atoms.
- Identify the atoms being oxidised and reduced.
- Calculate the change in oxidation number for each atom.
- Use coefficients to balance electron changes.
- Balance the rest of the atoms (e.g., O with \( \mathrm{H_2O} \), H with \( \mathrm{H^+} \) if acidic, or \( \mathrm{OH^-} \) if alkaline).
- Check that charges and atoms are balanced.
Example
Balance the reaction using oxidation numbers:
\( \mathrm{Fe^{2+} \rightarrow Fe^{3+}} \)
▶️ Answer / Explanation
Oxidation number changes:
\( \mathrm{Fe^{2+} \rightarrow Fe^{3+}} \) = oxidation from +2 to +3 (loss of 1 electron).
Electrons lost = 1.
Already balanced → no coefficients needed.
Balanced half-equation:
\( \mathrm{Fe^{2+} \rightarrow Fe^{3+} + e^-} \)
Example
Balance the redox equation:
\( \mathrm{Cu + NO_3^- \rightarrow Cu^{2+} + NO} \)
▶️ Answer / Explanation
Step 1: Oxidation numbers
Cu: 0 → +2 (oxidation, loss of 2 e\(^{-}\))
N in \( \mathrm{NO_3^-} \): +5 → +2 (reduction, gain of 3 e\(^{-}\))
Step 2: Balance electron changes
LCM of 2 and 3 = 6.
Cu must lose 6 electrons → multiply Cu by 3.
N must gain 6 electrons → multiply nitrate by 2.
Step 3: Add coefficients:
\( \mathrm{3Cu + 2NO_3^- \rightarrow 3Cu^{2+} + 2NO} \)
Step 4: Balance O and H (acidic):
Add 6 \( \mathrm{H_2O} \) to the product side and 12 \( \mathrm{H^+} \) to the reactant side.
Final answer:
\( \mathrm{3Cu + 2NO_3^- + 8H^+ \rightarrow 3Cu^{2+} + 2NO + 4H_2O} \)
Example
Balance the following in acidic solution:
\( \mathrm{MnO_4^- + Fe^{2+} \rightarrow Mn^{2+} + Fe^{3+}} \)
▶️ Answer / Explanation
Step 1: Oxidation number changes
\( \mathrm{MnO_4^-} \): Mn = +7 → +2 (gain of 5 e\(^{-}\))
\( \mathrm{Fe^{2+}} \): +2 → +3 (loss of 1 e\(^{-}\))
Step 2: Balance electrons
Fe must lose 5 electrons → multiply Fe\(^{2+}\) by 5.
Step 3: Add coefficients:
\( \mathrm{MnO_4^- + 5Fe^{2+} \rightarrow Mn^{2+} + 5Fe^{3+}} \)
Step 4: Balance O and H (acidic)
MnO\( _4^- \) has 4 O → add 4 \( \mathrm{H_2O} \) to products.
Add 8 \( \mathrm{H^+} \) to reactants.
Final balanced equation:
\( \mathrm{MnO_4^- + 8H^+ + 5Fe^{2+} \rightarrow Mn^{2+} + 4H_2O + 5Fe^{3+}} \)
Redox, Oxidation, Reduction and Disproportionation
Redox reactions involve the transfer of electrons. Oxidation and reduction always occur together because one species loses electrons and another species gains them. These processes can also be described using changes in oxidation number.
Oxidation
- In terms of electrons: loss of electrons → \( \mathrm{Oxidation: \ X \rightarrow X^{n+} + ne^-} \)
- In terms of oxidation number: increase in oxidation number → example: \( \mathrm{Fe^{2+} \rightarrow Fe^{3+}} \)
Reduction
- In terms of electrons: gain of electrons → \( \mathrm{Reduction: \ X^{n+} + ne^- \rightarrow X} \)
- In terms of oxidation number: decrease in oxidation number → example: \( \mathrm{Cl_2 \rightarrow 2Cl^-} \)
Redox
A reaction in which oxidation and reduction occur simultaneously. Electrons lost by one species are gained by another.
Example: \( \mathrm{Zn + Cu^{2+} \rightarrow Zn^{2+} + Cu} \) Zn is oxidised, Cu\(^{2+}\) is reduced.
Disproportionation
A reaction where the same element is oxidised and reduced simultaneously.
- Oxidation number increases in one product and decreases in another.
- Occurs often in compounds of chlorine, nitrogen and transition metals.
Example: \( \mathrm{Cl_2 + 2OH^- \rightarrow Cl^- + ClO^- + H_2O} \)
Here: Cl\( _2 \) (0) → Cl\( ^- \) (−1) : reduction Cl\( _2 \) (0) → ClO\( ^- \) (+1) : oxidation This is a disproportionation reaction.
Example
Identify whether the process is oxidation or reduction:
\( \mathrm{Fe^{3+} + e^- \rightarrow Fe^{2+}} \)
▶️ Answer / Explanation
The species gains an electron → this is reduction.
Oxidation number decreases from +3 to +2.
Example
Determine which species is oxidised and which is reduced in:
\( \mathrm{2Fe^{2+} + Cl_2 \rightarrow 2Fe^{3+} + 2Cl^-} \)
▶️ Answer / Explanation
Iron: \( \mathrm{Fe^{2+} \rightarrow Fe^{3+}} \) Oxidation number increases (+2 → +3) → iron is oxidised.
Chlorine: \( \mathrm{Cl_2 \rightarrow 2Cl^-} \) Oxidation number decreases (0 → -1) → chlorine is reduced.
Example
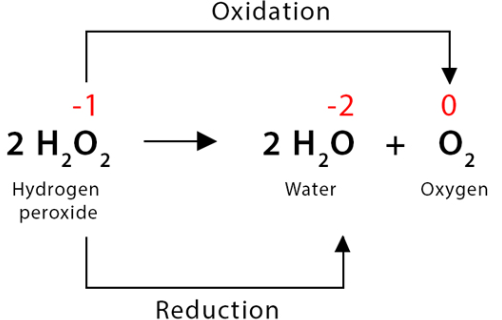
Explain why the reaction below is a disproportionation reaction:
\( \mathrm{2H_2O_2 \rightarrow 2H_2O + O_2} \)
▶️ Answer / Explanation
Oxygen in \( \mathrm{H_2O_2} \) has an oxidation number of −1.
Reduction:
\( \mathrm{O^{-1} \rightarrow O^{2-}} \) in \( \mathrm{H_2O} \)
Oxidation:
\( \mathrm{O^{-1} \rightarrow O^{0}} \) in \( \mathrm{O_2} \)
Same oxygen species is both oxidised and reduced → disproportionation.
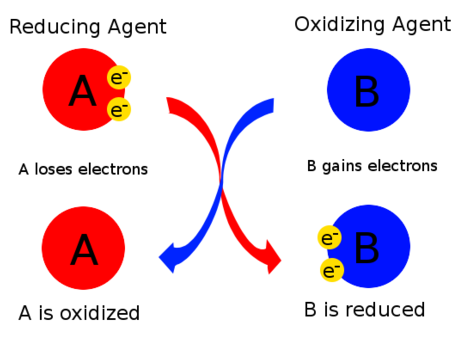
Oxidising Agents and Reducing Agents
Oxidising and reducing agents are substances that bring about oxidation and reduction in other species during a chemical reaction. They can be identified by considering electron transfer and changes in oxidation number.
Oxidising Agent
A species that oxidises another substance.
- It does this by causing that substance to lose electrons.
- Therefore, the oxidising agent itself is reduced.
- Its oxidation number decreases.
Example: \( \mathrm{Cl_2 + 2e^- \rightarrow 2Cl^-} \) Chlorine gains electrons → chlorine is the oxidising agent.
Reducing Agent
A species that reduces another substance.
- It does this by causing that substance to gain electrons.
- Therefore, the reducing agent itself is oxidised.
- Its oxidation number increases.
Example: \( \mathrm{Zn \rightarrow Zn^{2+} + 2e^-} \) Zinc loses electrons → zinc is the reducing agent.
How to Identify Oxidising and Reducing Agents
- Look for electron transfer:
• species gaining electrons → oxidising agent
• species losing electrons → reducing agent - Look for oxidation number changes:
• decreasing oxidation number → oxidising agent
• increasing oxidation number → reducing agent - Common oxidising agents include: \( \mathrm{MnO_4^-} \), \( \mathrm{Cr_2O_7^{2-}} \), \( \mathrm{Cl_2} \), \( \mathrm{H_2O_2} \)
- Common reducing agents include: \( \mathrm{Zn} \), \( \mathrm{Fe^{2+}} \), \( \mathrm{CO} \), \( \mathrm{H^-} \) (hydrides)
Example
Identify the oxidising agent in the reaction:
\( \mathrm{Cu^{2+} + Zn \rightarrow Cu + Zn^{2+}} \)
▶️ Answer / Explanation
\( \mathrm{Cu^{2+}} \) gains electrons (is reduced) → it is the oxidising agent.
Example
Identify the reducing agent:
\( \mathrm{2Fe^{3+} + Sn^{2+} \rightarrow 2Fe^{2+} + Sn^{4+}} \)
▶️ Answer / Explanation
\( \mathrm{Sn^{2+}} \) loses electrons (to become \( \mathrm{Sn^{4+}} \)) → it is oxidised → it is the reducing agent.
Example
In the disproportionation reaction:
\( \mathrm{2H_2O_2 \rightarrow 2H_2O + O_2} \)
Identify the oxidising and reducing agents.
▶️ Answer / Explanation
O in \( \mathrm{H_2O_2} \) has oxidation number −1.
Reduction: \( \mathrm{O^{-1} \rightarrow O^{2-}} \) (in \( \mathrm{H_2O} \)) → O is oxidising agent.
Oxidation: \( \mathrm{O^{-1} \rightarrow O^{0}} \) (in \( \mathrm{O_2} \)) → O is reducing agent.
The same species acts as both.
Using Roman Numerals to Indicate Oxidation Numbers
Roman numerals are used in chemical names to show the oxidation number (oxidation state) of an element that can exist in more than one oxidation state. This is especially important for transition metals and some p-block elements.
Why Roman Numerals Are Used
- Many elements form ions with different oxidation numbers.
- Roman numerals specify which oxidation state is present in a compound.
- They appear in parentheses immediately after the element name.
Example: “iron(III) oxide” contains Fe in the \( +3 \) oxidation state.
How Roman Numerals Work
The Roman numeral shows the oxidation number of the element in the compound:
I = 1, II = 2, III = 3, IV = 4, V = 5, VI = 6
Examples:
- iron(II) = Fe\(^{2+}\)
- iron(III) = Fe\(^{3+}\)
- copper(I) = Cu\(^{+}\)
- copper(II) = Cu\(^{2+}\)
- manganese(VII) = Mn\(^{7+}\) (as in \( \mathrm{MnO_4^-} \))
Rules for Assigning Roman Numerals
- Calculate the oxidation number of the element using standard rules.
- Convert the oxidation number into a Roman numeral.
- Place it in parentheses after the element’s name.
Example: \( \mathrm{FeCl_3} \) → Fe = +3 → iron(III) chloride.
Example
Write the name of \( \mathrm{FeO} \) using a Roman numeral.
▶️ Answer / Explanation
Oxygen = \( -2 \).
To balance, Fe must be \( +2 \).
Name: iron(II) oxide.
Example
Determine the oxidation number of N in \( \mathrm{NO_2^-} \) and write its name using a Roman numeral.
▶️ Answer / Explanation
Let N = \( x \).
Oxygen = \( -2 \), 2 O = \( -4 \).
\( x – 4 = -1 \Rightarrow x = +3 \)
Name: nitrogen(III) oxide (in the nitrite ion).
Example
Name the compound \( \mathrm{MnO_4^-} \) using the Roman numeral system and explain your reasoning.
▶️ Answer / Explanation
Let Mn = \( x \).
Oxygen = \( -2 \), 4 O = \( -8 \).
\( x – 8 = -1 \Rightarrow x = +7 \)
Manganese is in the +7 oxidation state.
Name: manganese(VII) oxide (in the permanganate ion).