CIE AS/A Level Maths-1.5 Trigonometry- Study Notes- New Syllabus - 2026-2027
CIE AS/A Level Maths-1.5 Trigonometry- Study Notes- New Syllabus
Ace AS/A Level Maths Exam with CIE AS/A Level Maths-1.5 Trigonometry- Study Notes
Key Concepts:
- Graphs of Sine, Cosine and Tangent Functions
- Exact Values of Standard Angles
- Inverse Trigonometric Functions and Principal Values
- Fundamental Trigonometric Identities
- Solving Simple Trigonometric Equations in a Specified Interval
Graphs of Sine, Cosine and Tangent Functions
Graphs of Sine, Cosine and Tangent Functions
1. Basic Sine Function \(y = \sin x\)
- Domain: all real numbers.
- Range: \([-1, 1]\).
- Period: \(360^\circ\) or \(2\pi \ \text{radians}\).
- Passes through the origin: \((0,0)\).
2. Basic Cosine Function \(y = \cos x\)
- Domain: all real numbers.
- Range: \([-1, 1]\).
- Period: \(360^\circ\) or \(2\pi \ \text{radians}\).
- Starts at \((0,1)\).
3. Basic Tangent Function \(y = \tan x\)
- Domain: all real numbers except where \(\cos x = 0\) (i.e., \(90^\circ, 270^\circ\) or \(\dfrac{\pi}{2}, \dfrac{3\pi}{2}, \dots\)).
- Range: all real numbers.
- Period: \(180^\circ\) or \(\pi \ \text{radians}\).
- Passes through \((0,0)\).
Transformations of Trigonometric Graphs
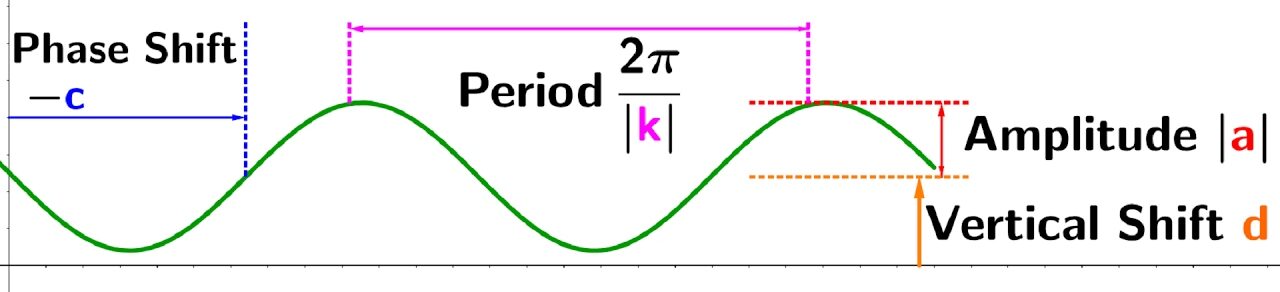
General forms:
- \(y = a \sin x\) or \(y = a \cos x\) → vertical stretch by factor \(|a|\).
- \(y = \sin (bx)\) or \(y = \cos (bx)\) → period changes to \(\dfrac{360^\circ}{b}\) or \(\dfrac{2\pi}{b}\).
- \(y = \sin(x + c)\) or \(y = \cos(x + c)\) → horizontal shift (phase shift) of \(-c\).
- \(y = \sin x + d\) or \(y = \cos x + d\) → vertical shift by \(d\).
Example:
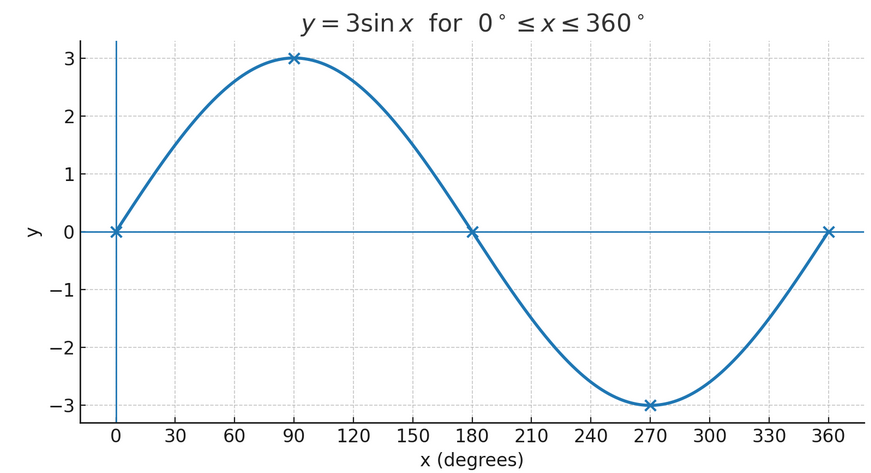
Sketch the graph of \(y = 3 \sin x\) for \(0 \leq x \leq 360^\circ\).
▶️ Answer/Explanation
Step 1: Recall basic sine curve
The basic sine curve oscillates between \(-1\) and \(1\).
Step 2: Apply amplitude change
Since the coefficient is \(3\), the curve will now oscillate between \(-3\) and \(3\).
Step 3: Key points
- \(x = 0^\circ, y = 0\)
- \(x = 90^\circ, y = 3\)
- \(x = 180^\circ, y = 0\)
- \(x = 270^\circ, y = -3\)
- \(x = 360^\circ, y = 0\)
Final Sketch: Standard sine wave but stretched vertically with amplitude \(3\).
Example:
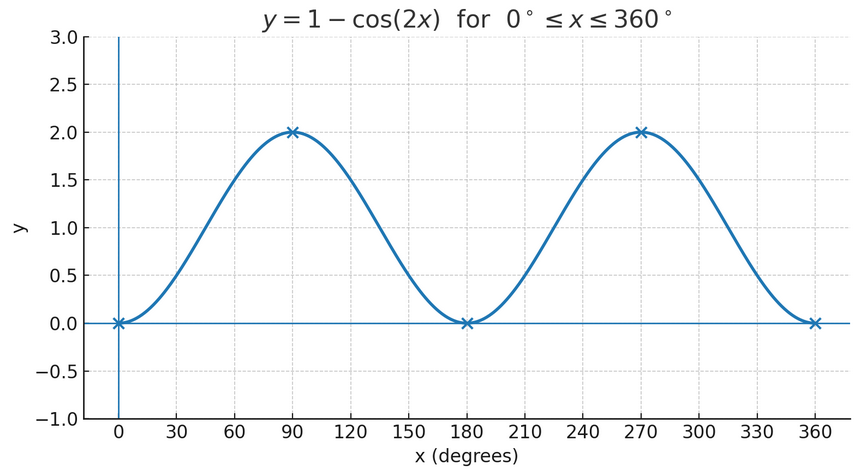
Sketch the graph of \(y = 1 – \cos(2x)\) for \(0 \leq x \leq 360^\circ\).
▶️ Answer/Explanation
Step 1: Recall basic cosine curve
Cosine starts at \(1\), goes down to \(-1\), then returns to \(1\).
Step 2: Apply transformation inside function
Since it is \(\cos(2x)\), the period becomes \(\dfrac{360^\circ}{2} = 180^\circ\).
Step 3: Apply vertical transformation
The graph is shifted because of \(1 – \cos(2x)\): subtracting flips cosine and adds a vertical shift of \(+1\).
Step 4: Key points
- \(x = 0^\circ, y = 0\)
- \(x = 45^\circ, y = 1 – \cos(90^\circ) = 1\)
- \(x = 90^\circ, y = 1 – \cos(180^\circ) = 2\)
- \(x = 180^\circ, y = 0\)
- \(x = 360^\circ, y = 0\)
Final Sketch: A wave oscillating between \(0\) and \(2\), with period \(180^\circ\).
Example:
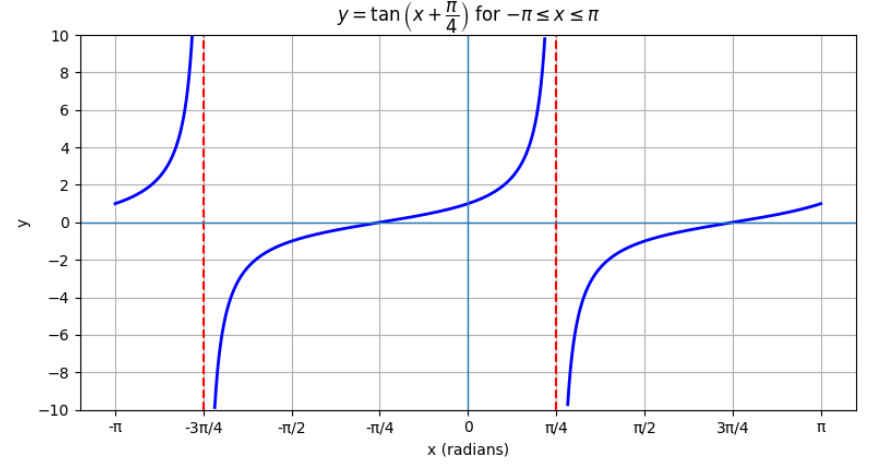
Sketch the graph of \(y = \tan\left(x + \dfrac{\pi}{4}\right)\) for \(-\pi \leq x \leq \pi\).
▶️ Answer/Explanation
Step 1: Recall tangent curve
The basic \(\tan x\) has asymptotes at \(x = \pm \dfrac{\pi}{2}, \pm \dfrac{3\pi}{2}, \dots\).
Step 2: Apply horizontal shift
\(y = \tan(x + \dfrac{\pi}{4})\) means a shift of \(-\dfrac{\pi}{4}\) to the left.
Step 3: New asymptotes
Original asymptotes: \(x = -\dfrac{\pi}{2}, \dfrac{\pi}{2}\). After shift: \(x = -\dfrac{\pi}{2} – \dfrac{\pi}{4} = -\dfrac{3\pi}{4}\), and \(x = \dfrac{\pi}{2} – \dfrac{\pi}{4} = \dfrac{\pi}{4}\).
Step 4: Key point
At \(x = -\dfrac{\pi}{4}\), \(y = \tan(0) = 0\).
Final Sketch: Tangent curve shifted left by \(\dfrac{\pi}{4}\), asymptotes at \(-\dfrac{3\pi}{4}\) and \(\dfrac{\pi}{4}\).
Exact Values of Standard Angles
Exact Values of Standard Angles
| Angle | Radians | \(\sin \theta\) | \(\cos \theta\) | \(\tan \theta\) |
|---|---|---|---|---|
| 0° | 0 | 0 | 1 | 0 |
| 30° | \(\dfrac{\pi}{6}\) | \(\dfrac{1}{2}\) | \(\dfrac{\sqrt{3}}{2}\) | \(\dfrac{1}{\sqrt{3}}\) |
| 45° | \(\dfrac{\pi}{4}\) | \(\dfrac{1}{\sqrt{2}}\) | \(\dfrac{1}{\sqrt{2}}\) | 1 |
| 60° | \(\dfrac{\pi}{3}\) | \(\dfrac{\sqrt{3}}{2}\) | \(\dfrac{1}{2}\) | \(\sqrt{3}\) |
| 90° | \(\dfrac{\pi}{2}\) | 1 | 0 | Not defined |
Using Related Angles (Unit Circle Symmetry)
- In Quadrant I, all trignometric ratios are positive.
- In Quadrant II, sine is positive, cosine and tangent are negative.
- In Quadrant III, tangent is positive, sine and cosine are negative.
- In Quadrant IV, cosine is positive, sine and tangent are negative.
Thus:
- \(\cos 150^\circ = -\dfrac{\sqrt{3}}{2}\) (since reference angle is \(30^\circ\), cos is negative in Quadrant II).
- \(\sin \dfrac{3\pi}{4} = \sin 135^\circ = \dfrac{1}{\sqrt{2}}\).
- \(\tan 225^\circ = 1\), since tangent is positive in Quadrant III with reference \(45^\circ\).
Example:
Find the exact values of \(\sin 120^\circ\), \(\cos 225^\circ\), and \(\tan 300^\circ\).
▶️ Answer/Explanation
Step 1: Identify reference angles
- \(120^\circ = 180^\circ – 60^\circ \) → reference angle \(60^\circ\).
- \(225^\circ = 180^\circ + 45^\circ \) → reference angle \(45^\circ\).
- \(300^\circ = 360^\circ – 60^\circ \) → reference angle \(60^\circ\).
Step 2: Apply quadrant signs
- Quadrant II → sine positive: \(\sin 120^\circ = \sin 60^\circ = \dfrac{\sqrt{3}}{2}\).
- Quadrant III → cosine negative: \(\cos 225^\circ = -\cos 45^\circ = -\dfrac{1}{\sqrt{2}}\).
- Quadrant IV → tangent negative: \(\tan 300^\circ = -\tan 60^\circ = -\sqrt{3}\).
Final Answers:
- \(\sin 120^\circ = \dfrac{\sqrt{3}}{2}\)
- \(\cos 225^\circ = -\dfrac{1}{\sqrt{2}}\)
- \(\tan 300^\circ = -\sqrt{3}\)
Example:
Find the exact values of \(\cos 240^\circ\), \(\sin \dfrac{7\pi}{6}\), and \(\tan 135^\circ\).
▶️ Answer/Explanation
Step 1: Identify reference angles
- \(240^\circ = 180^\circ + 60^\circ\) → reference angle \(60^\circ\).
- \(\dfrac{7\pi}{6} = 210^\circ = 180^\circ + 30^\circ\) → reference angle \(30^\circ\).
- \(135^\circ = 180^\circ – 45^\circ\) → reference angle \(45^\circ\).
Step 2: Apply quadrant signs
- Quadrant III → cosine negative: \(\cos 240^\circ = -\cos 60^\circ = -\dfrac{1}{2}\).
- Quadrant III → sine negative: \(\sin \dfrac{7\pi}{6} = -\sin 30^\circ = -\dfrac{1}{2}\).
- Quadrant II → tangent negative: \(\tan 135^\circ = -\tan 45^\circ = -1\).
Final Answers:
- \(\cos 240^\circ = -\dfrac{1}{2}\)
- \(\sin \dfrac{7\pi}{6} = -\dfrac{1}{2}\)
- \(\tan 135^\circ = -1\)
Inverse Trigonometric Functions and Principal Values
Inverse Trigonometric Functions and Principal Values
We use the notations \(\sin^{-1}x\), \(\cos^{-1}x\), and \(\tan^{-1}x\) to denote the principal values of the inverse trigonometric functions. These are defined with restricted ranges so that each inverse is a single-valued function.
Sine inverse:
\(\sin^{-1}x = \theta \quad \Rightarrow \quad \sin \theta = x, \; -1 \leq x \leq 1, \; \theta \in \left[-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right]\).
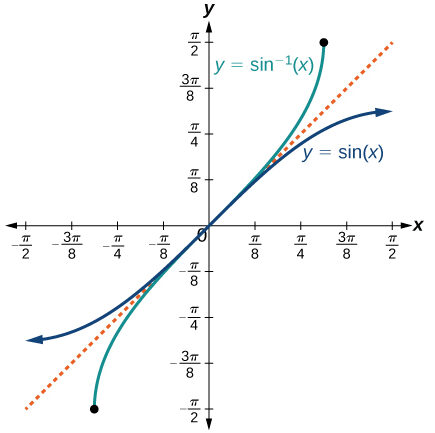
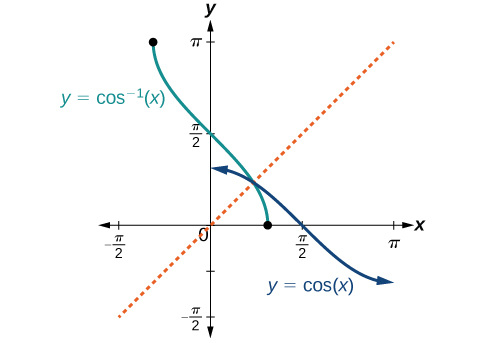
Cosine inverse:
\(\cos^{-1}x = \theta \quad \Rightarrow \quad \cos \theta = x, \; -1 \leq x \leq 1, \; \theta \in [0, \pi]\).
Tangent inverse:
\(\tan^{-1}x = \theta \quad \Rightarrow \quad \tan \theta = x, \; -\infty < x < \infty, \; \theta \in \left(-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right)\).
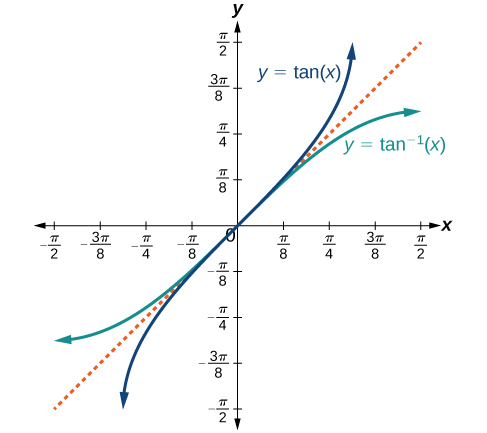
Important: The ranges are chosen so that each function is one-to-one and hence invertible.
Example:
Evaluate \(\sin^{-1}\left(-\dfrac{\sqrt{3}}{2}\right)\).
▶️ Answer/Explanation
Step 1: Recall definition
\(\sin^{-1}x\) gives the angle \(\theta \in \left[-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right]\) such that \(\sin \theta = x\).
Step 2: Identify value
\(\sin \theta = -\dfrac{\sqrt{3}}{2} \implies \theta = -\dfrac{\pi}{3}\) (since it must lie in the range \([-90^\circ, 90^\circ]\)).
Answer: \(\sin^{-1}\left(-\dfrac{\sqrt{3}}{2}\right) = -\dfrac{\pi}{3}\).
Example:
Evaluate \(\cos^{-1}\left(-\dfrac{1}{2}\right)\).
▶️ Answer/Explanation
Step 1: Recall definition
\(\cos^{-1}x\) gives the angle \(\theta \in [0, \pi]\) such that \(\cos \theta = x\).
Step 2: Identify value
\(\cos \theta = -\dfrac{1}{2} \implies \theta = \dfrac{2\pi}{3}\).
Answer: \(\cos^{-1}\left(-\dfrac{1}{2}\right) = \dfrac{2\pi}{3}\).
Example:
Evaluate \(\tan^{-1}(-1)\).
▶️ Answer/Explanation
Step 1: Recall definition
\(\tan^{-1}x\) gives the angle \(\theta \in \left(-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right)\) such that \(\tan \theta = x\).
Step 2: Identify value
\(\tan \theta = -1 \implies \theta = -\dfrac{\pi}{4}\).
Answer: \(\tan^{-1}(-1) = -\dfrac{\pi}{4}\).
Fundamental Trigonometric Identities
Fundamental Trigonometric Identities
Two of the most important trigonometric identities are:
1. \(\tan x = \dfrac{\sin x}{\cos x}, \quad \cos x \neq 0\)
2. \(\sin^2 x + \cos^2 x = 1\)
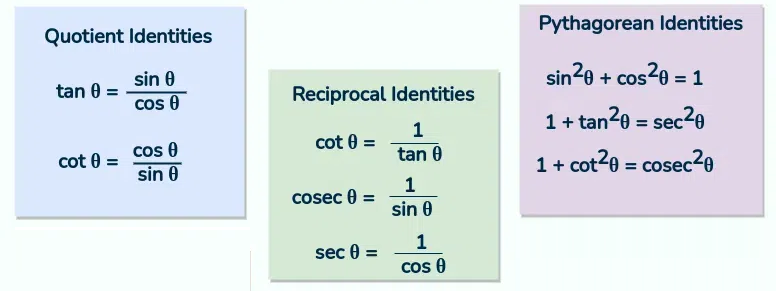
These identities are frequently used to:
- Prove other trigonometric identities
- Simplify trigonometric expressions
- Solve trigonometric equations
Example:
Prove that \(\dfrac{1 – \cos^2 x}{\cos x} = \tan x \sin x\).
▶️ Answer/Explanation
Step 1: Start with the left-hand side (LHS)
\(\dfrac{1 – \cos^2 x}{\cos x}\).
Step 2: Use Pythagoras identity
\(1 – \cos^2 x = \sin^2 x\).
LHS = \(\dfrac{\sin^2 x}{\cos x}\).
Step 3: Rewrite using \(\tan x\)
\(\dfrac{\sin^2 x}{\cos x} = \sin x \cdot \dfrac{\sin x}{\cos x} = \sin x \cdot \tan x\).
Answer: LHS = RHS, hence proven
Example :
Simplify: \(\dfrac{\tan^2 x + 1}{\sec^2 x}\).
▶️ Answer/Explanation
Step 1: Recall identities
\(\tan^2 x + 1 = \sec^2 x\).
Step 2: Substitute
\(\dfrac{\tan^2 x + 1}{\sec^2 x} = \dfrac{\sec^2 x}{\sec^2 x} = 1\).
Answer: Simplified expression = 1
Example :
Solve for \(0 \leq x \leq 2\pi\): \(\sin^2 x = \cos^2 x\).
▶️ Answer/Explanation
Step 1: Rewrite equation
\(\sin^2 x = \cos^2 x \implies \dfrac{\sin^2 x}{\cos^2 x} = 1\).
\(\tan^2 x = 1\).
Step 2: Solve
\(\tan x = \pm 1\).
So \(x = \dfrac{\pi}{4}, \dfrac{3\pi}{4}, \dfrac{5\pi}{4}, \dfrac{7\pi}{4}\).
Answer: \(x = \dfrac{\pi}{4}, \dfrac{3\pi}{4}, \dfrac{5\pi}{4}, \dfrac{7\pi}{4}\).
Solving Simple Trigonometric Equations in a Specified Interval
Solving Simple Trigonometric Equations in a Specified Interval
When solving equations involving sine, cosine, or tangent, we often look for solutions only within a given interval, such as \(0 \leq x \leq 2\pi\) or \(0^\circ \leq \theta \leq 360^\circ\).
Steps to Solve:
- Isolate the trigonometric function (sin, cos, tan).
- Find the principal solution using inverse functions (\(\sin^{-1}, \cos^{-1}, \tan^{-1}\)).
- Determine all other solutions within the interval using the symmetry of the trig graph (CAST rule / unit circle).
- Write the complete set of solutions in the specified interval.
Example:
Solve for \(0 \leq x \leq 2\pi\): \(\sin x = \dfrac{\sqrt{3}}{2}\).
▶️ Answer/Explanation
Step 1: Principal solution
\(\sin^{-1}\left(\dfrac{\sqrt{3}}{2}\right) = \dfrac{\pi}{3}\).
Step 2: Other solutions
Sine is positive in Quadrant I and II.
So solutions are \(x = \dfrac{\pi}{3}, \; \pi – \dfrac{\pi}{3} = \dfrac{2\pi}{3}\).
Answer: \(x = \dfrac{\pi}{3}, \dfrac{2\pi}{3}\).
Example:
Solve for \(0^\circ \leq \theta \leq 360^\circ\): \(\cos \theta = -\dfrac{1}{2}\).
▶️ Answer/Explanation
Step 1: Principal solution
\(\cos^{-1}\left(\dfrac{1}{2}\right) = 60^\circ\).
Step 2: Adjust for negative cosine
Cosine is negative in Quadrant II and III.
So solutions are \(\theta = 180^\circ – 60^\circ = 120^\circ\), and \(\theta = 180^\circ + 60^\circ = 240^\circ\).
Answer: \(\theta = 120^\circ, 240^\circ\).
Example:
Solve for \(0 \leq x \leq 2\pi\): \(\tan x = 1\).
▶️ Answer/Explanation
Step 1: Principal solution
\(\tan^{-1}(1) = \dfrac{\pi}{4}\).
Step 2: Other solutions
Tangent is positive in Quadrant I and III.
So solutions are \(x = \dfrac{\pi}{4}, \; \pi + \dfrac{\pi}{4} = \dfrac{5\pi}{4}\).
Answer: \(x = \dfrac{\pi}{4}, \dfrac{5\pi}{4}\).
