CIE AS/A Level Maths-2.5 Integration- Study Notes- New Syllabus - 2026-2027
CIE AS/A Level Maths-2.5 Integration- Study Notes- New Syllabus
Ace AS/A Level Maths Exam with CIE AS/A Level Maths-2.5 Integration- Study Notes
Key Concepts:
- Integration as Reverse Differentiation (Extended Forms)
- Integration Using Trigonometric Identities
- Trapezium Rule for Estimating Definite Integrals
Integration as Reverse Differentiation (Extended Forms)
Integration as Reverse Differentiation (Extended Forms)
We can integrate many functions by recognizing them as the result of differentiating a simple composite function. This is sometimes called reverse differentiation.

| Function | Integral |
|---|---|
| Exponential | \(\displaystyle \int e^{ax+b} \, dx = \dfrac{1}{a} e^{ax+b} + C, \; a \neq 0\) |
| Reciprocal Linear | \(\displaystyle \int \dfrac{1}{ax+b} \, dx = \dfrac{1}{a} \ln|ax+b| + C\) |
| Sine | \(\displaystyle \int \sin(ax+b) \, dx = -\dfrac{1}{a} \cos(ax+b) + C\) |
| Cosine | \(\displaystyle \int \cos(ax+b) \, dx = \dfrac{1}{a} \sin(ax+b) + C\) |
| Secant Squared | \(\displaystyle \int \sec^2(ax+b) \, dx = \dfrac{1}{a} \tan(ax+b) + C\) |
Example:
Evaluate \(\displaystyle \int e^{5x+2} \, dx\).
▶️Answer/Explanation
\(\int e^{5x+2} dx = \dfrac{1}{5} e^{5x+2} + C\).
Example:
Evaluate \(\displaystyle \int \dfrac{1}{3x-1} \, dx\).
▶️Answer/Explanation
\(\int \dfrac{1}{3x-1} dx = \dfrac{1}{3}\ln|3x-1| + C\).
Example:
Evaluate \(\displaystyle \int \sin(2x+5) \, dx\).
▶️Answer/Explanation
\(\int \sin(2x+5) dx = -\dfrac{1}{2}\cos(2x+5) + C\).
Example:
Evaluate \(\displaystyle \int \cos(4x) \, dx\).
▶️Answer/Explanation
\(\int \cos(4x) dx = \dfrac{1}{4}\sin(4x) + C\).
Example:
Evaluate \(\displaystyle \int \sec^2(3x) \, dx\).
▶️Answer/Explanation
\(\int \sec^2(3x) dx = \dfrac{1}{3}\tan(3x) + C\).
Integration Using Trigonometric Identities
Integration Using Trigonometric Identities
Sometimes, integrals of trigonometric functions cannot be evaluated directly, but can be simplified using standard trigonometric identities. The most common identities used are:
Double-angle identities:

\(\sin(2x) = 2\sin x \cos x\)
\(\cos(2x) = \cos^2 x – \sin^2 x = 2\cos^2 x – 1 = 1 – 2\sin^2 x\)
Power-reduction (half-angle) identities:

\(\sin^2 x = \dfrac{1 – \cos(2x)}{2}\)
\(\cos^2 x = \dfrac{1 + \cos(2x)}{2}\)
These allow us to transform squares of trig functions or integrals into simpler forms.
Example:
Evaluate \(\displaystyle \int \sin(2x) \, dx\).
▶️Answer/Explanation
We can integrate directly:
\(\int \sin(2x) dx = -\dfrac{1}{2}\cos(2x) + C\).
No identity was required, but it is a direct use of the double-angle formula.
Example:
Evaluate \(\displaystyle \int \cos^2(2x) \, dx\).
▶️Answer/Explanation
Step 1: Use the identity \(\cos^2 \theta = \dfrac{1 + \cos(2\theta)}{2}\).
\(\cos^2(2x) = \dfrac{1 + \cos(4x)}{2}\).
Step 2: Substitute into the integral.
\(\int \cos^2(2x) dx = \int \dfrac{1 + \cos(4x)}{2} dx\).
= \(\dfrac{1}{2}\int 1 dx + \dfrac{1}{2}\int \cos(4x) dx\).
= \(\dfrac{x}{2} + \dfrac{1}{8}\sin(4x) + C\).
Example:
Evaluate \(\displaystyle \int \sin^2(x) \, dx\).
▶️Answer/Explanation
Step 1: Use the identity \(\sin^2 x = \dfrac{1 – \cos(2x)}{2}\).
\(\int \sin^2(x) dx = \int \dfrac{1 – \cos(2x)}{2} dx\).
Step 2: Split into two parts.
= \(\dfrac{1}{2}\int 1 dx – \dfrac{1}{2}\int \cos(2x) dx\).
= \(\dfrac{x}{2} – \dfrac{1}{4}\sin(2x) + C\).
Example:
Evaluate \(\displaystyle \int \sin x \cos x \, dx\).
▶️Answer/Explanation
Step 1: Use the identity \(\sin x \cos x = \dfrac{1}{2}\sin(2x)\).
\(\int \sin x \cos x dx = \int \dfrac{1}{2}\sin(2x) dx\).
= \(-\dfrac{1}{4}\cos(2x) + C\).
Trapezium Rule for Estimating Definite Integrals
Trapezium Rule for Estimating Definite Integrals
The trapezium rule is a method of approximating the value of a definite integral \(\displaystyle \int_a^b f(x) \, dx\) by dividing the interval \([a, b]\) into smaller sub-intervals and approximating the area under the curve with trapezia (trapezoids).
Step 1: Divide the interval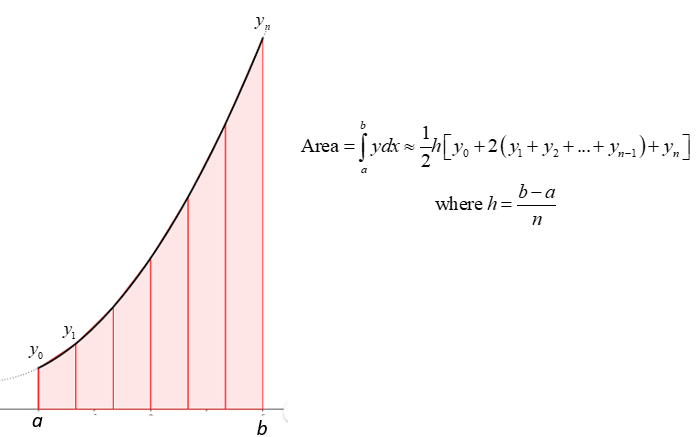
Let \([a, b]\) be divided into \(n\) equal sub-intervals, each of width \(h = \dfrac{b-a}{n}\). Then the points are:
\(x_0 = a, x_1 = a+h, x_2 = a+2h, \dots, x_n = b\)
Step 2: Apply the trapezium rule formula
The trapezium rule formula is:
\(\displaystyle \int_a^b f(x) \, dx \approx \dfrac{h}{2} \Big[f(x_0) + 2f(x_1) + 2f(x_2) + \dots + 2f(x_{n-1}) + f(x_n)\Big]\)
Here:
- \(f(x_0)\) and \(f(x_n)\) are the function values at the endpoints.
- \(f(x_1), f(x_2), \dots, f(x_{n-1})\) are the function values at the intermediate points, each multiplied by 2.
Step 3: Calculate the approximation
1. Find \(h = \dfrac{b-a}{n}\).
2. Calculate \(f(x_i)\) at each \(x_i\).
3. Apply the formula to find the approximate integral.
Example:
Estimate \(\displaystyle \int_0^2 (x^2+1) \, dx\) using the trapezium rule with \(n = 4\).
▶️Answer/Explanation
Solution:
Step 1: \(h = \dfrac{2-0}{4} = 0.5\)
Step 2: Divide interval: \(x_0=0, x_1=0.5, x_2=1, x_3=1.5, x_4=2\)
Step 3: Compute \(f(x_i)\): \(f(0)=1, f(0.5)=1.25, f(1)=2, f(1.5)=3.25, f(2)=5\)
Step 4: Apply formula:
\(\dfrac{0.5}{2}[1 + 2(1.25 + 2 + 3.25) + 5] = 0.25 [1 + 2(6.5) + 5] = 0.25[1 + 13 + 5] = 0.25[19] = 4.75\)
So, the approximate value of the integral is 4.75.
Over- or Under-estimate Using Graphs
To determine whether the trapezium rule gives an over- or under-estimate:
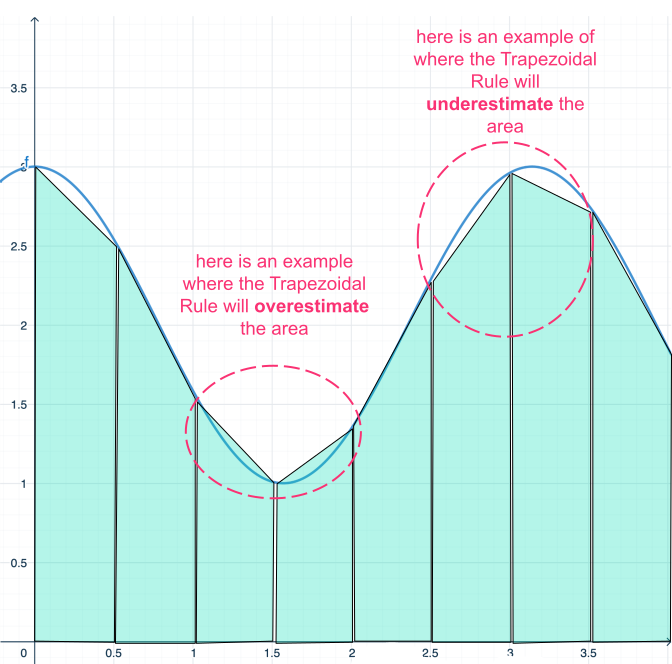
- If the function \(f(x)\) is concave upwards (\(f”(x) > 0\)), the trapezium rule underestimates the integral.
- If the function \(f(x)\) is concave downwards (\(f”(x) < 0\)), the trapezium rule overestimates the integral.
This is because the trapezia either lie below (concave up) or above (concave down) the curve.
Example:
Consider \(\displaystyle \int_0^1 e^x \, dx\) with \(n=2\). Is it Over- or Under-estimate?
▶️Answer/Explanation
Solution:
Function \(f(x) = e^x\) is concave upwards (\(f”(x) = e^x > 0\)), so the trapezium rule will underestimate the integral.
Step 1: \(h = \dfrac{1-0}{2} = 0.5\)
Step 2: \(x_0=0, x_1=0.5, x_2=1\)
Step 3: \(f(0)=1, f(0.5)\approx1.6487, f(1)\approx2.7183\)
Step 4: Trapezium rule:
\(\dfrac{0.5}{2}[1 + 2(1.6487) + 2.7183] = 0.25[1 + 3.2974 + 2.7183] = 0.25[7.0157] \approx 1.754\)
Exact integral: \(e – 1 \approx 1.718\). Here, the trapezium approximation slightly overestimates due to small \(n\), but for concave upwards and large \(n\), it generally underestimates.
