CIE AS/A Level Maths-3.3 Trigonometry- Study Notes- New Syllabus - 2026-2027
CIE AS/A Level Maths-3.3 Trigonometry- Study Notes- New Syllabus
Ace AS/A Level Maths Exam with CIE AS/A Level Maths-3.3 Trigonometry- Study Notes
Key Concepts:
- Secant, Cosecant, and Cotangent Functions
- Trigonometric Identities
Secant, Cosecant, and Cotangent Functions
Secant, Cosecant, and Cotangent Functions
Definitions (in terms of sine, cosine, tangent):
- Secant: \(\sec x = \dfrac{1}{\cos x}\)
- Cosecant: \(\csc x = \dfrac{1}{\sin x}\)
- Cotangent: \(\cot x = \dfrac{1}{\tan x} = \dfrac{\cos x}{\sin x}\)
Properties:
- Domain & Range:
- \(\sec x\) is undefined where \(\cos x = 0 \Rightarrow x = \frac{\pi}{2} + n\pi\)
- \(\csc x\) is undefined where \(\sin x = 0 \Rightarrow x = n\pi\)
- \(\cot x\) is undefined where \(\tan x = 0 \Rightarrow x = n\pi\)
- Periodicity:
- \(\sec x\) and \(\csc x\) have period \(2\pi\)
- \(\cot x\) has period \(\pi\)
- Symmetry:
- \(\sec(-x) = \sec x\) (even)
- \(\csc(-x) = -\csc x\) (odd)
- \(\cot(-x) = -\cot x\) (odd)
Graphs:
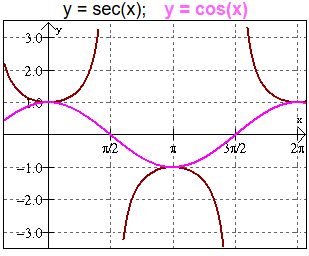
- \(\sec x\) has vertical asymptotes where \(\cos x = 0\); branches open upwards or downwards depending on sign of \(\cos x\).
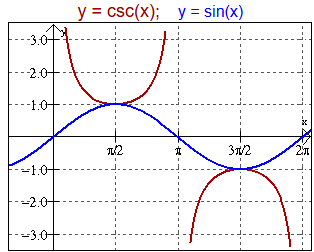
- \(\csc x\) has vertical asymptotes where \(\sin x = 0\); branches open upwards or downwards depending on sign of \(\sin x\).
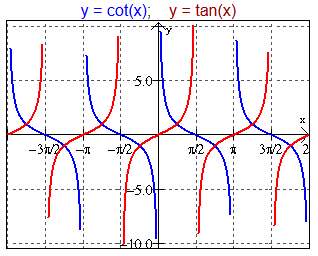
- \(\cot x\) has vertical asymptotes where \(\sin x = 0\); decreases from \(+\infty\) to \(-\infty\) in one period.
Example
Find the exact value of \(\sec 75^\circ\) using known angles.
▶️ Answer / Explanation
Step 1: Express secant in terms of cosine:
\(\sec 75^\circ = \dfrac{1}{\cos 75^\circ}\)
Step 2: Use the sum formula for cosine:
\(\cos(75^\circ) = \cos(45^\circ + 30^\circ) = \cos 45^\circ \cos 30^\circ – \sin 45^\circ \sin 30^\circ\)
\(\cos 45^\circ = \dfrac{\sqrt{2}}{2}, \cos 30^\circ = \dfrac{\sqrt{3}}{2}, \sin 45^\circ = \dfrac{\sqrt{2}}{2}, \sin 30^\circ = \dfrac{1}{2}\)
\(\cos 75^\circ = \dfrac{\sqrt{2}}{2} \cdot \dfrac{\sqrt{3}}{2} – \dfrac{\sqrt{2}}{2} \cdot \dfrac{1}{2} = \dfrac{\sqrt{6}}{4} – \dfrac{\sqrt{2}}{4} = \dfrac{\sqrt{6} – \sqrt{2}}{4}\)
Step 3: Find secant:
\(\sec 75^\circ = \dfrac{1}{\cos 75^\circ} = \dfrac{4}{\sqrt{6} – \sqrt{2}}\)
Step 4: Rationalise the denominator:
\(\sec 75^\circ = \dfrac{4(\sqrt{6} + \sqrt{2})}{(\sqrt{6} – \sqrt{2})(\sqrt{6} + \sqrt{2})} = \dfrac{4(\sqrt{6} + \sqrt{2})}{6 – 2} = \dfrac{4(\sqrt{6} + \sqrt{2})}{4} = \sqrt{6} + \sqrt{2}\)
Final Answer:
\(\boxed{\sec 75^\circ = \sqrt{6} + \sqrt{2}}\)
Example
Solve for \(x\) in \([0, 2\pi]\): \(\csc x = 2\)
▶️ Answer / Explanation
Step 1: Express in terms of sine:
\(\csc x = \dfrac{1}{\sin x} = 2 \Rightarrow \sin x = \dfrac{1}{2}\)
Step 2: Solve for \(x\) in \([0, 2\pi]\):
\(\sin x = \dfrac{1}{2} \Rightarrow x = \dfrac{\pi}{6}, \dfrac{5\pi}{6}\)
Final Answer:
\(\boxed{x = \dfrac{\pi}{6}, \dfrac{5\pi}{6}}\)
Example
Solve: \(\cot 2x = 1\) in \([0, 2\pi]\)
▶️ Answer / Explanation
Step 1: Express in terms of tangent: \(\cot 2x = \dfrac{1}{\tan 2x} = 1 \Rightarrow \tan 2x = 1\)
Step 2: Solve for \(2x\):
\(\tan 2x = 1 \Rightarrow 2x = \dfrac{\pi}{4} + n\pi, n \in \mathbb{Z}\)
Step 3: Solve for \(x\) in \([0, 2\pi]\):
\(x = \dfrac{\pi}{8} + n\dfrac{\pi}{2}\)
Values in \([0, 2\pi]\): \(x = \dfrac{\pi}{8}, \dfrac{5\pi}{8}, \dfrac{9\pi}{8}, \dfrac{13\pi}{8}\)
Final Answer:
\(\boxed{x = \dfrac{\pi}{8}, \dfrac{5\pi}{8}, \dfrac{9\pi}{8}, \dfrac{13\pi}{8}}\)
Trigonometric Identities
Trigonometric Identities
Pythagorean Identities:
\(\sin^2\theta + \cos^2\theta = 1\)
\(\sec^2\theta = 1 + \tan^2\theta\)
\(\csc^2\theta = 1 + \cot^2\theta\)
Angle Addition/Subtraction:
\(\sin(A \pm B) = \sin A \cos B \pm \cos A \sin B\)
\(\cos(A \pm B) = \cos A \cos B \mp \sin A \sin B\)
\(\tan(A \pm B) = \dfrac{\tan A \pm \tan B}{1 \mp \tan A \tan B}\)
Double Angle Formulas:
\(\sin 2A = 2 \sin A \cos A\)
\(\cos 2A = \cos^2 A – \sin^2 A = 2 \cos^2 A – 1 = 1 – 2 \sin^2 A\)
\(\tan 2A = \dfrac{2 \tan A}{1 – \tan^2 A}\)
Sum-to-Product (or Amplitude-Phase) Form:
\(a \sin\theta + b \cos\theta = R \sin(\theta + \alpha)\) where \(R = \sqrt{a^2+b^2}, \tan \alpha = \dfrac{b}{a}\)
\(a \sin\theta + b \cos\theta = R \cos(\theta – \beta)\) where \(R = \sqrt{a^2+b^2}, \tan \beta = \dfrac{a}{b}\)

Example
Simplify \(\cos(x – 30^\circ) – 3 \sin(x – 60^\circ)\)
▶️ Answer / Explanation
Step 1: Expand both terms using \(\cos(A-B)\) and \(\sin(A-B)\) formulas:
\(\cos(x – 30^\circ) = \cos x \cos 30^\circ + \sin x \sin 30^\circ = \cos x \frac{\sqrt{3}}{2} + \sin x \frac{1}{2}\)
\(\sin(x – 60^\circ) = \sin x \cos 60^\circ – \cos x \sin 60^\circ = \sin x \frac{1}{2} – \cos x \frac{\sqrt{3}}{2}\)
Step 2: Multiply by -3:
\(-3 \sin(x – 60^\circ) = -3(\frac{1}{2} \sin x – \frac{\sqrt{3}}{2} \cos x) = -\frac{3}{2} \sin x + \frac{3\sqrt{3}}{2} \cos x\)
Step 3: Combine terms:
\(\cos(x-30^\circ) – 3 \sin(x-60^\circ) = (\frac{\sqrt{3}}{2} + \frac{3\sqrt{3}}{2})\cos x + (\frac{1}{2} – \frac{3}{2}) \sin x = 2\sqrt{3} \cos x – \sin x\)
Step 4: Optional: express in amplitude-phase form:
\(R = \sqrt{(2\sqrt{3})^2 + (-1)^2} = \sqrt{12 + 1} = \sqrt{13}\)
\(\tan \alpha = \dfrac{-1}{2\sqrt{3}} \Rightarrow \alpha = -\arctan(\frac{1}{2\sqrt{3}})\)
Final Answer: \(2\sqrt{3} \cos x – \sin x = \sqrt{13} \cos(x + \arctan(\frac{1}{2\sqrt{3}}))\)
Example
Solve: \(\sec^2 \theta – \tan^2 \theta = 5\)
▶️ Answer / Explanation
Step 1: Recall identity: \(\sec^2 \theta – \tan^2 \theta = 1\)
Step 2: But given equation says \(\sec^2 \theta – \tan^2 \theta = 5\). Since identity is always 1, there is no solution.
Final Answer: No solution.
Example
Solve: \(\tan\theta + \cot\theta = 4\) for \(0 < \theta < \frac{\pi}{2}\)
▶️ Answer / Explanation
Step 1: Express \(\cot\theta = \frac{1}{\tan\theta}\):
\(\tan\theta + \frac{1}{\tan\theta} = 4 \Rightarrow \frac{\tan^2 \theta + 1}{\tan \theta} = 4\)
Step 2: Multiply both sides by \(\tan\theta\):
\(\tan^2 \theta + 1 = 4 \tan \theta \Rightarrow \tan^2 \theta – 4\tan\theta + 1 = 0\)
Step 3: Solve quadratic for \(\tan\theta\):
\(\tan\theta = \frac{4 \pm \sqrt{16 – 4}}{2} = \frac{4 \pm \sqrt{12}}{2} = 2 \pm \sqrt{3}\)
Step 4: Choose solution in \(0 < \theta < \frac{\pi}{2}\) (tan > 0):
\(\theta = \arctan(2 + \sqrt{3})\) or \(\theta = \arctan(2 – \sqrt{3})\)
Final Answer: \(\boxed{\theta = \arctan(2 + \sqrt{3}), \arctan(2 – \sqrt{3})}\)
