CIE AS/A Level Maths-6.2 Linear combinations of random variables- Study Notes- New Syllabus - 2026-2027
CIE AS/A Level Maths-6.2 Linear combinations of random variables- Study Notes- New Syllabus
Ace AS/A Level Maths Exam with CIE AS/A Level Maths-6.2 Linear combinations of random variables- Study Notes
Key Concepts:
- Linear Combinations of Random Variables
Linear Combinations of Random Variables
Linear Combinations of Random Variables
Expectation and variance for a linear transformation:
If \(X\) is a random variable and \(a, b\) are constants:
\( \mathrm{E}(aX + b) = a\mathrm{E}(X) + b \)
\( \mathrm{Var}(aX + b) = a^2 \mathrm{Var}(X) \)4
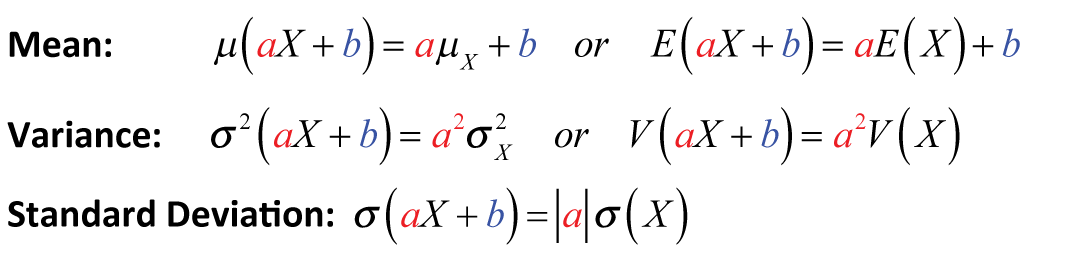
Expectation and variance for a linear combination of independent variables:
If \(X\) and \(Y\) are independent random variables and \(a, b\) are constants:
\( \mathrm{E}(aX + bY) = a \mathrm{E}(X) + b \mathrm{E}(Y) \)
\( \mathrm{Var}(aX + bY) = a^2 \mathrm{Var}(X) + b^2 \mathrm{Var}(Y) \)
Distribution properties:
- If \(X \sim N(\mu, \sigma^2)\), then \(aX + b \sim N(a\mu + b, a^2 \sigma^2)\)
- If \(X \sim N(\mu_X, \sigma_X^2)\) and \(Y \sim N(\mu_Y, \sigma_Y^2)\) are independent, then \(aX + bY \sim N(a\mu_X + b\mu_Y, a^2 \sigma_X^2 + b^2 \sigma_Y^2)\)
- If \(X \sim \text{Po}(\lambda_1)\) and \(Y \sim \text{Po}(\lambda_2)\) are independent, then \(X + Y \sim \text{Po}(\lambda_1 + \lambda_2)\)
Example:
A factory produces an average of 5 defective items per day, \(X \sim \text{Po}(5)\). Let \(Y = 2X + 3\). Find \(\mathrm{E}(Y)\) and \(\mathrm{Var}(Y)\).
▶️ Answer/Explanation
\(\mathrm{E}(Y) = \mathrm{E}(2X + 3) = 2 \mathrm{E}(X) + 3 = 2(5) + 3 = 13\)
\(\mathrm{Var}(Y) = \mathrm{Var}(2X + 3) = 2^2 \mathrm{Var}(X) = 4 \cdot 5 = 20\)
Final Answer: \(\boxed{\mathrm{E}(Y) = 13, \; \mathrm{Var}(Y) = 20}\)
Example:
Let \(X \sim N(10, 4)\) and \(Y \sim N(20, 9)\) be independent. Find the distribution of \(Z = 3X – 2Y\).
▶️ Answer/Explanation
Mean: \(\mathrm{E}(Z) = 3 \mathrm{E}(X) – 2 \mathrm{E}(Y) = 3(10) – 2(20) = 30 – 40 = -10\)
Variance: \(\mathrm{Var}(Z) = 3^2 \mathrm{Var}(X) + (-2)^2 \mathrm{Var}(Y) = 9 \cdot 4 + 4 \cdot 9 = 36 + 36 = 72\)
Distribution: \(Z \sim N(-10, 72)\)
Final Answer: \(\boxed{Z \sim N(-10, 72)}\)
Example:
Two independent call centers receive on average 4 and 6 calls per hour, respectively. Let \(X \sim \text{Po}(4)\) and \(Y \sim \text{Po}(6)\). Find the distribution of total calls \(T = X + Y\).
▶️ Answer/Explanation
For independent Poisson variables: \(X + Y \sim \text{Po}(\lambda_X + \lambda_Y)\)
\(T \sim \text{Po}(4 + 6) = \text{Po}(10)\)
Final Answer: \(\boxed{T \sim \text{Po}(10)}\)
