Question
A student conducts an experiment to investigate which cell shape
would allow for the most efficient exchange of materials with its environment. Agar blocks (containing bromothymol blue dye) are cut
into three different shapes to model three differently shaped cells. The
agar blocks are then placed in a vinegar solution. As the vinegar
diffuses into the agar models, the acid in the vinegar will turn the
bromothymol blue dye yellow. The time required for each agar model
to turn completely yellow is measured and is an indication of the
efficiency of movement of materials into the agar models. The shape,
volume, and surface area of each agar block is shown in the table.
| Shape | Volume | Surface Area |
| Cylinder | 25.1 \(cm^3\) | 50.2 \(cm^2\) |
| Sphere | 33.5 \(cm^3\) | 50.2 \(cm^2\) |
| Cube | 8 \(cm^3\) | 24 \(cm^2\) |
(a) Describe the measurement that would best predict the efficiency
of each agar block’s exchange of materials with its environment.
Calculate that measurement for each agar block.
(b) Identify the independent variable and the dependent variable in
this experiment.
(c) Predict which cell would turn completely yellow first.
(d) Justify your prediction from part (c).
▶️Answer/Explanation
Ans:
(a) The measurement that would best predict the efficiency of each
agar block’s exchange of materials with its environment is the
surface area to volume ratio. For the cylinder, the ratio is \(\frac{50.2}{25.1}=2\). For the sphere, the ratio is \(\frac{50.2}{33.5}=1.5\). For the cube, the ratio is \(\frac{24}{8}=3\).
(b) The independent variable is the shape of the agar block. The
dependent variable is the time it takes for the vinegar to diffuse
completely into the cell and turn it yellow.
(c) The cube would turn completely yellow first.
(d) The greater a cell’s surface area to volume ratio, the more
efficiently it will exchange materials with its environment. Since
the cube has the greatest surface area to volume ratio, it will
exchange materials the most efficiently and turn completely yellow
first.
Question
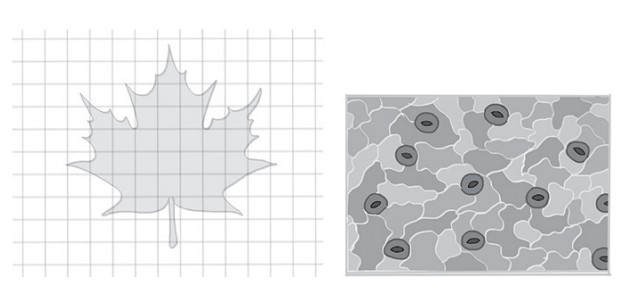
Estimate the area of the leaf above. Provide a brief description of your method. Assume each square is 1 \(cm^2\)
▶️Answer/Explanation
Ans:
There are several strategies you can use to estimate the leaf surface area.
A simple and fairly accurate way is as follows:
(1) Count the number of boxes that are at least 2/3 of the area covered by the leaf.
~25 ∴ ~25 \(cm^2\)
(2) Count the number boxes where approximately 1⁄2 of the box is
covered; then divide by 2 (2 boxes will contain approximately 1 cm2
of surface).
8/2 = 4 \(cm^2\)
(3) Count the number of boxes that have 1⁄4 or less covered; then divide
by 4.
20/4 = 5 \(cm^2\)
TOTAL = 25 \(cm^2\) + 4 \(cm^2\) + 5 \(cm^2\) = 34 \(cm^2\)
Question
Calculate the stomatal density of the section of leaf shown on the right (the section provided is 2 mm × 1.5 mm) and use it to estimate
the number of stomata on the leaf on the left. Assume stomatal density is constant.
▶️Answer/Explanation
Ans:
The section contains 9 full stomata and 2 stomata that look like there is
50% or more in the section. Depending on your method you may count each
as a full stomata or combine the two into one based on surface of stomata.
Either method is acceptable. Here, assume each stomata individually ∴ 11
stomata.
The area of the leaf shown is 2 mm × 1.5 mm = 3 \(mm^2\).
\(\frac{11 stomata}{3 mm^2} = \frac{3.7 stomata}{mm^2}\)
The leaf has 34 \(cm^2\) of area (from answer 55).
Assume only bottom surface has stomata.
\(1 cm^2 = 10 mm × 10 mm = 100 mm^2\)
34 \(cm^2\) × 3,400 \(mm^2\) = 12,580 stomata
