Question
![]()
A -2
B 0
C 2
D nonexistent
▶️Answer/Explanation
Ans:B
The numerator of \(\frac{10-6x^{2}}{5+3e^{x}}\) is a translated power function and the denominator is a translated exponential function. Since the exponential function \(e^{x}\) grows faster than the power function \(x^{2}\) , the relative magnitude of the denominator compared to the numerator will result in this expression converging to 0
as x
goes to infinity.
Question
The graph of which of the following equations has y =1 as an asymptote?
(A) y = lnx (B) y= sinx (C)\(y=\frac{x}{x+1}\) (D)\(\frac{x^{2}}{x-1}\) (E)\(y=e^{-x}\)
▶️Answer/Explanation
Ans:C
Question
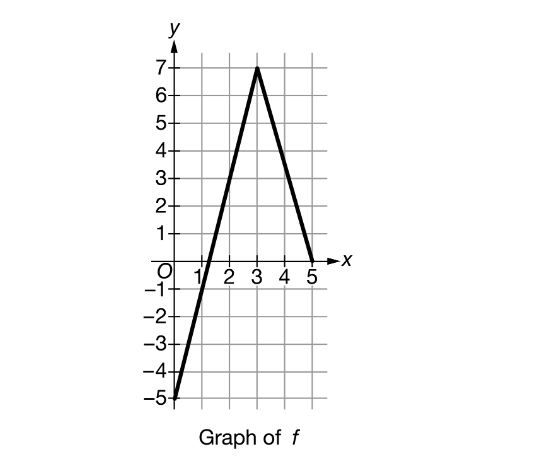
The graph of a function f is shown above. If
is the function defined by \( g(x)=\frac{x^{2}+1}{f(x)}\),what is the value of g′(2)?
A \(-\frac{8}{9}\)
B \(\frac{1}{9}\)
C 1
D \(\frac{32}{9}\)
▶️Answer/Explanation
Ans:A
The derivative of g
is found using the quotient rule.
\(g'(x)=\frac{2xf(x)-f'(x)(x^{2}+1)}{(f(x))^{2}}\)
The graph of f is used to determine that f(2)=3 and \(f'(2)=\frac{7-3}{3-2}=4\)Then \(g'(2)=\frac{4f(2)-f'(2)(5)}{(f(2))^{2}}=\frac{4(3)-4(5)}{9}=-\frac{8}{9}\)
Question
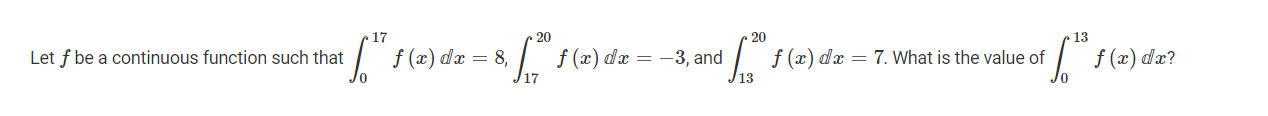
A -2
B 4
C 12
D 18
▶️Answer/Explanation
Ans:A

