AP Calculus AB: 1.5 Determining Limits Using Algebraic Properties of Limits

AP PhysicsAP Calculus AP ChemistryAP Biology

Question

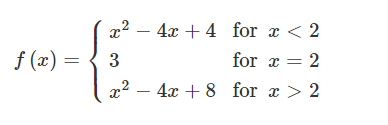
Let $f$ be the piecewise function defined above. The value of $\lim_{x\rightarrow 2^{+}}f(x)$ is

A 0

B 3

C 4

D non existent

▶️Answer/Explanation

Ans:C

$\lim_{x\rightarrow 2^{+}}f(x)=\lim_{x\rightarrow 2^{+}}x^{2}-4x+8=4-2.2+8=4$

Question

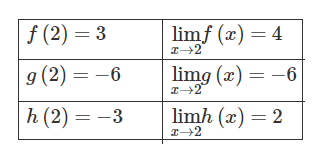
The table above gives selected values and limits of the functions $f$

$f$

, $g$ , and $h$ . What is $\lim_{x \to 2} (h (x) (5 f (x) + g (x)))$ ?

A -27

B-20

C 28

D 34

▶️Answer/Explanation

Ans: C

$\lim_{x\rightarrow 2}(h(x)(5f(x)+g(x)))=\lim_{x\rightarrow 2}h(x).(5\lim_{x\rightarrow 2}f(x)+\lim_{x\rightarrow 2}g(x))=2.(5.4-6)=$ 28

Question

$\lim_{x\rightarrow -3}\frac{x^{2}-9}{x^{2}-2x-15}$

A 0

B $\frac{3}{5}$

C$\frac{3}{4}$

D 1

E non existent

▶️Answer/Explanation

Ans:C

Question

If $f$ is the function defined by then $f(x)=\frac{x^{2}-4}{x^{2}+x-6}$ ,then $\lim_{x\rightarrow 2}f(x)$ is:

A 0

B $\frac{2}{3}$

C $\frac{4}{5}$

D non existent

▶️Answer/Explanation

Ans:C

$f(x)=\frac{x^{2}-4}{x^{2}+x-6}=\frac{(x-2)(x+2)}{(x+3)(x-2)}=\frac{(x+2)}{(x+3)}$ for x close to ,but not equal to ,2.Therefore, $\lim_{x\rightarrow 2}f(x)=\lim_{x\rightarrow 2}\frac{x+2}{x+3}=\frac{2+2}{2+3}=\frac{4}{5}$

Question

$\lim_{x\rightarrow -4}\frac{x+4}{x^{3}-16x}$ is

A 0

B $\frac{1}{32}$

C 1

D non existent

▶️Answer/Explanation

Ans:B

To evaluate this limit, it is helpful to first rearrange the expression into an equivalent form by factoring and dividing common factors.

$\lim_{x\rightarrow -4}\frac{x+4}{x^{3}-16x}=\lim_{x\rightarrow -4}\frac{x+4}{x(x-4)(x+4)}=\lim_{x\rightarrow -4}\frac{1}{x(x-4)}=\frac{1}{-4(-4-4)}$ $=\frac{1}{32}$

AP Calculus AB: 1.5 Determining Limits Using Algebraic Properties of Limits – Exam Style questions with Answer- MCQ

Question

Question

Question

Question

Question

Resources

Members

Company