Question:
The function f is defined by \(f(x)=\sqrt{25-x^{2}}\) for -5 ≤ x ≤ 5.
(a) Find f'(x).
(b) Write an equation for the line tangent to the graph of f at x = -3.
(c) Let g be the function defined by \(g(x)=\left\{\begin{matrix}
f(x) &for -5\leq x\leq -3 & & \\x+7
&for -3<x\leq 5. & &
\end{matrix}\right.\)
Is g continuous at x = -3 ? Use the definition of continuity to explain your answer
(d) Find the value of \(\int_{0}^{5}x\sqrt{25-x^{2}}dx.\)
▶️Answer/Explanation
Ans:
(a)
\(= (25-x^{2})^{1/2}\)
\(f'(x)=\frac{1.-2x}{2\sqrt{25-x^{2}}}=\frac{-x}{\sqrt{25-x^{2}}}\)
(b)
\(f'(-3)=\frac{3}{\sqrt{25-9}}=\frac{3}{\sqrt{16}}=\frac{3}{4}\) \(f(-3)=\sqrt{25-9}= \sqrt{16}=4\)
\(y = \frac{3}{4}(x+3)+4\)
(c)
\(\lim_{x\rightarrow -3^{-}}g(x)=f(-3)=4\) therefore \(\lim_{x\rightarrow -3}g(x)=4\)
\(\lim_{x\rightarrow -3^{+}}g(x)=-3+7=4\)
g(-3) = f(-3) = 4 \(\lim_{x\rightarrow -3}g(x)\) exists and is equal to g(-3)
g is continuous at x = -3
(d)
u = 25-x2 \(\frac{-1}{2}\int_{25}^{0}4^{1/2}du = \frac{1}{2}\int_{0}^{25}4^{1/2}du = \frac{1}{2}.\frac{24}{3}^{3/2}\int_{0}^{25}\)
\(\frac{-1}{2}du = +2xdx\)
\(= \frac{1}{3}.25^{3/2}=\frac{125}{3}\)
Question:
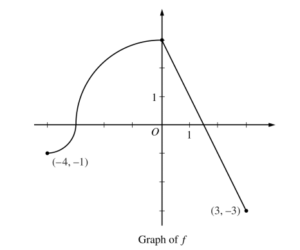
The continuous function f is defined on the interval -4 ≤ x ≤ 3. The graph of f consists of two quarter circles and one line segment, as shown in the figure above. Let \(g(x)=2x+\int_0^x f(t)dt\).
(a) Find g(-3) . Find g'(x) and evaluate g'(-3) .
(b) Determine the x-coordinate of the point at which g has an absolute maximum on the interval -4 ≤ x ≤ 3. Justify your answer.
(c) Find all values of x on the interval -4 ≤ x ≤ 3 for which the graph of g has a point of inflection. Give a reason for your answer.
(d) Find the average rate of change of f on the interval-4 ≤ x ≤ 3. There is no point c, -4 < c < 3, for which f'(c) is equal to that average rate of change. Explain why this statement does not contradict the Mean Value Theorem.
▶️Answer/Explanation
Ans:
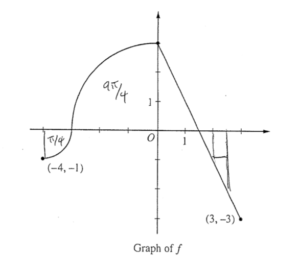
(a)
\(g(-3)=2(-3)+\int_{0}^{-3}f(t)dt = -6 -\frac{9\pi }{4}\)
\(g'(x)=\frac{d}{dx}\left ( 2x + \int_{0}^{x}f(t)dt \right )=2+f(x)\)
g'(-3) = 2 + f(-3) = 2 + 0 = 2
(b)
g'(x) = 0 2 + f(x) = 0
g'(x) f(x) = -2
x = 5/2
\(g(-4)=-8+\int_{0}^{-4}f(t)dt\)
= -8 – 2π
\(g(5/2)= 5+\int^{\frac{5}{2}}_{0} f(t)dt = + \frac{5}{4}\)
\(g(3)= 6+\int_{0}^{3}f(t)dt = 6\)
x = 5/2 , because g’ going from t to – proves it as the only relative maximum and g(5/2) is greater than g at either endpoint.
(c)
f'(x) g”(x) = d/dx (g(x)) = f'(x)
The only point of inflection for g is at x = 0, since f'(x), which is equivalent to g”, only changes signs at x = 0 on the interval -4 ≤ x ≤ 3
(d)
Avg. Rate of change = \(\frac{f(3)-f(-4)}{3-4}\)
\(\frac{-3-1}{3+4}=\frac{-2}{7}\)
Because mean value Theorem only applies when the function is continuous And differentiable on the interval, which doesn’t apply here since f(x) isn’t differentiable at x = 0.
Question:
| t (hours) | 0 | 1 | 3 | 6 | 8 |
| R (t) (liters / hour) | 1340 | 1190 | 950 | 740 | 700 |
Water is pumped into a tank at a rate modeled by \(W(t)= 2000e^{-t^{2}/20}\) liters per hour for 0 ≤ t ≤ 8, where t is measured in hours. Water is removed from the tank at a rate modeled by R (t) liters per hour, where R is differentiable and decreasing on 0 ≤ t ≤ 8. Selected values of R (t) are shown in the table above. At time t 0, there are 50,000 liters of water in the tank.
(a) Estimate R'(2). Show the work that leads to your answer. Indicate units of measure.
(b) Use a left Riemann sum with the four subintervals indicated by the table to estimate the total amount of water removed from the tank during the 8 hours. Is this an overestimate or an underestimate of the total amount of water removed? Give a reason for your answer.
(c) Use your answer from part (b) to find an estimate of the total amount of water in the tank, to the nearest liter, at the end of 8 hours.
(d) For 0 ≤ t ≤ 8, is there a time t when the rate at which water is pumped into the tank is the same as the rate at which water is removed from the tank? Explain why or why not.
▶️Answer/Explanation
Ans:
(a)
\(R'(2)\approx \frac{R(3)-R(1)}{3-1}=\frac{950-1190}{2}\)
R'(2) ≈ -120 L/hr2
(b)
\(\int_{0}^{8}R(t)dt\approx L_{4}=(1)(1340)+(2)(1190)+(3)(950)+(2)(740)\)
\(\int_{0}^{8}R(t)dt\approx 8,050 L\)
This is an underestimate because we are taking the left Riemann sum of a decreasing function. Therefore the left endpoints are greater than the right endpoints in each subinterval.
(c)
t = + 50, 000 L
Total left ≈ 50,000 + \(\left ( \int_{0}^{8}W(t)dt – \int_{0}^{8}R(t)dt \right )\)
\(\int_{0}^{8}W(t)dt = 7836.19532455\)
Total left ≈ 50,000 + (7836.19332455-8050)
Total left ≈ 49,786 L
(d)
T(t) = W(t) – R(t)
T(0) = 2000 – 1340 = 600 -648.47 < 0 < 600
T(8) = 81.524-700 = -618.47
When T(t) = 0, the rate of water being pumped in to the tank is equal to the rate of water being pumped out. Because the function T(t) is continuous and differentiable by IVT these exists some t on the interval [0, 8] where T(t) = 0.
Question
The temperature, in degrees Celsius \((^{\circ}C) \), of an oven being heated is modeled by an increasing differentiable function H of time t, where t is measured in minutes. The table above gives the temperature as recorded every 4 minutes over a 16-minute period.
(a) Use the data in the table to estimate the instantaneous rate at which the temperature of the oven is changing at time t = 10. Show the computations that lead to your answer. Indicate units of measure.
(b) Write an integral expression in terms of H for the average temperature of the oven between time t =0 and time t = 16. Estimate the average temperature of the oven using a left Riemann sum with four subintervals of equal length. Show the computations that lead to your answer.
(c) Is your approximation in part (b) an underestimate or an overestimate of the average temperature? Give a reason for your answer.
▶️Answer/Explanation
(d) Are the data in the table consistent with or do they contradict the claim that the temperature of the oven is increasing at an increasing rate? Give a reason for your answer.
(a)\(H’=\frac{H(12)-H(8)}{12-8}\)=\(\frac{80-73}{4}\)=\(\frac{7}{4}^{\circ}C/min\)
(b)Average temperature is \(\frac{1}{16}H(t)dt\)
\(\int_{0}^{16}H(t)dt\simeq 4.(65+68+73+80)\)
Average temperature\( \simeq \frac{4.286}{16}=71.5^{\circ}C\)
(c) The left Riemann sum approximation is an underestimate of the integral because the graph of H is increasing. Dividing by 16 will not change the inequality, so 71.5°C is an underestimate of the average temperature.
(d) If a continuous function is increasing at an increasing rate, then the slopes of the secant lines of the graph of the function are increasing. The slopes of the secant lines for the four intervals in the table are \(\frac{3}{4}\), \(\frac{5}{4}\),\(\frac{7}{4}\)and\( \frac{10}{4}\), respectively. Since the slopes are increasing, the data are consistent with the claim. OR By the Mean Value Theorem, the slopes are also the values of \(H'(c_{k})\) for some times \(c_1 < C_2 < C_3 < C_4\), respectively. Since these derivative values are positive and increasing, the data are consistent with the claim.
