Question
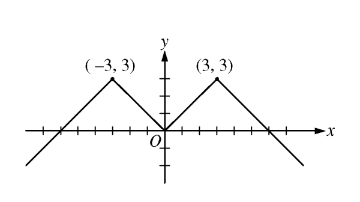
The graph of the even function y = f’ ( x) consists of 4 line segments, as shown above. Which of the following statements about f is false?
(A) \(\lim_{x\rightarrow 0}(f(x)-f(0))=0\)
(B) \(\lim_{x\rightarrow 0}\frac{f(x)-f(-x)}{x}=0\)
(C) \(\lim_{x\rightarrow 0} \frac{f(x)-f(-x)}{2x}=0\)
(D)\(\lim_{x\rightarrow 2}\frac{f(x)-f(2)}{x-2}=1\)
(E) \(\lim_{x\rightarrow 3}\frac{f(x)-f(3)}{x-3} \)does not exist.
▶️Answer/Explanation
Ans:B
Question
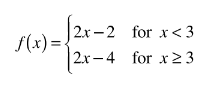
Let f be the piecewise-linear function defined above. Which of the following statements are true?
I. \(\lim_{h\rightarrow 0^{-}}\frac{f(3+h)-f(3)}{h}=2\)
II. \(\lim_{h\rightarrow 0^{+}}\frac{f(3+h)-f(3)}{h}=2\)
III. \(f'(3)=2\)
(A) None
(B) II only
(C) I and II only
(D) I, II, and III
▶️Answer/Explanation
Ans:B
Question
The derivative of a function f is given by \(f'(x)=0.2x+e^{0.15x}\). Which of the following procedures can be used to determine the value of x at which the line tangent to the graph of f has slope 2 ?
A Evaluate \(0.2x+e^{0.15x}\) at x=2.
B Evaluate \(\frac{\mathrm{d} }{\mathrm{d} x}(0.2x+e^{0.15x})\) at x=2.
C Solve \(0.2x+e^{0.15x}\) for x.
D Solve \(\frac{\mathrm{d} }{\mathrm{d} x}(0.2x+e^{0.15x})=2\) for x.
▶️Answer/Explanation
Ans:C
Since the derivative at a point is the slope of the line tangent to the graph at that point, solving \(f{}'(x)=0.2x+e^{0.15x}=2\) will yield the value of x at which the line tangent to the graph of f has slope 2.
Question
The derivative of the function f is given by f′(x)=−2x+4 for all x, and f(−1)=5. Which of the following is an equation for the line tangent to the graph of f at x=−1 ?
A y=−2x+3
B y=−2x+4
C y=6x+5
D y=6x+11
▶️Answer/Explanation
Ans:D
The slope of the line tangent to the graph of f at x=−1 is f′(−1)=−2(−1)+4=2+4=6. An equation for the line containing the point (−1,5) with slope 6 is y=6(x+1)+5=6x+11.
