Question
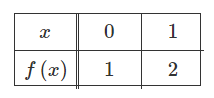
Let f be the function given by \(f(x)=2^{x^{2}}\) . Selected values of f are given in the table above. If the values in the table are used to approximate f′(0.5), what is the difference between the approximation and the actual value of f′(0.5) ?
A 0
B 0.176
C 0.824
D 1
▶️Answer/Explanation
Ans:B
The numerical value of the derivative at x=0.5 obtained from the calculator is f′(0.5)=0.824. A difference quotient can be used with the values in the table to estimate the derivative as \(\frac{f(1)-f(0)}{1-0}=\frac{2-1}{1}=1\). The error between the actual derivative value and this approximation is 0.176.
Question
Let f be the function given by \(f(x)=\frac{1}{7}x^{7}-\frac{7}{6}x^{6}+3x^{5}-\frac{5}{4}x^{4}-\frac{16}{3}x^{3}+6x^{2}\). Which of the following statements is true?
A f′(−1.1)<f′(0.5)<f′(1.4)
B f′(−1.1)<f′(1.4)<f′(0.5)
C f′(0.5)<f′(1.4)<f′(−1.1)
D f′(1.4)<f′(0.5)<f′(−1.1)
▶️Answer/Explanation
Ans:D
The calculator is used to store the expression for f(x) and to find the numerical derivative values at the three values of x. They are, in increasing order, f′(1.4)=−0.774, f′(0.5)=2.109, and f′(−1.1)=9.102.
Question

The graph of the trigonometric function f is shown above for a≤x≤b. At which of the following points on the graph of f could the instantaneous rate of change of f equal the average rate of change of f on the interval [a,b] ?
A A
B B
C C
D D
▶️Answer/Explanation
Ans:B
The instantaneous rate of change of f at the point B is the slope of the line tangent to the graph of f at the point B. The average rate of change of f on the interval [a,b] is the slope of the secant line through the points (a,f(a)) and (b,f(b)). The tangent line at B appears to be parallel to the secant line. Therefore, the instantaneous rate of change at B could be equal to the average rate of change.
Question
If \( f(x)=2+|x-3|\)for all x, then the value of the derivative f ′(x ) at x = 3 is.
(A) -1 (B) 0 (C) 1 (D) 2 (E) nonexistent
▶️Answer/Explanation
Ans:E
E There is no derivative at the vertex which is located at x = 3.
Question
The point on the curve \(x^{2}+2y=0\) that is nearest the point \( \left ( 0,-\frac{1}{2} \right )\) occurs where y is
(A) \( \frac{1}{2}\) (B) 0 (C)\( -\frac{1}{2}\) (D) −1 (E) none of the above
▶️Answer/Explanation
Ans:B

