Question:

The function f is defined on the closed interval [-5, 4] . The graph of f consists of three line segments and is shown in the figure above. Let g be the function defined by \(g(x)=\int_{-3}^{x}f(t)dt.\)
(a) Find g(3) .
(b) On what open intervals contained in -5 < x < 4 is the graph of g both increasing and concave down? Give a reason for your answer.
(c) The function h is defined by \(h(x)= \frac{g(x)}{5x}\). Find h'(3).
(d) The function p is defined by p(x) = f(x2 – x). Find the slope of the line tangent to the graph of p at the point where x = -1.
▶️Answer/Explanation
Ans:
\(g(x)= \int_{-3}^{3}f(t)dt\)
\(= \frac{1}{2}(5)(4)-\frac{1}{2}(1)(2)\)
= 10 – 1 = 9
(b)
g'(x) > 0 ⇔ f(x) > 0
g”(x) < 0 ⇔ f'(x) < 0
(-5, -3), (0, 2)
(c)
\(h(x)=\frac{g(x)}{5x}\)
\(h'(x)= \frac{(5x)(g'(x))-g(x).5}{25x^{2}}\)
\(h'(3)= \frac{(15)(f(3))-g(3).5}{9.25}=\frac{(15)(-2)-(9)(5)}{9.25}\)
(d)
p(x) = f(x2 – x)
p'(x) = f'(x2-x) . (2x-1)
p'(-1) = f'(1+1) . (-2-1) = f'(2).-3
= (-2) (-3)
= 6
\({f}'(2)=\frac{-4-4}{4-0}=\frac{-8}{4}=-2\)
Question
Consider the family of functions \(f(x)=\frac{1}{x^{2}-2x+k},\) where k is a constant.
(a) Find the value of k, for k > 0, such that the slope of the line tangent to the graph of f at x = 0 equals 6.
(b) For k = −8, find the value of \(\int_{0}^{1}f(x)dx.\)
(c) For k = 1, find the value of \(\int_{0}^{1}f(x)dx\) or show that it diverges.
▶️Answer/Explanation
Ans:
(a) \(f'(x)=\frac{-(2x-2)}{\left ( x^{2}-2x+k \right )^{2}}\)
\(f'(0)=\frac{2}{k^{2}}=6\Rightarrow k^{2}=\frac{1}{3}\Rightarrow k = \frac{1}{\sqrt{3}}\)
(b) \(\frac{1}{x^{2}-2x-8}=\frac{1}{(x-4)(x+2)}=\frac{A}{x-4}+\frac{B}{x+2}\)
\(\Rightarrow 1 = A(x+2)+B(x-4)\)
\(\Rightarrow A = \frac{1}{6}, B=-\frac{1}{6}\)
\(\int_{0}^{1}f(x)dx=\int_{0}^{1}\left ( \frac{\frac{1}{6}}{x-4} -\frac{\frac{1}{6}}{x+2}\right )dx\)
\(=\left [\frac{1}{6}In|x-4| -\frac{1}{6} In|x+2| \right ]_{x=0}^{x=1}\)
\(=\left ( \frac{1}{6}In3-\frac{1}{6}In3 \right )-\left ( \frac{1}{6}In4-\frac{1}{6}In2 \right )=-\frac{1}{6}In2\)
(c) \(\int_{0}^{2}\frac{1}{x^{2}-2x+1}dx=\int_{0}^{2}\frac{1}{(x-1)^{2}}dx=\int_{0}^{1}\frac{1}{(x-1)^{2}}dx+\int_{1}^{2}\frac{1}{(x-1)^{2}}dx\)
\(=\lim_{b\rightarrow 1^{-}}\int_{0}^{b}\frac{1}{(x-1)^{2}}dx+\lim_{b\rightarrow 1^{+}}\int_{b}^{2}\frac{1}{(x-1)^{2}}dx\)
\(=\lim_{b\rightarrow 1^{-}}\left ( -\frac{1}{x-1|_{x=0}^{x=b}} \right )+\lim_{b\rightarrow 1^{+}}\left ( -\frac{1}{x-1|_{x=b}^{x=2}} \right )\)
\(=\lim_{b\rightarrow 1^{-}}\left ( -\frac{1}{b-1}-1 \right )+\lim_{b\rightarrow 1^{+}}\left ( -1+\frac{1}{b-1} \right )\)
Because \(=\lim_{b\rightarrow 1^{-}}\left ( -\frac{1}{b-1} \right )\) does not exist, the integral diverges.
Question:
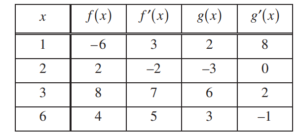
The functions f and g have continuous second derivatives. The table above gives values of the functions and their derivatives at selected values of x.
(a) Let k(x) = f(g(x)). Write an equation for the line tangent to the graph of k at x = 3.
(b) Let \(h(x)=\frac{g(x)}{f(x)}.\) Find h'(1).
(c) Evaluate \(\int_{1}^{3}f”(2x)dx.\)
▶️Answer/Explanation
Ans:
(a)
K(3) = f(g(3))
= f(6)
= 4
k'(x) = f'(g(x)) ·g'(x)
k'(3) = f'(g(3))·g'(3)
= f'(6)·2
= 5.2
= 10
y – 4 = 10 (x-3)
(b)
\(h'(x)=\frac{f(x)g'(x)-g(x)f'(x)}{(f(x))^{2}}\) \(h'(1)=\frac{-2}{2}\)
\(h'(1)=\frac{f(1)g'(1)-g(1)f'(1)}{(f(1))^{2}}\)
\(=\frac{(-6)(8)-(2)(3)}{(-6)^{2}}\)
\(=\frac{-48-6}{36}\)
\(=\frac{-54}{36}\)
(c)
\(\left [ \frac{1}{2}f'(2x) \right ]_{1}^{3}\)
\(\left [ \frac{1}{2}f'(6) \right ]-\left [ \frac{1}{2}f'(2) \right ]\)
\(\frac{5}{2}+1\)
\(\frac{7}{2}\)
Question:
| t (years) | 2 | 3 | 5 | 7 | 10 |
| H(t) (meters) | 1.5 | 2 | 6 | 11 | 15 |
The height of a tree at time t is given by a twice-differentiable function H, where H (t) is measured in meters and t is measured in years. Selected values of H (t) are given in the table above.
(a) Use the data in the table to estimate H'(6). Using correct units, interpret the meaning of H'(6) in the context of the problem.
(b) Explain why there must be at least one time t, for 2 < t <10 , such that H'(t) = 2.
(c) Use a trapezoidal sum with the four subintervals indicated by the data in the table to approximate the average height of the tree over the time interval 2 ≤ t ≤ 10 .
(d) The height of the tree, in meters, can also be modeled by the function G, given by \(G(x)=\frac{100x}{1+x}\) , where x is the diameter of the base of the tree, in meters. When the tree is 50 meters tall, the diameter of the base of the tree is increasing at a rate of 0.03 meter per year. According to this model, what is the rate of change of the height of the tree with respect to time, in meters per year, at the time when the tree is 50 meters tall?
▶️Answer/Explanation
Ans:
(a)
\(H'(6)\approx \frac{\Delta H(t)}{\Delta t}\approx \frac{H(7)-H(5)/m}{(7-5)_{y}}=\frac{(11-6)m}{(7-5)y}=\frac{5 meters}{2 years}\)
When t = 6 years, the rate of which the tree is growing is H'(6) meters per year
(b)
By the MVT, as H(t) is continuous and differentiable on t ∈ (2, 10), there must be H'(c) = 2 where 2 < c < 10 if there exists \(\frac{H(b)-H(a)}{b-a}=2\) on the interval (2, 10). \(\frac{H(5)-H(3)}{(5-3)_{years}}=\frac{6m-2m}{2years}=2 m/y\) So c exists on interval c ∈ (2, 10)
(c)
Total height : \(\frac{1}{2}\left ( 1(1.5+2)+2(2+6)+2(6+11)+3(11+15) \right )\)
Average height : \(\frac{1}{10_{y}-2_{yr}} Total ht = \frac{1}{8}\times \frac{1}{2}\left ( 3.5 + 2(8)+2(17)+3(26) \right ) meters\)
(d)
\(G(x)=\frac{100x}{1+x}\) G(x) = 50 \(\frac{dx}{dt}=0.03 m/y\)
\(G'(x)=\frac{100\frac{dx}{dt}(1+x)-\left ( \frac{dx}{dt} \right )100x}{(1+x)^{2}}\) \(\frac{100\times 0.03(2)-0.03\times 100}{4}\)
\(50 = \frac{100x}{1+x}\Rightarrow 50(1+x)=100x\) \(\frac{6-3}{4}=\frac{3}{4}m/year\)
⇒ 1 = x x = 1m
Question
| x | f(x) | f'(x) | g(x) | g'(x) |
| 1 | -6 | 3 | 2 | 8 |
| 2 | 2 | -2 | -3 | 0 |
| 3 | 8 | 7 | 6 | 2 |
| 6 | 4 | 5 | 3 | -1 |
The functions f and g have continuous second derivatives. The table above gives values of the functions and their derivatives at selected values of x.
(a) Let k(x) = f(g(x)). Write an equation for the line tangent to the graph of k at x = 3.
(b) Let \(h(x)=\frac{g(x)}{f(x)}.\) Find h'(1).
(c) Evaluate \(\int_{1}^{3}f”(2x)dx.\)
▶️Answer/Explanation
Ans:
(a) k(3) = f(g(3)) = f(6) = 4
k'(3) = f'(g(3))·g'(3) = f'(6)·2=5·2 =10
An equation for the tangent line is y = 10(x -3) +4.
(b) \(h'(1)=\frac{f(1)\cdot g'(1)-g(1)\cdot f'(1)}{(f(1))^{2}}\)
\(=\frac{(6)\cdot 8-2\cdot 3}{(-6)^{2}}=\frac{-54}{36}=-\frac{3}{2}\)
(c) \(\int_{1}^{3}f”(2x)dx=\frac{1}{2}\left [ f'(2x) \right ]_{1}^{3}=\frac{1}{2}\left [ f'(6)-f'(2) \right ]\)
\(=\frac{1}{2}\left [ 5-(-2) \right ]=\frac{7}{2}\)
Question
Consider the function \(f(x)=\frac{1}{x^{2}-kx},\) where k is a nonzero constant. The derivative of f is given by \(f'(x)=\frac{k-2x}{\left ( x^{2}-kx \right )^{2}}.\)
(a) Let k = 3, so that \(f(x)=\frac{1}{x^{2}-3x}.\) Write an equation for the line tangent to the graph of f at the point whose x-coordinate is 4.
(b) Let k = 4, so that \(f(x)=\frac{1}{x^{2}-4x}.\) Determine whether f has a relative minimum, a relative maximum, or neither at x = 2. Justify your answer.
(c) Find the value of k for which f has a critical point at x = -5.
(d) Let k = 6, so that \(f(x)=\frac{1}{x^{2}-6x}\) Find the partial fraction decomposition for the function f. Find \(\int f(x)dx.\)
▶️Answer/Explanation
Ans:
(a) \(f(4)=\frac{1}{4^{2}-3\cdot 4}=\frac{1}{4}\) \(f'(4)=\frac{3-2\cdot 4}{\left ( 4^{2}-3\cdot 4 \right )^{2}}=-\frac{5}{16}\)
An equation for the line tangent to the graph of f at the point whose x-coordinate is 4 is \(y= -\frac{5}{16}(x-4)+\frac{1}{4}.\)
(b) \(f'(x)=\frac{4-2x}{\left ( x^{2}-4x \right )^{2}}\) \(f'(2)=\frac{4-2\cdot 2}{\left ( 2^{2}-4\cdot 2 \right )^{2}}=0\)
f'(x) changes sign from positive to negative at x = 2. Therefore, f has a relative maximum at x = 2.
(c) \(f'(-5)=\frac{k-2\cdot (5)}{\left ( (-5)^{2}-k\cdot (-5) \right )^{2}}=0\Rightarrow k = -10\)
(d) \(\frac{1}{x^{2}-6x}=\frac{1}{x(x-6)}=\frac{A}{x}+\frac{B}{x-6}\Rightarrow 1=A(x-6)+Bx\)
\(x = 0 \Rightarrow 1 = A\cdot (-6)\Rightarrow A = -\frac{1}{6}\)
\(x = 6 \Rightarrow 1 = B\cdot (6)\Rightarrow B = \frac{1}{6}\)
\(\frac{1}{x(c-6)}=\frac{-1/6}{x}+\frac{1/6}{x-6}\)
\(\int f(x)dx-\int \left ( \frac{-1/6}{x}+\frac{1/6}{x-6} \right )dx\)
\(=-\frac{1}{6}In|x| +\frac{1}{6}In|x-6|+C=\frac{1}{6}In\left | \frac{x-6}{x} \right |+C\)
Question
Let f be the function given by \(f(x)=\frac{\sin ^{2}(x)}{x}\).
(A) Find the derivative of f (x).
(B) Write an equation for the tangent line at \(x=\frac{\pi }{2}\).
▶️Answer/Explanation
(A)\(f'(x)=\frac{2x\sin x\cos x-\sin ^{2}x}{x^{2}}=\frac{\sin x(2x\cos x-\sin x)}{x^{2}}\)
(B) At \(x=\frac{\pi }{2},f\left ( \frac{\pi }{2} \right )=\frac{2}{\pi }\),while\( f’\left ( \frac{\pi }{2} \right )=-\frac{4}{\pi ^{2}}\).Using the point-slope formula:\(y-\frac{2 }{\pi }=-\frac{4}{\pi ^{2}}\left ( x-\frac{\pi }{2} \right ) y=-\frac{4}{\pi ^{2}}x+\frac{4}{\pi }\)
