Home / AP Calculus AB: 3.3 Differentiating Inverse Functions – Exam Style questions with Answer- MCQ

AP Calculus AB: 3.3 Differentiating Inverse Functions – Exam Style questions with Answer- MCQ

AP Calculus AB-Questions and Answers - All Topics

Question

Let \( f \) and \( g \) be inverse functions that are differentiable for all \( x \). If \( f(3) = -2 \) and \( g'(-2) = -4 \), which of the following statements must be false?

I. \( f'(0) = \frac{1}{4} \)
II. \( f'(3) = -\frac{1}{4} \)
III. \( f'(5) = -\frac{1}{4} \)

A) I only
B) II only
C) III only
D) I and III only

▶️ Answer/Explanation

Solution

Correct Answer: A

Step 1: Use the inverse function theorem:
\[ g'(f(a)) = \frac{1}{f'(a)} \]
Step 2: Substitute given values \( f(3) = -2 \) and \( g'(-2) = -4 \):
\[ g'(-2) = \frac{1}{f'(3)} \implies -4 = \frac{1}{f'(3)} \implies f'(3) = -\frac{1}{4} \]
Step 3: Analyze statements:

  • Statement II is true since \( f'(3) = -\frac{1}{4} \).
  • Statement I claims \( f'(0) = \frac{1}{4} \). However, \( f \) is strictly decreasing (since \( f'(3) < 0 \)), so \( f'(0) \) must also be negative. Thus, \( f'(0) = \frac{1}{4} \) is impossible.
  • Statement III is possible since \( f \) is decreasing, and \( f'(5) \) could be \( -\frac{1}{4} \).

Conclusion: Only Statement I must be false.

Question

Let \( f \) and \( g \) be functions that are differentiable everywhere. If \( g \) is the inverse function of \( f \) and if \( g(-2) = 5 \) and \( f'(5) = -\frac{1}{2} \), then \( g'(-2) = \) ?

A) 2
B) \(\frac{1}{2}\)
C) \(\frac{1}{5}\)
D) \(-\frac{1}{5}\)
E) -2

▶️ Answer/Explanation

Solution

Correct Answer: E

Step 1: Recall the inverse function theorem formula:
\[ g'(a) = \frac{1}{f'(g(a))} \]
Step 2: Substitute the given values \( g(-2) = 5 \) and \( f'(5) = -\frac{1}{2} \):
\[ g'(-2) = \frac{1}{f'(5)} = \frac{1}{-\frac{1}{2}} = -2 \]
Explanation:

  1. Since \( g \) is the inverse of \( f \), we apply the inverse function theorem.
  2. The point \( g(-2) = 5 \) tells us that \( f(5) = -2 \) by inverse function property.
  3. The derivative relationship gives \( g'(-2) \) directly from \( f'(5) \).

Question

The function \( f \) is increasing and differentiable. Selected values of \( f \) and its derivative \( f’ \) are given in the table above. What is the value of \( (f^{-1})'(3) \)?

A) \(\frac{1}{4}\)
B) \(\frac{1}{2}\)
C) 1
D) 2

▶️ Answer/Explanation

Solution

Correct Answer: A

Step 1: From the table, we see that \( f(2) = 3 \). Since \( f \) is increasing and differentiable, its inverse \( f^{-1} \) exists and is differentiable.

Step 2: Apply the inverse function theorem:
\[ (f^{-1})'(3) = \frac{1}{f'(f^{-1}(3))} \]
Step 3: From the table, \( f^{-1}(3) = 2 \) and \( f'(2) = 4 \):
\[ (f^{-1})'(3) = \frac{1}{f'(2)} = \frac{1}{4} \]
Explanation:

  1. Identify the point where \( f(x) = 3 \) from the table (x=2).
  2. Use the inverse function theorem formula.
  3. Substitute the derivative value from the table at x=2.

Function table

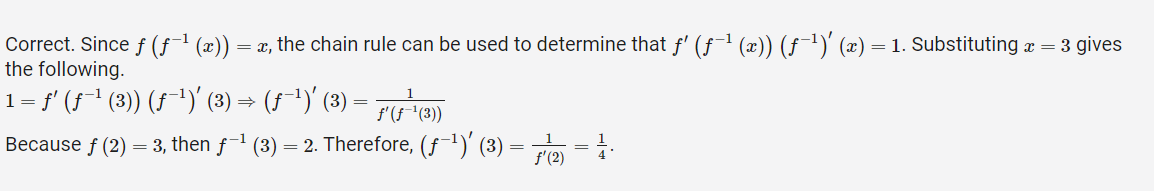
Question

Let \( f(x) = (2x + 1)^3 \) and let \( g \) be the inverse function of \( f \). Given that \( f(0) = 1 \), what is the value of \( g'(1) \)?

A) \(-\frac{2}{27}\)
B) \(\frac{1}{54}\)
C) \(\frac{1}{27}\)
D) \(\frac{1}{6}\)
E) 6

▶️ Answer/Explanation

Solution

Correct Answer: D

Step 1: Find the derivative of \( f(x) \):
\[ f'(x) = 3(2x + 1)^2 \times 2 = 6(2x + 1)^2 \]
Step 2: Since \( g \) is the inverse of \( f \), we know \( g(1) = 0 \) because \( f(0) = 1 \).
Step 3: Apply the inverse function theorem:
\[ g'(1) = \frac{1}{f'(g(1))} = \frac{1}{f'(0)} \]
Step 4: Calculate \( f'(0) \):
\[ f'(0) = 6(2(0) + 1)^2 = 6(1)^2 = 6 \]
Step 5: Compute \( g'(1) \):
\[ g'(1) = \frac{1}{6} \]
Explanation:

  1. Differentiate the original function using the chain rule.
  2. Use the given \( f(0) = 1 \) to find \( g(1) = 0 \).
  3. Apply the inverse function theorem formula.
  4. Evaluate the derivative at the appropriate point.
More AP Calculus AB MCQ Questions..
Scroll to Top