Question
\(\frac{d}{dx}\left ( 2^{x} \right )\)=
(A)\(2^{x-1}\) (B)\((2^{x-1})\) (C)\((2^{x})ln2\) (D)\((2^{x-1})ln2\) (E)\(\frac{2x}{ln2}\)
▶️Answer/Explanation
Ans:C
\(\frac{d}{dx}(2^{x})=2^{x}.ln2\)
Question
\(f(x)=ln\left | x^2-1 \right |\), then \({f}'(x)\)
(A)\(\left | \frac{2x}{x^2-1} \right |\)
(B)\(\frac{2x}{|x^2-1|}\)
(C)\(\frac{2|x|}{x^2-1}\)
(D)\(\frac{2x}{x^2-1}\)
(E)\(\frac{1}{x^2-1}\)
▶️Answer/Explanation
Ans:D
\(f(x)=ln|x^2-1|;f'(x)=\frac{1}{x^2-1}.\frac{d}{dx}(x^2-1)=\frac{2x}{x^2-1}\)
Question
\(\frac{d}{dx}\left ( x^{lnx} \right )\)=
(A)\(x^{lnx}\) (B)\((lnx)^{x}\) (C)\(\frac{2}{x}(lnx)x^{lnx}\) (D)\( (lnx) \left ( x^{lnx-1} \right )\) (E)\(2(lnx)\left ( x^{lnx} \right )\)
▶️Answer/Explanation
Ans:C
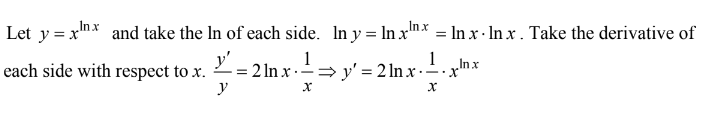
Question
Which of the following expressions can be differentiated using the product rule?
A. \(arcsin(cosx)\)
B. \(sinx(arccosx)\)
C. \(e^x+arctanx\)
D. \((12x^2+3x−6)^e\)
▶️Answer/Explanation
Ans:B
This expression is the product of \(sinx\) and \(arccosx\). Therefore, differentiation of the expression requires the use of the product rule.
