Question:
| t(hours) | 0 | 0.3 | 1.7 | 2.8 | 4 |
| \(v_P(t)\) (meters per hour) | 0 | 55 | -29 | 55 | 48 |
The velocity of a particle, P, moving along the x-axis is given by the differentiable function vp , where \(v_P(t)\) is measured in meters per hour and t is measured in hours. Selected values of \(v_P(t)\) are shown in the table above. Particle P is at the origin at time t = 0.
(a) Justify why there must be at least one time t, for 0.3 ≤ t ≤ 2.8, at which \(v_P(t)\) , the acceleration of particle P, equals 0 meters per hour per hour.
(b) Use a trapezoidal sum with the three sub-intervals [0, 0.3], [0.3, 1.7], and [1.7, 2.8] to approximate the value of \(\int_{0}^{2.8}v_{p}(t)dt.\)
(c) A second particle, Q, also moves along the x-axis so that its velocity for 0 ≤ t ≤ 4 is given by \(v_{Q}(t)=45\sqrt{t}cos(0.063t^{2})\) meters per hour. Find the time interval during which the velocity of particle Q is at least 60 meters per hour. Find the distance traveled by particle Q during the interval when the velocity of particle Q is at least 60 meters per hour.
(d) At time t = 0, particle Q is at position x = −90. Using the result from part (b) and the function vQ from part (c), approximate the distance between particles P and Q at time t = 2.8.
▶️Answer/Explanation
Ans:
(a)
\({v_{p}}'(t)=9_{p}(t)\) \(\frac{v_{p}(2.8)-v_{p}(0.3)}{2.8-0.3}\)
Since \(v_P(t)\) is a continuous and differentiable function, MVT states that there must be at least one time t, for 0.3 ≤ t ≤ 2.8 at which \({v_{p}}'(t)=\frac{v_{p}(2.8)-v_{p}(0.3)}{2.8-0.3}=\frac{55-55}{2.5}=0.\)
(b)
\(0.3\left ( \frac{55+0}{2} \right )+1.4\left ( \frac{-29+55}{2} \right )+1.1\left ( \frac{55+(-29)}{2} \right )\)
8.25 + 18.2 + 14.3
\(\int_{0}^{2.8}{v_{p}}^{(t)}=40.75\)
(c)
\(60 = 45\sqrt{t}cos (0.053t^{2})\)
t = 1.866, 3.519
1.866 ≤ t ≤ 3.519
\(\int_{1.866}^{3.519}45\sqrt{t}cos (0.063t^{2})dt\)
= 106.109
106.109 meters
(d)
\(X_p(2.8)= 40.75\)
\(x_{Q}(2.8) = -90 +\int_{0}^{2.8}45\sqrt{t}cos (0.063t^{2})dt\)
= -90 + 135.938 = 45.938
45.938 – 40.75 = 5.188
The distance between particles P and Q at t = 2.8 is 5.188 meters
Question:
A particle moves along the x-axis with velocity given by \(v(t)=\frac{10 sin(0.4t^{2})}{t^{2}-t+3}\) for time 0 ≤ t ≤ 3.5. The particle is at position x = −5 at time t = 0.
(a) Find the acceleration of the particle at time t = 3.
(b) Find the position of the particle at time t = 3.
(c) Evaluate \(\int_{0}^{3.5}v(t)dt,\) and evaluate \(\int_{0}^{3.5}|v(t)|dt.\) Interpret the meaning of each integral in the context of the problem.
(d) A second particle moves along the x-axis with position given by x2(t) = t2 − t for 0 ≤ t ≤ 3.5 . At what time t are the two particles moving with the same velocity?
▶️Answer/Explanation
Ans:
(a)
v'(3) = -2.1182
(b)
\(-5+\int_{0}^{3}v(t)dt=-1.7602\)
(c)
\(\int_{0}^{3.5}v(t)dt=2.8439,\) which is the displacement of the particle from t = 0 to t = 3.5
\(\int_{0}^{3.5}|v(t)|dt=3.7371,\) which is the total distance the particle traveled from t = 0 to t = 3.5
(d)
v(t) = 2t – 1
t = 1.5705
Question:
For 0 ≤ t ≤ 12, a particle moves along the x-axis. The velocity of the particle at time t is given by \(v(t)=cos(\frac{\pi }{6}t)\). The particle is at position x = -2 at time t = 0.
(a) For 0 ≤ t ≤ 12, when is the particle moving to the left?
(b) Write, but do not evaluate, an integral expression that gives the total distance traveled by the particle from time t = 0 to time t = 6.
(c) Find the acceleration of the particle at time t. Is the speed of the particle increasing, decreasing, or neither at time t = 4 ? Explain your reasoning.
(d) Find the position of the particle at time t = 4.
▶️Answer/Explanation
Ans:
x(0) = -2
(a)
\(cos (\frac{\pi }{6}t)=0\) when x = 3 , x = 9

The particle is moving left on (3, 9)
(b)
\(D = \int_{0}^{6}\left | cos(\frac{\pi }{6}t) \right |dt\)
(c)
\(a(t)=v'(t)=-sin(\frac{\pi }{6}t)\cdot \frac{\pi }{6}=-\frac{\pi }{6}sin(\frac{\pi }{6}t)\)
\(a(4)=-\frac{\pi }{6} sin (\frac{2\pi }{3})=-\frac{\pi }{6}\left ( \frac{\sqrt{3}}{2} \right )=\frac{-\pi \sqrt{3}}{12}\)
\(v(4)= cos \left ( \frac{2\pi }{3} \right )=\frac{-1}{2}\)
The speed is increasing because a(t) and v(t) have the same sign (-) at t = 4
(d)
\(u = \frac{\pi }{6}t\)
\(du = \frac{\pi }{6}dt\)
\(x(t)=\int cos(\frac{\pi }{6}t)dt\)
\(x(t)=\frac{\pi }{6}\int cos u du\)
\(x(t)=\frac{\pi }{6}sin(\frac{\pi }{6}t)+C\)
\(\frac{\pi }{6}sin(\frac{\pi }{6}t)+C = -2 \) when x = 0
\(\frac{\pi }{6}sin(0)+C = -2 \)
C = -2
\(x(t)=\frac{\pi }{6}sin(\frac{\pi }{6}t) -2 \)
\(x(4)=\frac{\pi }{6}sin(\frac{2\pi }{3}) -2 \)
\(x(4)=\frac{\pi }{6}\left ( \frac{\sqrt{3}}{2} \right ) -2 \)
\(x(4)=\frac{2\sqrt{3}}{\pi} -2 \)
Question:
| t (minutes) | 0 | 12 | 20 | 24 | 40 |
| v (t) (meters per minute) | 0 | 200 | 240 | -220 | 150 |
Johanna jogs along a straight path. For 0 ≤ t ≤ 40, Johanna’s velocity is given by a differentiable function v.
Selected values of v (t), where t is measured in minutes and v (t) is measured in meters per minute, are given in the table above.
(a) Use the data in the table to estimate the value of v'(16).
(b) Using correct units, explain the meaning of the definite integral \(\int_{0}^{40}|v(t)|dt\) in the context of the problem.
Approximate the value of \(\int_{0}^{40}|v(t)|dt\) using a right Riemann sum with the four subintervals indicated in the table.
(c) Bob is riding his bicycle along the same path. For 0 ≤ t ≤ 10, Bob’s velocity is modeled by B(t) = t3 – 6t + 300, where t is measured in minutes and B (t) is measured in meters per minute.
Find Bob’s acceleration at time t = 5.
(d) Based on the model B from part (c), find Bob’s average velocity during the interval0 ≤ t ≤ 10.
▶️Answer/Explanation
Ans:
(a)
\(V'(14)\approx \frac{v(20)-v(12)}{20-12}=\frac{240-200}{8}=\frac{40}{8}=\frac{20}{4}=5\frac{m}{min^{2}}\)
(b)
\(\int_{0}^{40}|v(t)|dt\) represents the total distance in meters Johanna traveled between times. t = 0 and t = 40 minutes.
\(\int_{0}^{40}|v(t)|dt\approx \left [ 12(200)+8(240)+4(220)+16(150) \right ]\)
= 2400 + 1920 + 880 + 2400
= 7600 meters
(c)
acceleration = B'(t) = 3t2 – 12t
B'(5) = 3(5)2 – 12(5)
= 75-60 = 15 \(\frac{m}{min^{2}}\)
(d)
Avg. Velocity = \(\frac{1}{10}\int_{0}^{10}(t^{3}-6t^{2}+300)dt\)
\(=\frac{1}{10}\cdot \left [ \frac{t^{4}}{4} -2t^{3}+300t\right ]_{0}^{10}\)
\(=\frac{1}{10}\cdot \left [ \frac{10000}{4} -2000+300t\right ]\)
\(=\frac{1}{10}\left [ 3500\right ]=350\frac{m}{min}\)
Question:
Two particles move along the x-axis. For 0 ≤ t ≤ 8, the position of particle P at time t is given by xp(t) = ln(t2 − 2t + 10 ) , while the velocity of particle Q at time t is given by vQ(t) = t2 − 8t + 15 . Particle Q is at position x = 5 at time t = 0.
(a) For 0 ≤ t ≤ 8, when is particle P moving to the left?
(b) For 0 ≤ t ≤ 8, find all times t during which the two particles travel in the same direction.
(c) Find the acceleration of particle Q at time t = 2. Is the speed of particle Q increasing, decreasing, or neither at time t = 2 ? Explain your reasoning.
(d) Find the position of particle Q the first time it changes direction.
▶️Answer/Explanation
Ans:
(a)
\({v_{p}}(t)\) is neg.
\({v_{p}}(t)= {x_{p}}'(t)=\frac{1}{t^{2}+2t+10}\cdot (2t-2)\)
\(0=\frac{2t-2}{t^{2}+2t+10}\)
2t – 2 = 0
t = 1
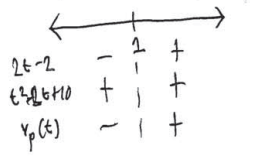
Particle p is moving to the left on 0 ≤ t < 1.
(b)
t2 – 8t + 15 = 0
(t-3)(t-5) = 0
t = 3.5
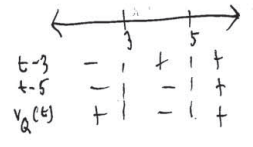
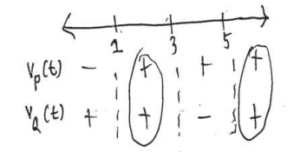
Particles P and Q are moving in the same direction when 1 < t < 3 and 5 < t ≤ 8.
(c)
aQ(t) = 2t – 8
aQ(2) = 2(2) – 8 = -4
The speed of particle Q is decreasing because the particle has a positive velocity but negative acceleration when t = 2.
(d)
@ t = 3, particle Q first changes direction
\({x_{Q}}^{(t)}=\int \left ( t^{2}-8t+15 \right )dt = \frac{t^{3}}{3}-4t^{2}+15t+c\)
\({x_{Q}}^{(0)}=c = 5\Rightarrow {x_{Q}}^{(t)} = \frac{t^{3}}{3}-4t^{2}+15t+5\)
\({x_{Q}}^{(3)}=\frac{3^{3}}{3} -4(3)^{2}+15(3)+5= 9-35+45+5=23\)
Question:
A particle, P, is moving along the x-axis. The velocity of particle P at time t is given by \(v_{p}(t)= sin(t^{1.5})\) for 0 ≤ t ≤ π. At time t = 0, particle P is at position x = 5.
A second particle, Q, also moves along the x-axis. The velocity of particle Q at time t is given by \(v_{Q}(t)\) = (t – 1.8) • 1.25t for 0 ≤ t ≤ π. At time t = 0, particle Q is at position x = 10.
(a) Find the positions of particles P and Q at time t = 1.
(b) Are particles P and Q moving toward each other or away from each other at time t = 1 ? Explain your reasoning.
(c) Find the acceleration of particle Q at time t = 1. Is the speed of particle Q increasing or decreasing at time t = 1 ? Explain your reasoning.
(d) Find the total distance traveled by particle P over the time interval 0 ≤ t ≤ π.
▶️Answer/Explanation
Ans:
(a)
position of \(p = x_{p}=5+\int_{0}^{1}sin(t^{1.5})dt=5+0.37066\)
position of \(Q = x_{Q}=10+\int_{0}^{1}{v_{Q}}^{(t)}dt=8.56435\)
At time t=1, the position of particle p is 5.37066 and the position of particle Q is 8.56435
(b)
\(v_{Q}(1)= -1\) \(X_{Q}(1)= 5.37066\)
\(v_{P}(2) = 0.84147\) \(X_{P}(2) = 8.80035\)
At time t=1 the 2 particles are moving closer to each other because xp(1) = 5.37066 and xQ(1) = 8.56435, which means that particle Q is to the right of particle p at t = 1, and since particle Q has a negative velocity it is moving left and particle p has a positive velocity it is moving right, so the particles are moving toward each other at time t=1.
(c)
\(a_Q\)= acceleration of particle Q
\(a_Q = {v_{Q}}'(1)\) \({v_{Q}}'(1)= 1.02686.\)
\(v_{a}(1)= -1\) Since the \(a_{Q}(1)\) is 1.02686 and is positive and and \(v_{Q}(1)\) is negative, the speed of particle Q at time t=1 must be decreasing.
(d)
Total distance particle P travelled from \(0\leq t\leq \pi =\int_{0}^{\pi }|{v_{p}}^{(t)}|dt=1.93148\)
The total distance particle p travelled from 0 ≤ t ≤ π is 1.93148.
