AP Calculus AB 4.4 Introduction to Related Rates - MCQs - Exam Style Questions
No-Calc Question
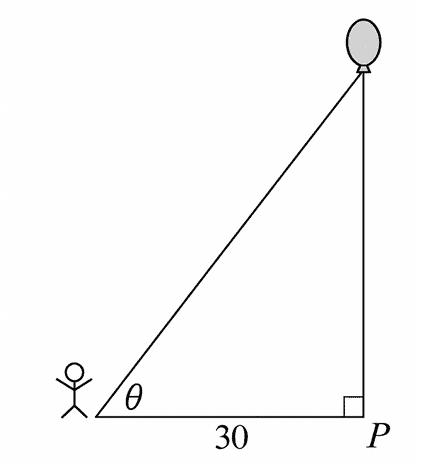
A person stands 30 feet from point \(P\) and watches a balloon rise vertically from the point, as shown in the figure above. The balloon is rising at a constant rate of 2 feet per second. What is the rate of change, in radians per second, of angle \(\theta\) at the instant when the balloon is 40 feet above point \(P\) ?
(A) \(\tfrac{3}{100}\)
(B) \(\tfrac{3}{125}\)
(C) \(\tfrac{1}{12}\)
(D) \(\tfrac{5}{27}\)
(B) \(\tfrac{3}{125}\)
(C) \(\tfrac{1}{12}\)
(D) \(\tfrac{5}{27}\)
▶️ Answer/Explanation
Let \(\tan\theta=\dfrac{y}{30}\).
Differentiate: \(\sec^2\theta\,\dfrac{d\theta}{dt}=\dfrac{1}{30}\dfrac{dy}{dt}\).
At \(y=40\): \(\tan\theta=\dfrac{40}{30}=\dfrac{4}{3}\Rightarrow \sec^2\theta=1+\tan^2\theta=\dfrac{25}{9}\).
Then \(\displaystyle \dfrac{d\theta}{dt}=\frac{(1/30)\cdot 2}{25/9}=\frac{1}{15}\cdot\frac{9}{25}=\frac{3}{125}\).
✅ Answer: (B)
Differentiate: \(\sec^2\theta\,\dfrac{d\theta}{dt}=\dfrac{1}{30}\dfrac{dy}{dt}\).
At \(y=40\): \(\tan\theta=\dfrac{40}{30}=\dfrac{4}{3}\Rightarrow \sec^2\theta=1+\tan^2\theta=\dfrac{25}{9}\).
Then \(\displaystyle \dfrac{d\theta}{dt}=\frac{(1/30)\cdot 2}{25/9}=\frac{1}{15}\cdot\frac{9}{25}=\frac{3}{125}\).
✅ Answer: (B)
