Question
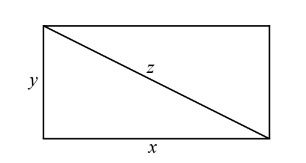
The sides of the rectangle above increase in such a way that \(\frac{dz}{dt}=1 \) = and \(\frac{ dx}{dy}= 3\frac{dy}{dt}\) . At the instant when x = 4 and 3 y = , what is the value of \(\frac{dx}{dt}\)?
(A) \(\frac{1}{3}\) (B) 1 (C) 2 (D)\(\sqrt{5}\) (E) 5
▶️Answer/Explanation
Ans:B
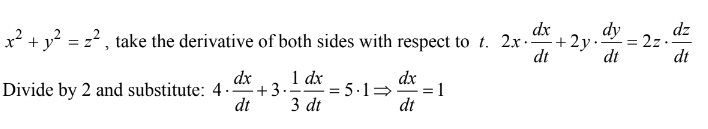
Question
What is the instantaneous rate of change at x = 2 of the function f given by \(f(x)=\frac{x^2-2}{x-1}\) ?
(A) 2 (B) \(\frac{1}{6}\) (C)\(\frac{1}{2}\) (D) 2 (E) 6
▶️Answer/Explanation
Ans:D
\(f'(x)=\frac{(x-1)(2x)-(x^2-2)(1)}{(x-1)^2}; f'(2)\frac{(2-1)(4)-(4-2)(1)}{(2-1)^2}=2\)
Question
The radius of a circle is increasing. At a certain instant, the rate of increase in the area of the circle is numerically equal to twice the rate of increase in its circumference. What is the radius of the circle at that instant?
(A) \(\frac{1}{2}\) (B) 1 (C) 2 (D) 2 (E) 4
▶️Answer/Explanation
Ans:D
Question
An ice sculpture in the form of a sphere melts in such a way that it maintains its spherical shape. The volume of the sphere is decreasing at a constant rate of \(2\pi \)cubic meters per hour. At what rate, in square meters per hour, is the surface area of the sphere decreasing at the moment when the radius is 5 meters? (Note: For a sphere of radius r, the surface area is \(4\pi ^{2}r\) and the volume is \(\frac{4}{3}\pi r^{3} \).
(A) \(\frac{4\pi }{5}\)
(B) \(40\pi \)
(C) \(80\pi ^{2}\)
(D) \(100\pi \)
▶️Answer/Explanation
Ans:A
