Question
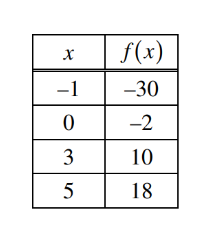
The table above gives selected values for a twice-differentiable function f. Which of the following must be true?
A f has no critical points in the interval -1< x < 5.
B f‘ (x) = 8 for some value of x in the interval -1<x < 5.
C f ‘ (x) > 0 for all values of x in the interval -1<x<5
D f ” (x) < 0 for for all values of x in the interval -1 < x < 5
E The graph of f has no points of inflection in the interval -1< x < 5
▶️Answer/Explanation
Ans:B
Question
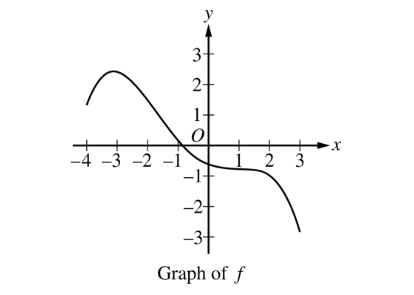
The graph of a differentiable function f is shown above on the closed interval [−4, 3]. How many values of x in the open interval (−4, 3) satisfy the conclusion of the Mean Value Theorem for f on [−4, 3] ?
A Zero
B One
C Two
D Three
▶️Answer/Explanation
Ans:C
Since f is continuous and differentiable, the conditions of the Mean Value Theorem are satisfied on the interval [-4, 3]. As shown in the figure to the right, there are three points in the open interval (-4, 3) where the line tangent to the graph of f is parallel to the secant line through the endpoints of the graph on the interval [-4, 3]. At each of these three points the slopes will be the same and will satisfy f’(c)
Question
Let f be the function given by \(f(x)=x^{3}-2x^{2}+5x-16\) .For what value of x in the closed interval [0,5] does the instantaneous rate of change of f equal the average rate of change of f over that interval?
A 0
B \(\frac{5}{3}\)
C \(\frac{5}{2}\)
D 3
E 5
▶️Answer/Explanation
Ans:D
Question
Let g be a twice-differentiable, increasing function of t. If g(0) = 20 and g(10) = 22 , which of the following must be true on the interval 0 <t< 10?
A g‘(t) = 0 for some t in the interval.
B g‘(t) = 20 for some t in the interval.
C g‘‘(t) = 0 for some t in the interval.
D g‘‘(t) > 0 for all t in the interval.
▶️Answer/Explanation
Ans:B
