Question
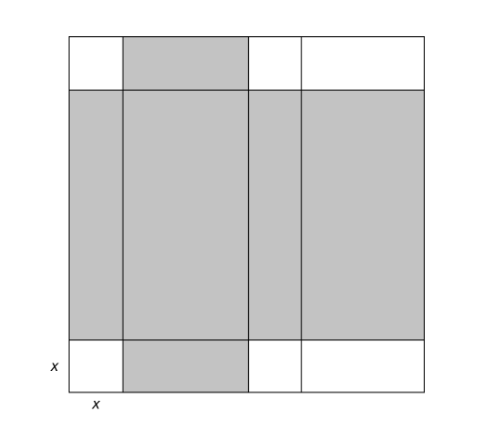
The figure above represents a square sheet of cardboard with side length 20 inches. The sheet is cut and pieces are discarded. When the cardboard is folded, it becomes a rectangular box with a lid. The pattern for the rectangular box with a lid is shaded in the figure. Four squares with side length and two rectangular regions are discarded from the cardboard. Which of the following statements is true? (The volume of a rectangular box is given by V=lwh.)
A When x=10 inches, the box has a minimum possible volume.
B When inches, the box has a maximum possible volume.
C When \(x=\frac{10}{3}\) inches, the box has a minimum possible volume.
D When \(x=\frac{10}{3}\) inches, the box has a maximum possible volume.
Answer/Explanation
Ans:D
To find the volume of the rectangular box, the length, width, and height of the box must be identified. When the shaded region is folded to form the box, the height of the box is x inches. Since the side length of the cardboard sheet is 20 inches, the length of the box is (20−2x) inches because each of the smaller squares has side length . Label the width of the rectangular box as inches. The side length of the cardboard sheet, in inches, can also be defined as x+y+x+y=2x+2y=20, so x+y=10⇒y=10-x is an expression for the width of the box in inches. Therefore, the volume of the box, in cubic inches, is x(20−2x)(10−x). To find the value of x that maximizes the volume, take the derivative of the expression. Since this is a polynomial, it might be easier to expand the polynomial before taking the derivative. This results in \(2x^{3}-40x^{2}+200x\) . Using the power rule, the derivative \(6x^{2}-80x+200\). Factoring this quadratic polynomial as \(2(3x^{2}-40x+100)=2(3x-10)(x-10)=0\Rightarrow x=\frac{10}{3}\) produces the maximum volume of the box.
Question
A rectangular area is to be enclosed by a wall on one side and fencing on the other three sides. If 18 meters of fencing are used, what is the maximum area that can be enclosed?
A \(\frac{9}{2}m^{2}\)
B \(\frac{81}{4}m^{2}\)
C \(27m^{2}\)
D \(40m^{2}\)
E \(\frac{81}{2}m^{2}\)
Answer/Explanation
Ans:E
Question
The speed of a runner, in miles per hour, on a straight trail is modeled by \(f(m)=\frac{1}{10}(-2m^{3}+9m^{2}-12m)+7\), where m is the runner’s distance, in miles, from the start of the trail. What is the maximum speed of the runner for 0 ≤ m ≤ 3 ?
A 6.5
B 6.6
C 7.0
D 7.5
Answer/Explanation
Ans:C
Because f is continuous, the Extreme Value Theorem guarantees the existence of a maximum speed on the closed interval 0 ≤ m ≤ 3, and that absolute maximum will occur at a critical value or at one of the endpoints.
\(f{}'(m)=\frac{1}{10}(-6m^{2}+18m-12)=-\frac{6}{10}(m^{2}-3m+2)=-\frac{6}{10}(m-1)(m-2)\)
(m-1)(m-2)=0
The critical values are m = 1 and m = 2. Therefore the candidates are m = 0, 1, 2, and 3. Evaluate f at each candidate and select the largest .
f(0)=7.0
f(1)=6.5
f(2)=6.6
f(3)=6.1
Question
A puppy weighs 2.0 pounds at birth and 3.5 pounds two months later. If the weight of the puppy during its first 6 months is increasing at a rate proportional to its weight, then how much will the puppy weigh when it is 3 months old?
(A) 4.2 pounds (B) 4.6 pounds (C) 4.8 pounds (D) 5.6 pounds (E) 6.5 pounds
Answer/Explanation
Ans:B
This is an example of exponential growth. We know from pre-calculus that \(w=\left ( \frac{3.5}{2} \right )^{\frac{t}{2}}\) an exponential function that meets the two given conditions. When t=3, w=4.630. Using calculus the student may translate the statement “increasing at a rate proportional to its weight” to mean exponential growth and write the equation w = 2ekt. Using the given
