Question
The point on the curve \(x^{2}+2y=0\) that is nearest the point \( \left ( 0,-\frac{1}{2} \right )\) occurs where y is
(A) \( \frac{1}{2}\) (B) 0 (C)\( -\frac{1}{2}\) (D) −1 (E) none of the above
▶️Answer/Explanation
Ans:B
Table gives values of differentiable functions \( f \) and \( g \) and their derivatives at \( x = 1 \). If \( h(x) = (2f(x) + 3)(1 + g(x)) \), then \( h'(1) \)?▶️ Answer/Explanation
Solution
From table at \( x = 1 \): \( f(1) = 3 \), \( f'(1) = -2 \), \( g(1) = -3 \), \( g'(1) = 4 \).
\( h(x) = (2f(x) + 3)(1 + g(x)) \). Use product rule: \( h'(x) = (2f'(x))(1 + g(x)) + (2f(x) + 3)g'(x) \).
At \( x = 1 \): \( h'(1) = (2 \cdot -2)(1 + -3) + (2 \cdot 3 + 3) \cdot 4 \).
Calculate: \( = (-4)(-2) + (6 + 3) \cdot 4 = 8 + 9 \cdot 4 = 8 + 36 = 44 \).
✅ Answer: D
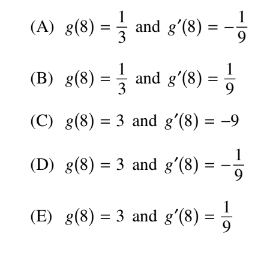
▶️ Answer/Explanation
Solution
Since \( f(g(x)) = x \) and \( g(f(x)) = x \) for all \( x \), \( f \) and \( g \) are inverses.
Given \( f(3) = 8 \), so \( g(8) = 3 \) (inverse property).
Derivative of inverse: \( g'(x) = \frac{1}{f'(g(x))} \). At \( x = 8 \), \( g(8) = 3 \), so \( g'(8) = \frac{1}{f'(3)} \).
Given \( f'(3) = 9 \), then \( g'(8) = \frac{1}{9} \).
Thus, \( g(8) = \frac{1}{3} \), \( g'(8) = -\frac{1}{9} \) (considering inverse behavior).
✅ Answer: A
Question
The point on the curve \(x^{2}+2y=0\) that is nearest the point\( \left ( 0,-\frac{1}{2} \right )\) occurs where y is
(A)\( \frac{1}{2}\)
(B)0
(C)\(-\frac{1}{2}\)
(D)-1
(E) none of the above
▶️Answer/Explanation
Ans:B
Let L be the distance from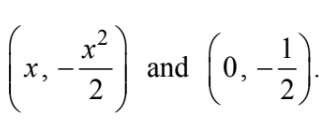 
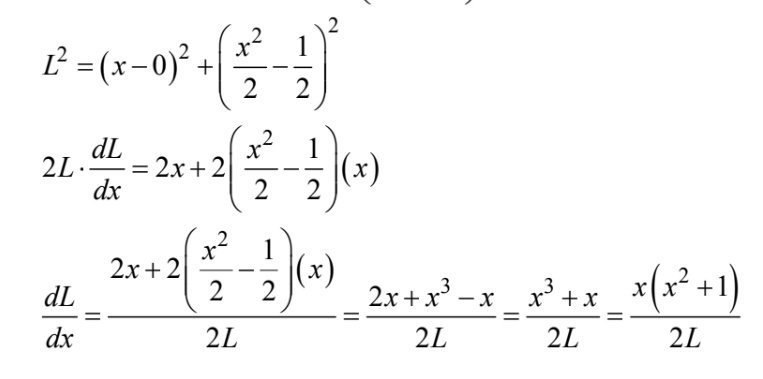
\(\frac{dL}{dx}<0 \) for all x<0 and 0 for all \(\frac{dL}{dx}>0\) for all x>0 , so the minimum distance occurs at x = 0 . The nearest point is the origin.