Question

Train A runs back and forth on an east-west section of railroad track. Train A’s velocity, measured in meters per minute, is given by a differentiable function vA (t) where time t is measured in minutes. Selected values for v A (t) are given in the table above.
(a) Find the average acceleration of train A over the interval 2 ≤ t ≤ 8.
(b) Do the data in the table support the conclusion that train A’s velocity is -100 meters per minute at some time t with 5 < t < 8 ? Give a reason for your answer.
(c) At time t = 2, train A’s position is 300 meters east of the Origin Station, and the train is moving to the east. Write an expression involving an integral that gives the position of train A, in meters from the Origin Station, at time t = 12. Use a trapezoidal sum with three subintervals indicated by the table to approximate the position of the train at time t = 12.
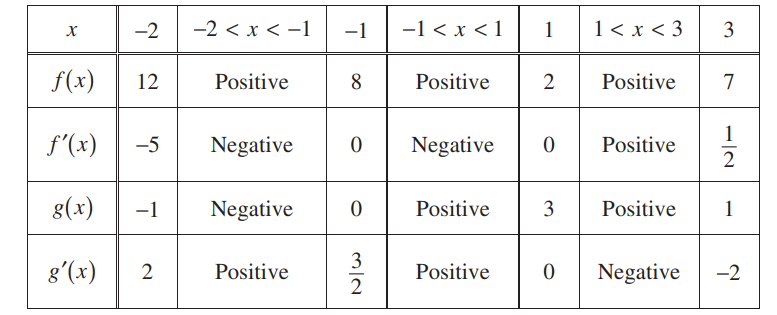
(d) A second train, train B, travels north from the Origin Station. At time t the velocity of train B is given by vB (t) = -5t2 + 60t + 25, and at time t = 2 the train is 400 meters north of the station. Find the rate, in meters per minute, at which the distance between train A and train B is changing at time t = 2.
▶️Answer/Explanation
Ans:
(a)
\(\frac{v(8)-v(2)}{8-2}\rightarrow \frac{-120-100}{6}\rightarrow \frac{-220}{6}\rightarrow \frac{-110}{3}m/min^{2}\)
(b)
Yes, because v(8) = -120 and v(5) = 40 and the function is differentiable and this continuous the train’s velocity must be -100 m/min at some point between 5 < t < 8 accordingly to the intermediate value theorem.
(c)
\(x(12)= \int_{2}^{12}{v_{A}}^{(t)}dt + x(2)\rightarrow x(12)=\int_{2}^{12}{v_{A}}^{(t)}dt +300\)
\(x(12)\approx 3\cdot \frac{1}{2}\cdot (140)+3\cdot \frac{1}{2}\cdot (-80)+4\cdot \frac{1}{2}\cdot (-270)+300\)
210 – 120 – 540 + 300
210 – 240 – 120
-30-120
150 meaning it is 150 m W of origin station
(d)
\(\frac{dB}{dt}= -5t^{2}+60t + 25 \rightarrow 125 m/min\)
-20 + 120 +25
120 + 5 → 135
\(\frac{dA}{dt}= 100 m/min\)
A2 + B2 + = D2
\(2A\frac{dA}{dt}+2B\frac{dB}{dt}=2D\frac{dD}{dt}\)
600(100) + 800 (125) = 1000 \(\frac{dD}{dt}\)
6000 + 100000 = 1000 \(\frac{dD}{dt}\)
\(\frac{160,000}{1000}=\frac{dD}{dt}\rightarrow \frac{dD}{dt}=160 m/min\)
Question:
The twice-differentiable functions f and g are defined for all real numbers x. Values of f, f’, g, and g’ for various values of x are given in the table above.
(a) Find the x-coordinate of each relative minimum of f on the interval [-2, 3] . Justify your answers.
(b) Explain why there must be a value c, for -1 < c < 1, such that f”(c) =0.
(c) The function h is defined by h(x) = In (f(x)). Find h'(3). Show the computations that lead to your answer.
(d) Evaluate \(\int_{-2}^{3}f'(g(x))g'(x)dx.\)
▶️Answer/Explanation
Ans:
(a)
Critical numbers : x = -1, 1
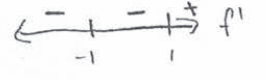
f has a rel. min. at x = 1 because f'(1) = 0 and f’ switches sign from negative to positive there.
(b)
f'(-1) = 0 and f'(1) = 0, and f'(x) is differentiable and continuous on the internal so by rolle’s Theorem there is some value c where f”(c) = 0.
(c)
\(h'(x)=\frac{f'(x)}{f(x)}\)
\(h'(3)=\frac{f'(3)}{f(3)}\)
\(h'(3)=\frac{\frac{1}{0}}{7}\)
\(h'(3)=\frac{1}{2}\cdot \frac{1}{7}\)
\(h'(3)=\frac{1}{14}\)
(d)
u = g(x)
du = g'(x) dx
\(\int f'(u)du\)
\(\left [ f\left ( g(x) \right ) \right ]_{-2}^{3}\)
\(f(g(3)) – f(g(-2))\)
\(f(1) – f(-1)\)
\(2-8\)
\(-6\)
Question:
The rate at which rainwater flows into a drainpipe is modeled by the function R, where \(R(t)=20sin\left ( \frac{t^{2}}{35} \right )\) cubic feet per hour, t is measured in hours, and 0 ≤ t ≤ 8. The pipe is partially blocked, allowing water to drain out the other end of the pipe at a rate modeled by D(t) = -0.04t3 + 0.4t2 + 0.96t cubic feet per hour, for 0 ≤ t ≤ 8. There are 30 cubic feet of water in the pipe at time t = 0.
(a) How many cubic feet of rainwater flow into the pipe during the 8-hour time interval 0 ≤ t ≤ 8?
(b) Is the amount of water in the pipe increasing or decreasing at time t = 3 hours? Give a reason for your answer.
(c) At what time t, 0 ≤ t ≤ 8, is the amount of water in the pipe at a minimum? Justify your answer.
(d) The pipe can hold 50 cubic feet of water before overflowing. For t > 8, water continues to flow into and out of the pipe at the given rates until the pipe begins to overflow. Write, but do not solve, an equation involving one or more integrals that gives the time w when the pipe will begin to overflow.
▶️Answer/Explanation
Ans:
(a)
\(\int_{0}^{8}R(t)dt = \int_{0}^{8}20 sin\frac{t^{2}}{35}dt=76.570ft^{3}\)
During the eight hour interval, about 76.570 cubic feet of water flow into the drainpipe
(b)
Total water : T(x) \(T'(x) = R(x) – F(x) = 20in\frac{t^{2}}{35}+.04t.^{3}-.4t^{2}-.96t\)
T'(3) = 20 in 9/35 + .04(27) – .4(0) – .96(3) : : 314 < 0
after three hours, the amount of water in the pipe is decreasing because the derivative of the amount of water (the difference between water interring and leaving) is less than zero at 3 hours.
(c)
T'(t) = 0 @ t = 0, 3.2716584
\(T(t)=T(0)+\int_{0}^{t}T'(t)dt=30+\int_{0}^{t}T'(t)dt\)
T(0) = 30
T(3.272) = 27.965
T(8) = 48.544
after testing all critical numbers and endpoints for their values, the amount of water in the pipe achieves a minimum value of about 27.965 after about 3.272 hours.
(d)
50 = T(w)
\(50 = 30+\int_{0}^{w}T'(t)dt\)
\(20 = \int_{0}^{w}T'(t)dt=\int_{0}^{w}\left [ R(t)-D(t) \right ]dt\)
Question:
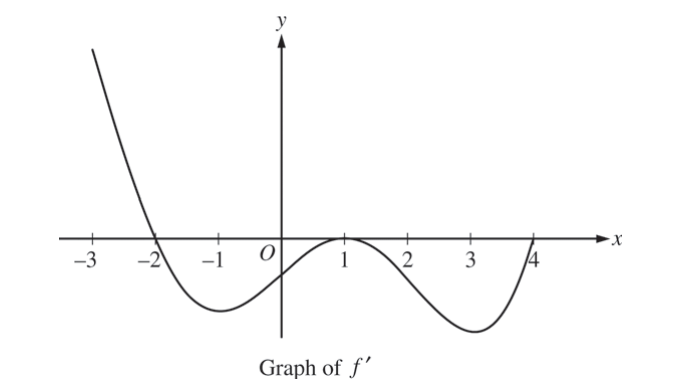
The figure above shows the graph of f’, the derivative of a twice-differentiable function f, on the interval [-3, 4] . The graph of f’ has horizontal tangents at x =- 1, x =1, and x = 3. The areas of the regions bounded by the x-axis and the graph of f’ on the intervals [-2, 1] and [1, 4] are 9 and 12, respectively.
(a) Find all x-coordinates at which f has a relative maximum. Give a reason for your answer.
(b) On what open intervals contained in -3 < x < 4 is the graph of f both concave down and decreasing? Give a reason for your answer.
(c) Find the x-coordinates of all points of inflection for the graph of f. Give a reason for your answer.
(d) Given that f(1) = 3,, write an expression for f(x) that involves an integral. Find f(4) and f(-2).
▶️Answer/Explanation
Ans:
(a)
∴ f(x) has a relative maximum at x = -2 because f'(x) switches from positive to negative of this point.
(b) The graph of f is both concave down and decreasing on the intervals (-2, -1) and (1, 3) because on these intervals f'(x) is negative and also f”(x) is negative.
(c)
x = -1, 1, 3
The x – coordinates of the points of inflection for the graph off f are x = -1, x = 1, x = 3, This is because at these points, f”(x) switches signs.
(d)
\(f(x)=\int_{1}^{x}f'(t)dt+3\)
\(f(4)=\int_{1}^{(4)}f'(t)dt+3\) \(f(-2)=\int_{1}^{(-2)}f'(t)dt+3\)
= (12) + 3 = (9) + 3
f(4) = -9 f(-2) = 12
Question:
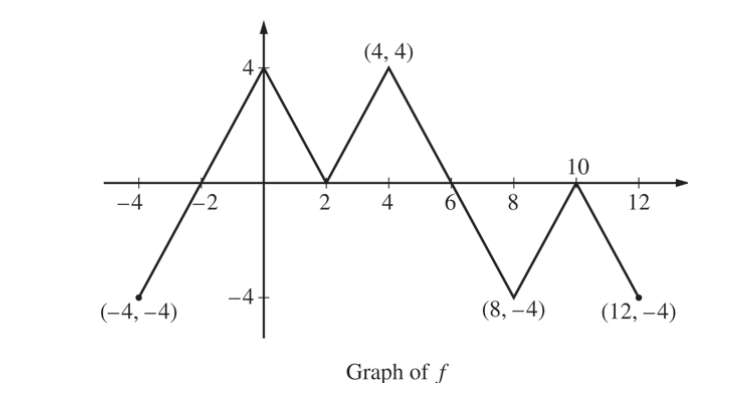
The figure above shows the graph of the piecewise-linear function f. For -4 ≤ x ≤ 12, the function g is defined by\(g(x)=\int_{2}^{x}f(t)dt.\)
(a) Does g have a relative minimum, a relative maximum, or neither at x = 10 ? Justify your answer.
(b) Does the graph of g have a point of inflection at x = 4 ? Justify your answer.
(c) Find the absolute minimum value and the absolute maximum value of g on the interval -4 ≤ x ≤ 12. Justify your answers.
(d) For -4 ≤ x ≤ 12 , find all intervals for which g (x) ≤ 0.
▶️Answer/Explanation
Ans:
(a)
g'(x) = f(x)
g does not have a relative minimum or maximum at x = 10 because g'(x) = f(x) does not change sign at this point.
(b)
g”(x) = f'(x)
f'(x) = g”(x) does change sign at x = 4 so g does have a point of inflection at this point
(c)
g'(x) = f(x) = 0 x = -2 x = 2
x = 6 x = 10
does not change sign at x = 2 and x = 10
The absolute minimum value of g on the interval -4 ≤ x ≤ 12 is -8 and the absolute maximum value of g is 8.
(d)
\(g(x)=\int_{2}^{x}f(t)dt\leq 0\)
g(x) = 0 at x = 2 and x = 10
g(x) ≤ 0 in the intervals -4 ≤ x ≤ 2 and 10 ≤ x ≤ 12
Question:
For t ≥ 0, a particle moves along the x-axis. The velocity of the particle at time t is given by \(v(t)=1+2 sin\left ( \frac{t^{2}}{2} \right )\) The particle is at position x = 2 at time t = 4.
(a) At time t = 4, is the particle speeding up or slowing down?
(b) Find all times t in the interval 0 < t < 3 when the particle changes direction. Justify your answer.
(c) Find the position of the particle at time t = 0.
(d) Find the total distance the particle travels from time t = 0 to time t = 3.
▶️Answer/Explanation
Ans:
(a)
\(v(4)=1+2 sin\left ( \frac{4^{2}}{2} \right )\)
v(4) = 2.979
\(v'(t)=2 cos\left ( \frac{t^{2}}{2} \right )(t)\)
\(v'(4)=2 cos\left ( \frac{4^{2}}{2} \right )(4)\)
v'(4) = -1.164
Showing down because v(A) is positive and v'(4) is negative.
(b)
\(1+2sin\left ( \frac{t^{2}}{2} \right )=0\)
t = 2.707
The particle changes direction one time at t = 2.707 because v(t) = 0 and v(t) changes from positive to negative.
(c)
\(2+\int_{4}^{0}v(t)dt = -3.815\)
(d)
\(2+\int_{0}^{3}|v(t)|dt = 5.301\)
Question:
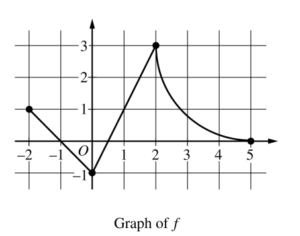
The continuous function f is defined on the closed interval −6 ≤ x ≤ 5. The figure above shows a portion of the graph of f, consisting of two line segments and a quarter of a circle centered at the point (5, 3). It is known that the point \((3,3-\sqrt{5})\) is on the graph of f.
(a) If \(\int_{-6}^{5}f(x)dx=7,\) find the value of \(\int_{-6}^{-2}f(x)dx.\) Show the work that leads to your answer
(b) Evaluate \(\int_{3}^{5}(2f'(x)+4)dx.\)
(c) The function g is given by \(g(x)=\int_{-2}^{x}f(t)dt.\) Find the absolute maximum value of g on the interval − 2 ≤ x ≤ 5. Justify your answer.
(d) Find \(\lim_{x\rightarrow 1}\frac{10^{x}-3f'(x)}{f(x)-arctan x}.\)
▶️Answer/Explanation
Ans:
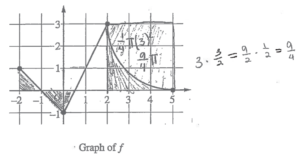
(a)
\(\int_{-6}^{-2}f(x)dx=\int_{-6}^{5}f(x)dx-\int_{-2}^{5}f(x)dx\)
\(\int_{-6}^{-2}f(x)dx=7-\left [ \frac{1}{2}-\frac{1}{2}-\frac{1}{4}+\frac{9}{4}+\left ( 9-\frac{9\pi }{4} \right ) \right ]\)
(b)
\(\int_{3}^{5}2f'(x)+4dx=\int_{3}^{5}2(f'(x)+2)dx\)
\(=2\int_{3}^{5}f'(x)+2dx\)
\(=2\cdot \left [ f(x)+2x \right ]_{3}^{5}\)
\(=2\cdot \left [ \left [ f(5)+2(5) \right ]-\left [ f(3)+2(3) \right ] \right ]\)
(c)
g'(x) = f(x)
g'(x) = f(x) = 0
x = -1, x = 1/2, x = 5
Since f(x) is continuous on -2 ≤ x ≤ 5, then g(x) = \(\int_{-2}^{5}f(t)dt \) is also continuous on -2 ≤ x ≤ 5. Therefore, by the EVT, g(x) has an absolute max. on -2 ≤ x ≤ 5.
Candidates for abs. max : x = -2, -1, 1/2, 5
\(x = -2 : \int_{-2}^{-2}f(t)dt=0\)
\(x = -1 : \int_{-2}^{-1}f(t)dt=\frac{1}{2}\)
\(x = \frac{1}{2} : \int_{-2}^{1/2}f(t)dt=\frac{1}{2}-\frac{1}{2}-\frac{1}{4}=-\frac{1}{4}\)
\(x = 5 : \int_{-2}^{-5}f(t)dt=-\frac{1}{4}+\frac{9}{4}+\left ( 9-\frac{\pi }{4} \right )=2+9-\frac{9\pi }{4}=11-\frac{9\pi }{4}\)
The absolute maximum value of g is \(11-\frac{9\pi }{4}\) and the absolute maximum occurs at x = 5.
(d)
\(\lim_{x\rightarrow 1}10^{x}-3f'(x)=10-3f'(1)=10-3(2)=4\)
\(\lim_{x\rightarrow 1}f(x)-arctan x=1-\frac{\pi }{4}\)
\(arctan(1)=\frac{\pi }{4}\)
\(\lim_{x\rightarrow 1}\frac{10^{x}-3f'(x)}{f(x)-arctan x}=\frac{4}{1-\pi /4}\)
Question
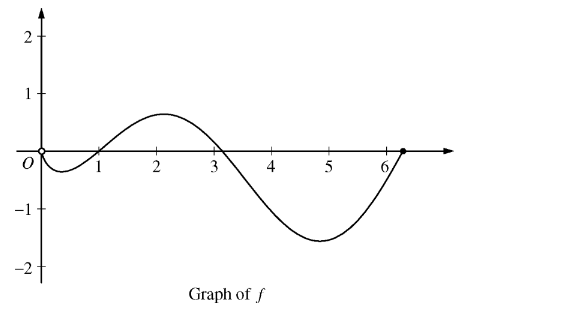
Let f be the function given by f(x)=(Inx)(sinx).The figure above shows the graph of f for \(0<x\leq 2\pi \) The function g is defined by g(x )=\(g(x)=\int_{1}^{x}f(t) dt~ for~ 0<x\leq2 \pi \).
(a) Find g(1) and g'(1)
(b) On what intervals, if any, is g increasing? Justify your answer.
(c) For \(0<x\leq 2\pi \), find the value of x at which g has an absolute minimum. Justify your answer.
(d) For \(0<x\leq 2\pi \) is there a value of x at which the graph of g is tangent to the x-axis? Explain why or why not.
▶️Answer/Explanation
(a)\(g(1)=\int_{1}^{1}f(t)dt=0\) and \(g'(1)=f(1)=0 \)
(b) Since g'(x) = f(x), g is increasing on the interval 1≤ x ≤ because \(f(x) > 0 for 1 < x < \pi.\)
(c) For\( 0 < x < 2\pi, g'(x) = f(x) = 0\) when \(x = 1, \pi\) . \({g}’ f\) changes from negative to positive only at x = 1. The absolute minimum must occur at x = 1 or at the right endpoint. Since \(g(1) = 0\) and \(g(2\pi)=\int_{1}^{2\pi}f(t)dt=\int_{1}^{\pi}f(t)dt+\int_{\pi}^{2\pi}f(t)<0\) by comparison of the two areas, the absolute minimum occurs at \(x = 2π.\)
(d) Yes, the graph of g is tangent to the x-axis at x = 1 since g(1) = 0 and g'(1) = 0.
Question
Let g(x )=\(xe^{-x}+be^{-x}\), where b is a positive constant.
(a) Find\( \lim_{x\rightarrow \infty }g(x)\)
(b) For what positive value of b does g have an absolute maximum at \(x=\frac{2}{3}\)? Justify your answer.
(c) Find all values of b, if any, for which the graph of g has a point of inflection on the interval \(0 < x <\infty\). Justify your answer.
▶️Answer/Explanation
(a)\(\lim_{x\rightarrow \infty }g(x)=0\)
(b)\(g'(x)=e^{-x}-xe^{-x}-be^{-x}=(1-x-b)e^{-x}\)
\(g’\left ( \frac{2}{3} \right )=\left ( \frac{1}{3}-b \right )e^{2/3}=0\Rightarrow b=\frac{1}{3}\)when \(b=\frac{1}{3},g'(x)=\left ( \frac{2}{3}-x \right )e^{-x}\)
for\(x<\frac{2}{3},g'(x)>0 \) and for\( x>\frac{2}{3},g'(x)<0\) Therefore, when\( b =\frac{1}{3}\),g has an absolute maximum at \(x=\frac{2}{3}.
(c) g”(x) = −e^{-x} (1 − x – b)e^{-x} = (x −2+b)e^{-x} \)
If\( 0 <b< 2, then g”(x) \)will change sign at x = 2 − b > 0. Therefore, the graph of g will have a point of inflection on the interval 0 < x < ∞ when 0 < b < 2.