AP Calculus AB: 5.3 Determining Intervals on Which a Function Is Increasing or Decreasing

AP PhysicsAP Calculus AP ChemistryAP Biology

Question

The function f is continuous on the closed interval [0,5]. The graph of f′, the derivative of f, is shown above. On which of the following intervals is f increasing?

A $open bracket, 0 comma 1, close bracket$ and $open bracket, 2 comma 4, close bracket$

B [0,1] and [3,5]

C $open bracket, 0 comma 1, close bracket$ and $open bracket, 4 comma 5, close bracket$ only

D $open bracket, 0 comma 2, close bracket$ and $open bracket, 4 comma 5, close bracket$

▶️Answer/Explanation

Ans:D

The function $f$

f

is increasing on closed intervals where $f^{'}$

f^{'}

is positive on the corresponding open intervals. The graph indicates that $f prime of x, is greater than 0$ on the intervals $open parenthesis, 0 comma 2, close parenthesis$

(0, 2)

and $open parenthesis, 4 comma 5, close parenthesis$

(4, 5)

, so $f$

f

is increasing on the intervals $open bracket, 0 comma 2, close bracket$

[0, 2]

and $open bracket, 4 comma 5, close bracket$

[4, 5]

Question

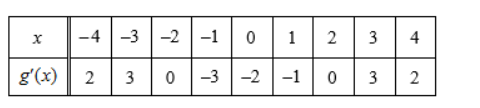
The derivative g’ of a function g is continuous and has exactly two zeros. Selected values of g’ are given in the table above. If the domain of g is the set of all real numbers, then g is decreasing on which of the following intervals

A -2 ≤ x ≤ 2 only

B -1 ≤ x ≤ 1 only

C x ≥ -2

D x ≥ 2 only

E x ≤ -2 or x ≥ 2

▶️Answer/Explanation

Ans:A

Question

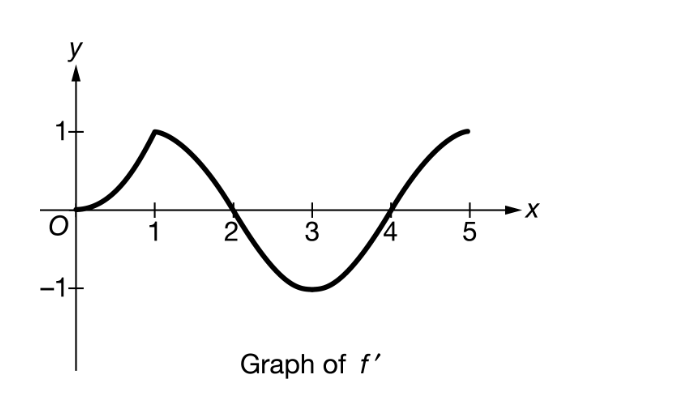
The function $f$

$f$

is continuous on the closed interval $open bracket, 0 comma 5, close bracket$ . The graph of $f^{'}$

$'$

, the derivative of $f$

$f$

, is shown above. On which of the following intervals is $f$ increasing?

$A [0, 1]$

and $open bracket, 2 comma 4, close bracket$

B [0,1] and [3,5]

C $open bracket, 0 comma 1, close bracket$ and $open bracket, 4 comma 5, close bracket$ only

D $open bracket, 0 comma 2, close bracket$ and $open bracket, 4 comma 5, close bracket$

▶️Answer/Explanation

Ans:D
The function $f$

f

is increasing on closed intervals where $f^{'}$

'

is positive on the corresponding open intervals. The graph indicates that $f prime of x, is greater than 0$ on the intervals $open parenthesis, 0 comma 2, close parenthesis$ nd $open parenthesis, 4 comma 5, close parenthesis$ , so $f$

f

is increasing on the intervals $open bracket, 0 comma 2, close bracket$ and $open bracket, 4 comma 5, close bracket$ .

Question

Let f be the function given by $f (x) = 3 - 2 x$ . If g is a function with derivative given by $g^{'} (x) = f (x) f^{'} (x) (x - 3)$ , on what intervals is g increasing?

A $(-\infty ,\frac{3}{2}]$ and $[3,\infty )$

B $(-\infty ,\frac{3}{2}]$ only

C $[\frac{3}{2},3]$ only

D $[\frac{3}{2},\infty )$

E $[3,\infty )$ only

▶️Answer/Explanation

Ans:A

AP Calculus AB: 5.3 Determining Intervals on Which a Function Is Increasing or Decreasing – Exam Style questions with Answer- MCQ

Question

Question

Question

Question

Resources

Members

Company