Question
The function g is differentiable and satisfies g(−1)=4 and g′(−1)=2. What is the approximation of g(−1.2) using the line tangent to the graph of g at x=−1
A 3.6
B 3.8
C 4.2
D 4.4
▶️Answer/Explanation
Ans:A
An equation of the line tangent to the graph of g at x=a is y=g(a)+g′(a)(x−a). In this question, a=−1. The value of y when x=−1.2 would be an approximation to g(−1.2).
g(−1.2)≈g(−1)+g′(−1)(−1.2−(−1))=4+2(−0.2)=3.6
Question
Let f be the function given by \(f(x)=x^{3}-6x^{2}-15x\). What is the maximum value of f on the interval [0,6]?
A 0
B 5
C 6
D 8
▶️Answer/Explanation
Ans:A
Question
33. The absolute maximum value of\(f(x)=x^{3}-3x^{2}+12\) on the closed interval [−2, 4] occurs at x =
(A) 4 (B) 2 (C) 1 (D) 0 (E) –2
▶️Answer/Explanation
Ans:A
Check the critical points and the endpoints.
\(f'(x) = 3x^2 − 6x = 3x(x − 2)\) so the critical points are 0 and 2.
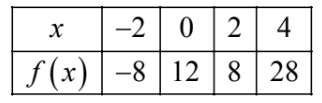
Absolute maximum is at x = 4.
Question
The absolute maximum values of \(f(x)=x^{3}-3x^{2}+12\) on the closed interval [−2, 4] occurs at x =
A 4
B 2
C 1
D 0
E -2
▶️Answer/Explanation
Ans:A
