Question:
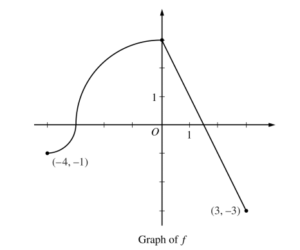
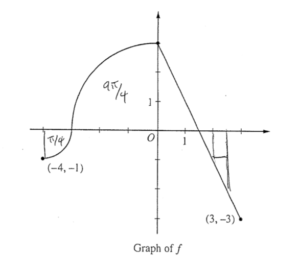
The continuous function f is defined on the interval -4 ≤ x ≤ 3. The graph of f consists of two quarter circles and one line segment, as shown in the figure above. Let \(g(x)=2x+\int_0^x f(t)dt\).
(a) Find g(-3) . Find g'(x) and evaluate g'(-3) .
(b) Determine the x-coordinate of the point at which g has an absolute maximum on the interval -4 ≤ x ≤ 3. Justify your answer.
(c) Find all values of x on the interval -4 ≤ x ≤ 3 for which the graph of g has a point of inflection. Give a reason for your answer.
(d) Find the average rate of change of f on the interval-4 ≤ x ≤ 3. There is no point c, -4 < c < 3, for which f'(c) is equal to that average rate of change. Explain why this statement does not contradict the Mean Value Theorem.
▶️Answer/Explanation
Ans:
(a)
\(g(-3)=2(-3)+\int_{0}^{-3}f(t)dt = -6 -\frac{9\pi }{4}\)
\(g'(x)=\frac{d}{dx}\left ( 2x + \int_{0}^{x}f(t)dt \right )=2+f(x)\)
g'(-3) = 2 + f(-3) = 2 + 0 = 2
(b)
g'(x) = 0 2 + f(x) = 0
g'(x) f(x) = -2
x = 5/2
\(g(-4)=-8+\int_{0}^{-4}f(t)dt\)
= -8 – 2π
\(g(5/2)= 5+\int^{\frac{5}{2}}_{0} f(t)dt = + \frac{5}{4}\)
\(g(3)= 6+\int_{0}^{3}f(t)dt = 6\)
x = 5/2 , because g’ going from t to – proves it as the only relative maximum and g(5/2) is greater than g at either endpoint.
(c)
f'(x) g”(x) = d/dx (g(x)) = f'(x)
The only point of inflection for g is at x = 0, since f'(x), which is equivalent to g”, only changes signs at x = 0 on the interval -4 ≤ x ≤ 3
(d)
Avg. Rate of change = \(\frac{f(3)-f(-4)}{3-4}\)
\(\frac{-3-1}{3+4}=\frac{-2}{7}\)
Because mean value Theorem only applies when the function is continuous And differentiable on the interval, which doesn’t apply here since f(x) isn’t differentiable at x = 0.
Question:
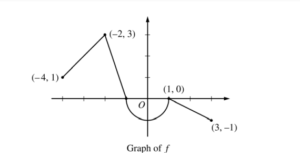
Let f be the continuous function defined on [-4, 3] whose graph, consisting of three line segments and a semicircle centered at the origin, is given above. Let g be the function given by \(g(x)=\int_1^x f(t) dt\).
(a) Find the values of g(2) and g(-2).
(b) For each of g'(-3) and g”(-3) , find the value or state that it does not exist.
(c) Find the x-coordinate of each point at which the graph of g has a horizontal tangent line. For each of these points, determine whether g has a relative minimum, relative maximum, or neither a minimum nor a maximum at the point. Justify your answers.
(d) For -4 < x < 3, find all values of x for which the graph of g has a point of inflection. Explain your reasoning.
▶️Answer/Explanation
Ans:
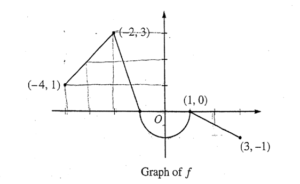
(a)
\(g(2)= \int_{1}^{2}f(t)dt\)
\(g(2)= \frac{-1}{2}(1)\left ( \frac{1}{2} \right )\)
\(g(2)= -\frac{1}{4}\)
\(g(-2)= \int_{1}^{-2}f(t)dt\)
\(g(-2)= \frac{1}{2}\pi(1)^{2}-\left ( \frac{1}{2}(1)(3) \right )\)
\(g(-2)= \frac{\pi -3}{2}\)
(b)
g'(x) = f(x)
g'(-3) = 2
g”(x) = f'(x)
g”(-3) = 1
(c)
g'(x) = f(x) = 0
x = -1 , 1
At x = -1 g has a relative maximum because g'(x) = f(x) changes from positive to negative at x = 1 g has neither because g'(x) = f(x) does not change sign
(d)
g has inflection points where g”(x) = f'(x) changes sign. This occurs at x = -2 , 0 , 1
Question:
A particle moves along a straight line. For 0 ≤ t ≤ 5, the velocity of the particle is given by \(v(t)= -2 + (t^{2}+3t)^{6/5} – t^{3}\), and the position of the particle is given by s(t). It is known that s(0) = 10.
(a) Find all values of t in the interval 0 ≤ t ≤ 4 for which the speed of the particle is 2.
(b) Write an expression involving an integral that gives the position s(t). Use this expression to find the position of the particle at time t = 5.
(c) Find all times t in the interval 0 ≤ t ≤ 5 at which the particle changes direction. Justify your answer.
(d) Is the speed of the particle increasing or decreasing at time t = 4 ? Give a reason for your answer.
▶️Answer/Explanation
Ans:
(a)
|v(t) | = 2 2 ≤ t ≤ 4
t = 3.128, 3.473
(b)
\(s(t)= 10 + \int_{0}^{t}v(x)dx\)
\(s(5)= 10 + \int_{0}^{5}v(x)dx = -9.207\)
(c)
v(t) = 0
t = 0.536 , 3.318
the particle changes direction at 0.536 because v(t) < 0 for (0, 0.536) and v(t) > 0 for (0.536, 3.318). The particle changes direction at 3.318 because v(t) > 0 for (0.536, 3.318) and v(t) < 0 for t> 3.318
(d)
v(4) < 0
a(4) = v'(4) <0
The speed is increasing at t = 4 because both v(4) and a(4) = v'(4) are negative.
Question:
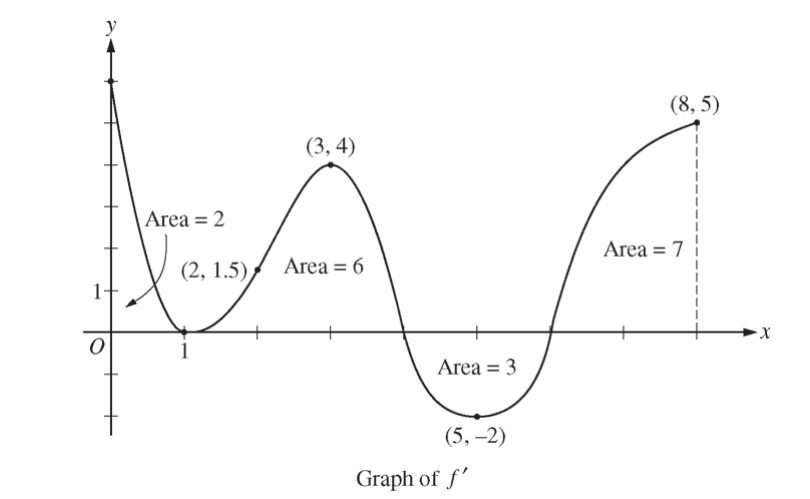
The figure above shows the graph of f’, the derivative of a twice-differentiable function f, on the closed interval 0 ≤ x ≤ 8. The graph of f’ has horizontal tangent lines at x = 1, x = 3, and x = 5. The areas of the regions between the graph of f’ and the x-axis are labeled in the figure. The function f is defined for all real numbers and satisfies f (8) = 4.
(a) Find all values of x on the open interval 0 < x < 8 for which the function f has a local minimum. Justify your answer.
(b) Determine the absolute minimum value of f on the closed interval 0 ≤ x ≤ 8. Justify your answer.
(c) On what open intervals contained in 0 < x < 8 is the graph of f both concave down and increasing? Explain your reasoning.
(d) The function g is defined by \(g(x)=(f(x))^{3}\), if \(f(3)= -\frac{5}{2},\) find the slope of the line tangent to the graph of g at x = 3.
▶️Answer/Explanation
Ans:
(a)
X = 6
f has a local minmum at x = 6, because the graph of f’ changes from negative to positive at x = 6, so using the first derivative test and f has a critical number at x = 6, f has a local minimum
(b)
local minimum = x = 6 f(8) = 4
\(f(6)\rightarrow \int_{6}^{8}f'(x)dx = 7 = f(8)-f(6)=4-f(6)\) f(6) = -3
\(f(0)\rightarrow \int_{0}^{8}f'(x) = 12 = f(8)-f(0)=4-f(0)\) f(0) = -8
The absolute minimum value of f on the interval 0 ≤ x ≤ 8 is -8 because it is the lowest value for the among the endpoints and critical numbers.
(c) \({f}” < 0\)
The open intervals where the graph of f is both concave down and increasing is (0, 1) u (3, 4), or 0 < x < 1 and 3 < x 4, because using the graph of f’, when the graph of f’ is positive and the slope of f’ is negative that means that f is increasing and f” is negative so f is both concave down and increasing.
(d)
g'(x) = 3 (f(x))2. f'(x)
g'(3) = 3 (f(3))2 . f'(3) = 3 (-5/2)2 . (4)
= 3 (25/4)4 = 75
g'(3) = 75
Question:
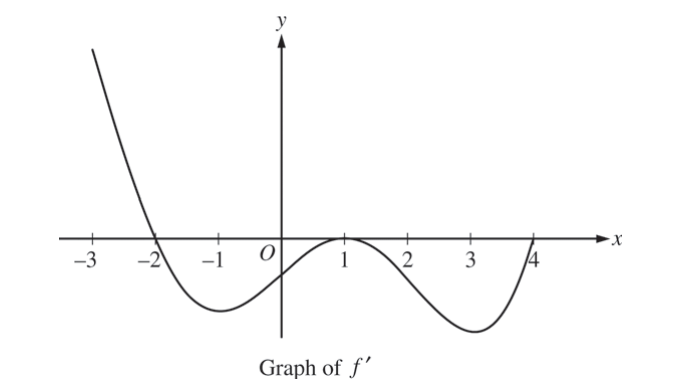
The figure above shows the graph of f’, the derivative of a twice-differentiable function f, on the interval [-3, 4] . The graph of f’ has horizontal tangents at x =- 1, x =1, and x = 3. The areas of the regions bounded by the x-axis and the graph of f’ on the intervals [-2, 1] and [1, 4] are 9 and 12, respectively.
(a) Find all x-coordinates at which f has a relative maximum. Give a reason for your answer.
(b) On what open intervals contained in -3 < x < 4 is the graph of f both concave down and decreasing? Give a reason for your answer.
(c) Find the x-coordinates of all points of inflection for the graph of f. Give a reason for your answer.
(d) Given that f(1) = 3,, write an expression for f(x) that involves an integral. Find f(4) and f(-2).
▶️Answer/Explanation
Ans:
(a)
∴ f(x) has a relative maximum at x = -2 because f'(x) switches from positive to negative of this point.
(b) The graph of f is both concave down and decreasing on the intervals (-2, -1) and (1, 3) because on these intervals f'(x) is negative and also f”(x) is negative.
(c)
x = -1, 1, 3
The x – coordinates of the points of inflection for the graph off f are x = -1, x = 1, x = 3, This is because at these points, f”(x) switches signs.
(d)
\(f(x)=\int_{1}^{x}f'(t)dt+3\)
\(f(4)=\int_{1}^{(4)}f'(t)dt+3\) \(f(-2)=\int_{1}^{(-2)}f'(t)dt+3\)
= (12) + 3 = (9) + 3
f(4) = -9 f(-2) = 12
Question:
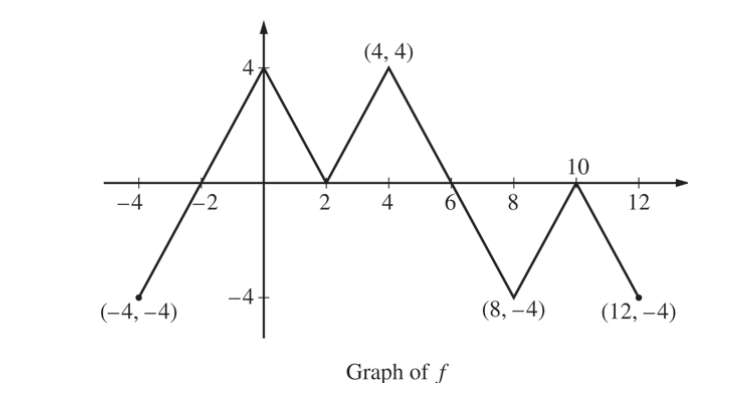
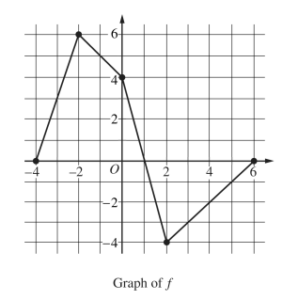
The figure above shows the graph of the piecewise-linear function f. For -4 ≤ x ≤ 12, the function g is defined by\(g(x)=\int_{2}^{x}f(t)dt.\)
(a) Does g have a relative minimum, a relative maximum, or neither at x = 10 ? Justify your answer.
(b) Does the graph of g have a point of inflection at x = 4 ? Justify your answer.
(c) Find the absolute minimum value and the absolute maximum value of g on the interval -4 ≤ x ≤ 12. Justify your answers.
(d) For -4 ≤ x ≤ 12 , find all intervals for which g (x) ≤ 0.
▶️Answer/Explanation
Ans:
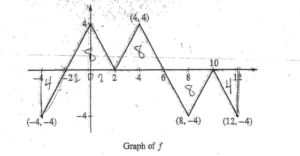
(a)
g'(x) = f(x)
g does not have a relative minimum or maximum at x = 10 because g'(x) = f(x) does not change sign at this point.
(b)
g”(x) = f'(x)
f'(x) = g”(x) does change sign at x = 4 so g does have a point of inflection at this point
(c)
g'(x) = f(x) = 0 x = -2 x = 2
x = 6 x = 10
does not change sign at x = 2 and x = 10
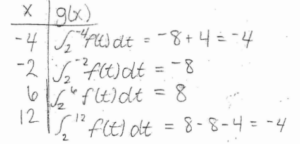
The absolute minimum value of g on the interval -4 ≤ x ≤ 12 is -8 and the absolute maximum value of g is 8.
(d)
\(g(x)=\int_{2}^{x}f(t)dt\leq 0\)
g(x) = 0 at x = 2 and x = 10
g(x) ≤ 0 in the intervals -4 ≤ x ≤ 2 and 10 ≤ x ≤ 12
Question:
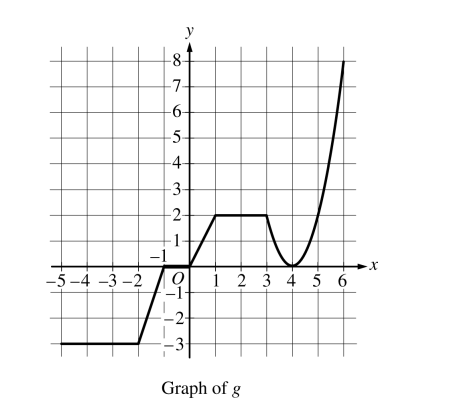
The graph of the continuous function g, the derivative of the function f, is shown above. The function g is piecewise linear for − 5 ≤ x ≤ 3 , and g(x) = 2 ( x− 4)2 for 3 ≤ x ≤ 6.
(a) If f (1) = 3, what is the value of f (−5) ?
(b) Evaluate \(\int_{1}^{6}g(x)dx\) .
(c) For − 5 ≤ x ≤ 6, on what open intervals, if any, is the graph of f both increasing and concave up? Give a reason for your answer.
(d) Find the x-coordinate of each point of inflection of the graph of f. Give a reason for your answer.
▶️Answer/Explanation
Ans:
(a)
f'(x) = g(x)
\(f(x)=\int_{1}^{x}g(t)dt+3\)
\(f(-5)=-\int_{-5}^{1}g(t)dt+3\)
\(f(-5)=-\left ( \frac{1}{2} (1)(2)-\frac{1}{2} (1)(3)-(3)(3)\right )+3\)
\(f(-5)=-\left ( 1-\frac{3}{2}-9\right )+3\)
\(f(-5)=8+\frac{3}{2}+3\)
\(f(-5)=11+\frac{3}{2}\)
(b)
\(\int_{1}^{6}g(x)dx=\int_{1}^{3}g(x)dx+\int_{3}^{6}g(x)dx\)
\(\int_{1}^{6}g(x)dx=(2)(2)+\int_{3}^{6}2(x-4)^{2}dx\)
\(\int_{1}^{6}g(x)dx=4+\left ( \frac{2}{3}(x-4)^{3} \right )|_{3}^{6}\)
\(\int_{1}^{6}g(x)dx=4+\left ( \frac{2}{3}(8)- \frac{2}{3}(-1)\right )\)
\(\int_{1}^{6}g(x)dx=4+\frac{16}{3}+\frac{2}{3}\)
\(\int_{1}^{6}g(x)dx=10\)
(c)
On the interval (0, 1) u(4, 6) f is both increasing and concave up since f'(x) = g(x) and g is positive on the that interval meaning f is increasing on that interval, and g is increasing on that interval, meaning f”(x)>0 on that interval, therefore f is concave up on that interval
(d)
f has a point of inflection at x = 4 since f'(x) = g(x) and since a switches from decreasing to increasing at x = 4, therefore f”(x) = 0 at that point and would change signs from (-) to (+) at x = 4, therefore x = 4 is an inflection point.
Question:
Let f be a continuous function defined on the closed interval −4 ≤ x ≤ 6. The graph of f , consisting of four line segments, is shown above. Let G be the function defined by \(G(x)=\int_{0}^{x}f(t)dt.\)
(a) On what open intervals is the graph of G concave up? Give a reason for your answer.
(b) Let P be the function defined by P (x) = G (x)• f(x). Find P'(3 ).
(c) Find \(\lim_{x\rightarrow 2}\frac{G(x)}{x^{2}-2x}.\)
(d) Find the average rate of change of G on the interval [−4, 2]. Does the Mean Value Theorem guarantee a value c, −4 < c < 2, for which G'(c) is equal to this average rate of change? Justify your answer.
▶️Answer/Explanation
Ans:
(a)
G'(x) = f(x)
G”(x) = f'(x)
On (-4, -2) and (2, 6), G(x) is concave up because f(x) (which is equal to G'(x)) has a positive slope / is increasing.
(b)
p'(x) = G'(x) f(x) + f'(x) G(x)
p'(3) = G'(3) f(3) + f'(3) G(3)
G'(x) = f(x) \(G(3)=\int_{0}^{3}f(t)dt=-\frac{7}{2}\)
\(p'(3)=(-3)(-3)+(1)\left (- \frac{7}{2} \right )\)
(c)
\(\lim_{x\rightarrow 2}G(x)=\lim_{x\rightarrow 2}(x^{2}-2x)=0\) Must be I’hopital’s rule
\(\int_{0}^{2}f(t)dt=0\)
\(\lim_{x\rightarrow 2}\frac{G'(x)}{2x-2}=\frac{f(2)}{4-2}=\frac{-4}{2}\)
(d)
\(\int_{0}^{2}f(t)dt\) \(\int_{0}^{-4}f(t)dt= -(3+9+3+1)\)
= -16
AROC of \(G = \frac{G(2)-G(-4)}{2-(-4)}=\frac{0-(16)}{2+4}=\frac{16}{6}=\frac{8}{3}\)
The meanvalue theorem does guarantee a value of -4<c<2, for which G'(c) is equal to average rate of chang. This is because G'(x) = f(t) and x = t exists for all values, -4<x=+t<2, meaning that G(x) is continuous on the closed interval and differentiable on the open interval.