Question:
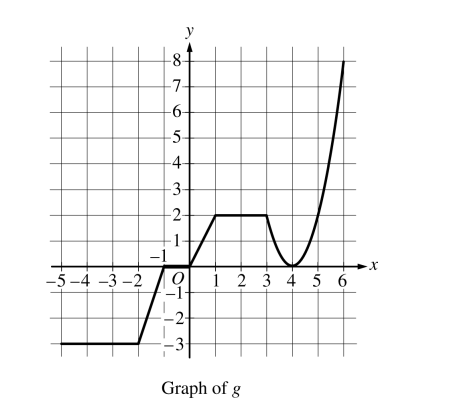
The graph of the continuous function g, the derivative of the function f, is shown above. The function g is piecewise linear for − 5 ≤ x ≤ 3 , and g(x) = 2 ( x− 4)2 for 3 ≤ x ≤ 6.
(a) If f (1) = 3, what is the value of f (−5) ?
(b) Evaluate \(\int_{1}^{6}g(x)dx\) .
(c) For − 5 ≤ x ≤ 6, on what open intervals, if any, is the graph of f both increasing and concave up? Give a reason for your answer.
(d) Find the x-coordinate of each point of inflection of the graph of f. Give a reason for your answer.
▶️Answer/Explanation
Ans:
(a)
f'(x) = g(x)
\(f(x)=\int_{1}^{x}g(t)dt+3\)
\(f(-5)=-\int_{-5}^{1}g(t)dt+3\)
\(f(-5)=-\left ( \frac{1}{2} (1)(2)-\frac{1}{2} (1)(3)-(3)(3)\right )+3\)
\(f(-5)=-\left ( 1-\frac{3}{2}-9\right )+3\)
\(f(-5)=8+\frac{3}{2}+3\)
\(f(-5)=11+\frac{3}{2}\)
(b)
\(\int_{1}^{6}g(x)dx=\int_{1}^{3}g(x)dx+\int_{3}^{6}g(x)dx\)
\(\int_{1}^{6}g(x)dx=(2)(2)+\int_{3}^{6}2(x-4)^{2}dx\)
\(\int_{1}^{6}g(x)dx=4+\left ( \frac{2}{3}(x-4)^{3} \right )|_{3}^{6}\)
\(\int_{1}^{6}g(x)dx=4+\left ( \frac{2}{3}(8)- \frac{2}{3}(-1)\right )\)
\(\int_{1}^{6}g(x)dx=4+\frac{16}{3}+\frac{2}{3}\)
\(\int_{1}^{6}g(x)dx=10\)
(c)
On the interval (0, 1) u(4, 6) f is both increasing and concave up since f'(x) = g(x) and g is positive on the that interval meaning f is increasing on that interval, and g is increasing on that interval, meaning f”(x)>0 on that interval, therefore f is concave up on that interval
(d)
f has a point of inflection at x = 4 since f'(x) = g(x) and since a switches from decreasing to increasing at x = 4, therefore f”(x) = 0 at that point and would change signs from (-) to (+) at x = 4, therefore x = 4 is an inflection point.
Question
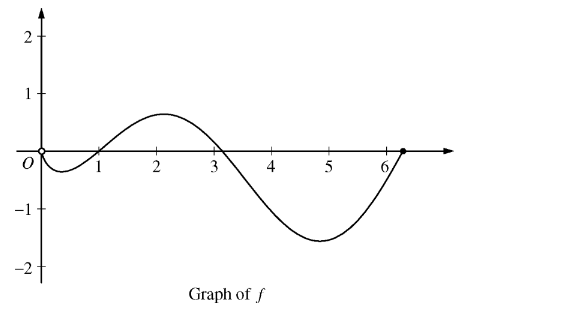
Let f be the function given by f(x)=(lnx)(sinx).The figure above shows the graph of f for \(0<x\leq 2\pi \) The function g is defined by g(x )=\(g(x)=\int_{1}^{x}f(t) dt~ for~ 0<x\leq2 \pi \).
(a) Find g(1) and g'(1)
(b) On what intervals, if any, is g increasing? Justify your answer.
(c) For \(0<x\leq 2\pi \), find the value of x at which g has an absolute minimum. Justify your answer.
(d) For \(0<x\leq 2\pi \)is there a value of x at which the graph of g is tangent to the x-axis? Explain why or why not.
▶️Answer/Explanation
(a)\(g(1)=\int_{1}^{1}f(t)dt=0\) and \(g'(1)=f(1)=0 \)
(b)Since g'(x) = f(x), g is increasing on the interval 1≤ x ≤ because \(f(x) > 0~ for~ 1 < x < \pi.\)
(c) For\( 0 < x < 2\pi, g'(x) = f(x) = 0\) when \(x = 1, \pi\) . g’ f changes from negative to positive only at x = 1. The absolute minimum must occur at x = 1 or at the right endpoint. Since g(1) = 0 and \(g(2\pi)=\int_{1}^{2\pi}f(t)dt=\int_{1}^{\pi}f(t)dt+\int_{\pi}^{2\pi}f(t)<0\) by comparison of the two areas, the absolute minimum occurs at \(x = 2π.\)
(d) Yes, the graph of g is tangent to the x-axis at x = 1 since g(1) = 0 and g'(1) = 0.
Question
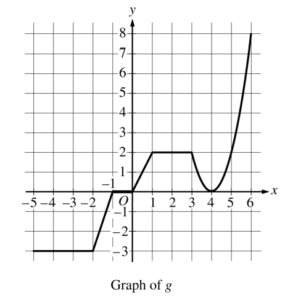
The graph of the continuous function g, the derivative of the function f, is shown above. The function g is piecewise linear for −5 ≤ x < 3, and g (x) = 2(x −4 ) 2 for 3 ≤ x ≤ 6.
(a) If f (1) = 3, what is the value of f(−5) ?
(b) Evaluate \(\int_{1}^{6}g(x)dx.\)
(c) For −5 < x < 6, on what open intervals, if any, is the graph of f both increasing and concave up? Give a reason for your answer.
(d) Find the x-coordinate of each point of inflection of the graph of f. Give a reason for your answer.
▶️Answer/Explanation
Ans:
(a) \(f(-5)=f(1)+\int_{1}^{-5}g(x)dx=f(1)-\int_{-5}^{1}g(x)dx\)
\(=3-\left ( -9-\frac{3}{2}+1 \right )=3-\left ( -\frac{19}{2} \right )=\frac{25}{2}\)
(b) \(\int_{1}^{6}g(x)dx=\int_{1}^{3}g(x)dx+\int_{3}^{6}g(x)dx\)
\(=\int_{1}^{3}2dx+\int_{3}^{6}2(x-4)^{2}dx\)
\(=4+_{x=3}\left [ \frac{2}{3}(x-4)^{3} \right ]^{x=6}=4+\frac{16}{3}-\left ( -\frac{2}{3} \right )=10\)
(c) The graph of f is increasing and concave up on 0 < x < 1 and 4 < x < 6 because f ‘(x) =g(x)> 0 and f ‘(x) = g(x) is increasing on those intervals.
(d) The graph of f has a point of inflection at x = 4 because f'(x) = g(x) changes from decreasing to increasing at x = 4.
Question
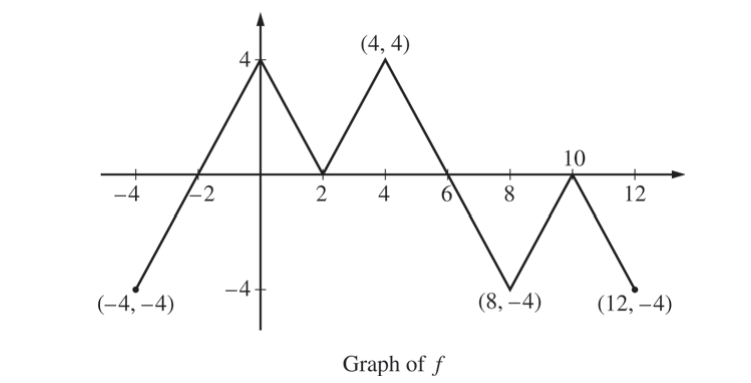
The figure above shows the graph of the piecewise-linear function f. For -4 ≤ x ≤ 12, the function g is defined by \(g(x)=\int_{2}^{x}f(t)dt.\)
(a) Does g have a relative minimum, a relative maximum, or neither at x = 10 ? Justify your answer.
(b) Does the graph of g have a point of inflection at x = 4 ? Justify your answer.
(c) Find the absolute minimum value and the absolute maximum value of g on the interval -4 ≤ x ≤ 12. Justify your answers.
(d) For -4 ≤ x ≤ 12, find all intervals for which g(x) ≤ 0.
▶️Answer/Explanation
Ans:
(a) The function g has neither a relative minimum nor a relative maximum at x = 10 since g′ (x)= f(x) and f (x) ≤ 0 for 8 ≤ x ≤ 12.
(b) The graph of g has a point of inflection at x = 4 since g′(x) = f(x) is increasing for 2 ≤ x ≤ 4 and decreasing for 4 ≤ x ≤ 8.
(c) g′(x) = f(x) changes sign only at x = −2 and x = 6.
| x | g(x) |
-4 -2 6 12 | -4 -8 8 -4 |
On the interval −4 ≤ x ≤ 12, the absolute minimum value is g(−2) =− 8 and the absolute maximum value is g(6) = 8.
(d) g(x) ≤ 0 for −4 ≤ x ≤ 2 and 10 ≤ x ≤ 12.
Question
\(f(x)=1-\sqrt[3]{x}\)
(A) Find the intervals on which f is increasing or decreasing.
(B) Locate all maxima and minima.
(C) Find the intervals over which f is concave upward or downward.
(D) Find all inflection points.
(E) Sketch the graph of f.
▶️Answer/Explanation
(A)Use the first derivative to find where f is increasing or decreasing. The first derivative \(f'(x)=\frac{1}{3}x^{-\frac{2}{3}}< 0\) for (-∞, +∞), then f is decreasing for all values of x.
(B) First, find any points where f ′(x) = 0, but f ′ < 0 for all values of x. At x = 0, f ′(x) does not exist since there is a zero in the denominator. Therefore, there are no maxima or minima.
(C) Use the second derivative to test for concavity.\)f”(x)=\frac{2}{9}x^{-\frac{5}{3}}\).f”>0 when x > 0; therefore, f is concave upward on the interval (0, +∞). If x < 0, then f ″ < 0; therefore, f is concave downward on (-∞, 0).
(D) The second derivative f ″ changes concavity at x = 0, so there is an inflection point at x = 0. The function f (0) = 1, so the inflection point is at coordinate (0, 1), which is also the y-intercept.
(E) y-intercept at (0, 1). x-intercept at (1, 0).
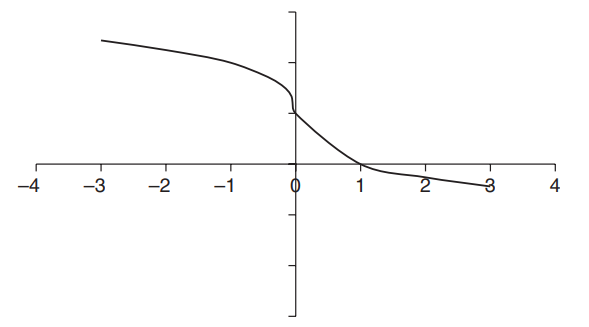
Question
Given the graph of f ′, find the following properties of the function f :
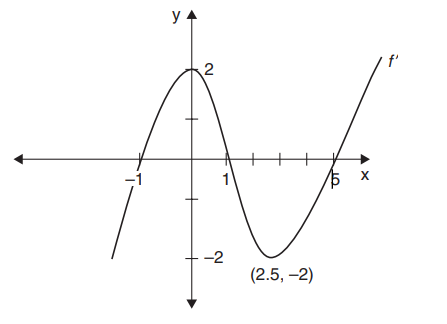
(A) The intervals on which f is increasing or decreasing
(B) The location of the relative maxima and minima
(C) The points of inflection and concavity of f
(D) Draw a sketch of f , given that f (-1) = f (1) = 5, f (0) = 0, and f (5) = -5.
▶️Answer/Explanation
(A) f ′ < 0 on (-∞, -1) and (1, 5), so f is decreasing. f ′ > 0 on (-1, 1) and (5, +∞), so f is increasing.
(B) The function has a relative maximum at x = 1 since f ′ changes from positive to negative. There are relative minima at x = (-1, 5) since f ′ changes from negative to positive.
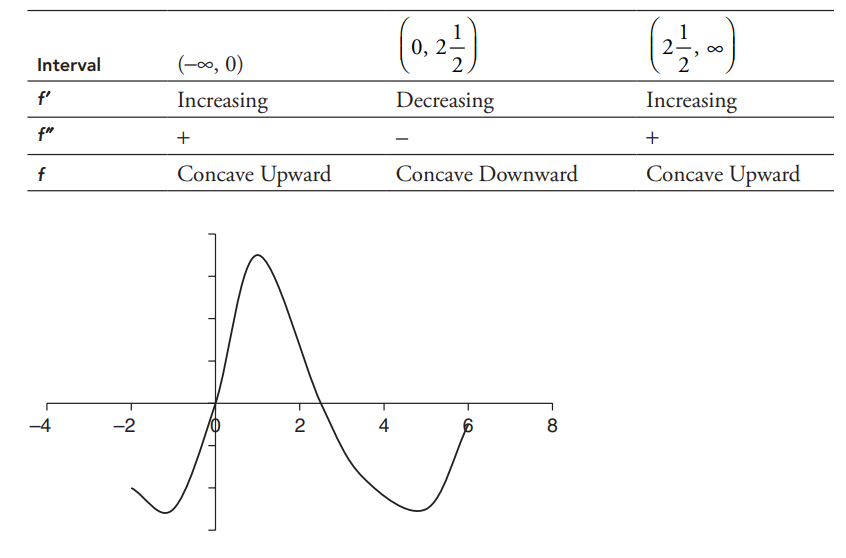
(C) f ′ is increasing on (-∞, 0), so f ′′ > 0 and f is concave upward. f ′ is decreasing on \(\left ( 0,2\frac{1}{2} \right )\) so f ′′ < 0 and f is concave downward. f ′ is increasing on\(\left ( 2\frac{1}{2} ,+\infty \right ) \), so f ′′ > 0 and f is concave upward. A change of concavity occurs at x = 0 and \(x=2\frac{1}{2}\) .Summarizing the results in a table:
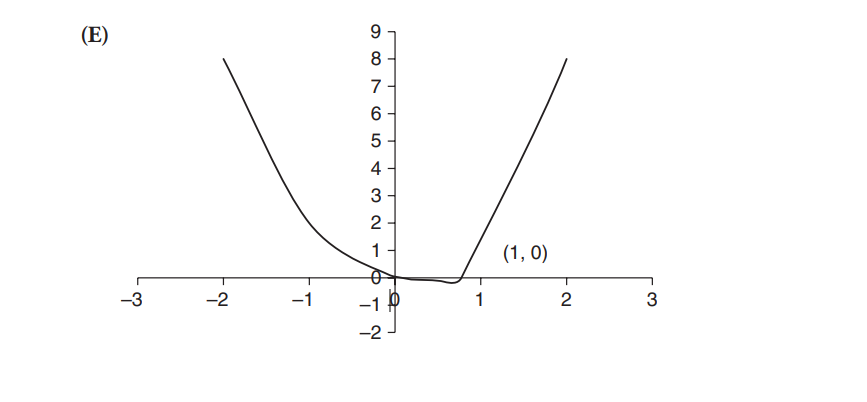
Question
\(f(x) =x^{4}-x^{3}\).
(A) Find the intervals on which f is increasing or decreasing.
(B) Locate all maxima and minima.
(C) Find the points of inflection, if any, on f .
(D) Find the intervals where f is concave upward or downward.
(E) Sketch the graph of \(f(x) =x^{4}-x^{3}\).
▶️Answer/Explanation
(A) To figure out where f (x) is increasing or decreasing, set \(f'(x)=4x^{3}-3x^{2}=x^{2}(4x-3)=0\)
The function equals zero at x = 0 and x = 3. Use a test point on each interval to find where f (x) is increasing or decreasing. The function f (x) is increasing on interval \(\left ( \frac{3}{4},\infty \right )\)
but is decreasing for interval (-∞, 0) and decreasing for \(\left ( 0,\frac{3}{4}\right )\).

B) You found in part (a) that f ′(x) = 0 at x = 0 and \(x=\frac{3}{4}\) . You then take the second derivative at those points to determine if they represent a maximum or minimum.You find that \(f{}”(x)=12x^{2}-6x\) You then substitute values for x to find that f ′′(0) = 0 and \(f”\left ( \frac{3}{4} \right )=\frac{9}{4}\). This demonstrates that \(f\left ( \frac{3}{4} \right )\) is a relative minimum. The test for f ′′(0) is inconclusive, so look back to the first derivative. The first derivative changes from positive to negative at x = 0, which implies that x = 0 is a relative maximum. At \(x=\frac{3}{4}\) ,f’=0 \(f”\left (\frac{3}{4}\right )=12\left ( \frac{9}{16} \right )-6\left ( \frac{3}{4} \right )=\frac{108}{16}-\frac{72}{16}=\frac{36}{16}> 0\) so \(\frac{3}{4}\) is a relative minimum.\(f\left ( \frac{3}{4} \right )=\left ( \frac{3}{4} \right )^{2}-\left ( \frac{3}{4} \right )^{4}-\left ( \frac{3}{4} \right )^{3}=\frac{81}{256}-\frac{108}{256}=-\frac{27}{256},\)so relative minimum at \(f\left ( \frac{3}{4} \right )=-\frac{27}{256}\).

Question
A curve is defined by the equation \(y=x^{3}-4\).
(A) Find the slope of the tangent to the curve at point (2, 4).
(B) Find the slope of the normal line at point (2, 4).
(C) Write an equation for the normal line.
▶️Answer/Explanation
(A) The slope of the tangent,\(m_{tangent}\), is defined as \(\frac{\mathrm{d} y}{\mathrm{d} x}.\frac{\mathrm{d} y}{\mathrm{d} x}=3x^{2}\).At \(x=2,\frac{\mathrm{d} y}{\mathrm{d} x}=12.\)
(B)\(m_{normal}=-\frac{1}{m_{tangent}}=-\frac{1}{3x^{2}}=-\frac{1}{12}\) at x=2.
(C) Since the slope of the normal line is \(-\frac{1}{12}\), if we take the point (2, 4), we can write \(\frac{y-4}{x-2}=-\frac{1}{12}\) or \(y=-\frac{1}{12}x+4\frac{1}{6}\).
Question
At time t, a particle moving in the xy-plane is at position ( x(t), y(t)), where x(t) and y(t) are not explicitly given. For t ≥ 0, \(\frac{dx}{dt}=4t + 1 and \frac{dy}{dt}= sin(t^{2}).\) At time t = 0, x(0) = 0 and y(0) = -4.
(a) Find the speed of the particle at time t = 3, and find the acceleration vector of the particle at time t = 3.
(b) Find the slope of the line tangent to the path of the particle at time t = 3.
(c) Find the position of the particle at time t = 3.
(d) Find the total distance traveled by the particle over the time interval 0 ≤ t ≤ 3.
▶️Answer/Explanation
Ans:
(a)
\(Speed =\sqrt{(\frac{dy}{dt})^{2}+(\frac{dx}{dt})^{2}}\)
\(\frac{dy}{dt}|_{t=3}=sin(3^{2})=sin9\)
\(\frac{dx}{dt}|_{t=3}=4(3)+1=13\)
\(Speed|_{t=3}=\sqrt{(sin9)^{2}+(13)^{2}}\)
Speed = 13.007
Acceleration Vector = \(\left \langle \frac{d^{2}x}{dt^{2}},{\frac{d^{2}y}{dt^{2}}} \right \rangle\)
\(\frac{dx}{dt}=4t +1; \frac{d^{2}x}{dt^{2}}=4\)
\(\frac{dy}{dt}=sin(t^{2}); \frac{d^{2}y}{dt^{2}}=2t cos (t^{2})\)
\(\frac{d^{2}x}{dt^{2}}|_{t=3}=4; \frac{d^{2}y}{dt^{2}}|_{t=3}=-5.467\)
Acceleration vector = <4, -5.467>
(b)
From part A,
\(\frac{dx}{dt}=\frac{\left ( \frac{dy}{dt} \right )}{\left ( \frac{dx}{dt} \right )}\) \(\frac{dy}{dt}|_{t=3}=sin9\)
\(\frac{dx}{dt}|_{t=3}=13\)
\(\frac{dy}{dx}= \frac{sin9}{13}=0.0317\)
(c)
x position at t = 3 is equal to x(0) + \(\int_{0}^{3}\frac{dx}{dt}dt\)
y position at t = 3 is equal to y(0) + \(\int_{0}^{3}\frac{dy}{dt}dt\)
\(x(3)=0+\int_{0}^{3}(4t+1)dt=21\)
\(y(3)=-4+\int_{0}^{3}sin(t^{2})dt=-3.226\)
At t = 3, the particle’s position is (21, -3.226)
(d)
Distance Travelled = \(\int_{0}^{3}\sqrt{\left ( \frac{dx}{dt} \right )^{2}+\left ( \frac{dy}{dt} \right )^{2}}dt\)
\(=\int_{0}^{3}\sqrt{(4t+1)^{2}+sin^{2}(t^{2})}dt\)
Distance Travelled = 21.091
Question
| x | 1 | 1.1 | 1.2 | 1.3 | 1.4 |
| f'(x) | 8 | 10 | 12 | 13 | 14.5 |
The function f is twice differentiable for x > 0 with f(1) = 15 and f”(1) = 20. Values of f’, the derivative of f, are given for selected values of x in the table above.
(a) Write an equation for the line tangent to the graph of f at x =1. Use this line to approximate f(1.4).
(b) Use a midpoint Riemann sum with two subintervals of equal length and values from the table to approximate \(\) Use the approximation for \(\) to estimate the value of f(1.4). Show
the computations that lead to your answer.
(c) Use Euler’s method, starting at x = 1 with two steps of equal size, to approximate f(1.4). Show the computations that lead to your answer.
(d) Write the second-degree Taylor polynomial for f about x = 1. Use the Taylor polynomial to approximate f(1.4).
▶️Answer/Explanation
Ans:
(a) f(1) = 15, f'(1) = 8
An equation for the tangent line is
y = 15 + 8 (x – 1) .
f(1.4) ≈ 15 + 8 (1.4 – 1) = 18.2
(b) \(\int_{1}^{1.4}f'(x)dx\approx (0.2)(10)+(0.2)(13)=4.6\)
\(f(1.4)=f(1)+\int_{1}^{1.4}f'(x)dx\)
f(1.4) ≈ 15 + 4.6 = 19.6
(c) f(1.2) ≈ f(1) + (0.2) (8) = 16.6
f(1.4) ≈ 16.6 + (0.2) (12) = 19.0
(d) \(T_{2}(x)=15+8(x-1)+\frac{20}{2!}(x-1)^{2}\)
= 15 + 8 (x-1) + 10(x – 1)2
f(1.4) ≈ 15 + 8(1.4-1) + 10(1.4 – 1)2 = 19.8
