Question:
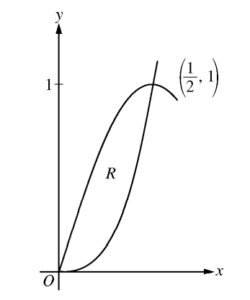
Let R be the region in the first quadrant enclosed by the graphs of f(x) = 8x3 and g(x) = sin(πx) , p as shown in the figure above.
(a) Write an equation for the line tangent to the graph of f at \(x = \frac{1}{2}.\)
(b) Find the area of R.
(c) Write, but do not evaluate, an integral expression for the volume of the solid generated when R is rotated about the horizontal line y = 1.
▶️Answer/Explanation
Ans:
(a)
f(x) = 8x3 \(f\left ( \frac{1}{2} \right ) = 8\left ( \frac{1}{8} \right )=1\) point of tangency : \(\left ( \frac{1}{2}, 1 \right )\)
f'(x) = 24x2 \(f’\left ( \frac{1}{2} \right )= 24 . \frac{1}{4}=6\)
y = 6x + b The tangent line to the graph of f
\(1 = 6\left ( \frac{1}{2} \right )+b\) at \(x = \frac{1}{2}\) is y = 6x-2.
1 = 3 + b
b = -2
y = 6x -2
(b)
f(x) = g(x)
8×3 = sin(πx)
x = 0 , \(\frac{1}{2}\)
\(R = \int_{0}^{\frac{1}{2}}\left [ 9(x)-f(x) \right ]dx = \int_{0}^{\frac{1}{2}}\left [ sin(\pi x)-8x^{3} \right ]dx=\frac{1}{\pi }\int_{0}^{\frac{1}{2}}sinu du – \int_{0}^{\frac{1}{2}}8x^{3}dx\)
\(= \frac{1}{\pi }(-cos(\pi x))_{0}^{\frac{1}{2}}-2x^{4}\) \(_{0}^{\frac{1}{2}}\)
\(= \frac{1}{\pi }(-cos(\frac{\pi }{2})+cos(01))-2\left ( \frac{1}{2} \right )^{4}+0\)
\(= \frac{1}{\pi }(1)-\frac{2}{16}\)
\(= \frac{1}{\pi }-\frac{1}{8}=\frac{8-\pi }{8\pi }\)
(c)
\(\pi \int_{0}^{\frac{1}{2}}\left [ \left ( 1-f(x) \right )^{2}-\left ( 1-9(x) \right )^{2} \right ]dx\)
Question:
At the beginning of 2010, a landfill contained 1400 tons of solid waste. The increasing function W models the total amount of solid waste stored at the landfill. Planners estimate that W will satisfy the differential equation \(\frac{dW}{dt}=\frac{1}{25}(W-300)\) for the next 20 years. W is measured in tons, and t is measured in years from the start of 2010.
(a) Use the line tangent to the graph of W at t = 0 to approximate the amount of solid waste that the landfill contains at the end of the first 3 months of 2010 \(\left ( time t = \frac{1}{4} \right )\).
(b) Find \(\frac{d^{2}W}{dt^{2}}\) in terms of W. Use \(\frac{d^{2}W}{dt^{2}}\) to determine whether your answer in part (a) is an underestimate or an overestimate of the amount of solid waste that the landfill contains at time \(t = \frac{1}{4}\).
(c) Find the particular solution W = W(t) to the differential equation \(\frac{dW}{dt}=\frac{1}{25}(W-300)\) with initial condition W(0) = 1400.
▶️Answer/Explanation
Ans:
(a)
at t = 0, W = 1400
so
\(\frac{dW}{dt}|_{t=0} = \frac{1}{25}(1100)=44 tons/ year = W'(0)\)
W(x + a) ≈ W(λ) + aW'(x)
\(W\left ( 0+\frac{1}{4} \right )\approx W(0)+\frac{1}{4}W'(0)\)
\(W\left ( \frac{1}{4} \right )\approx 1400 + 11\)
\(W\left ( \frac{1}{4} \right )\approx 1411 tons\)
There will be about 1411 tons of landfill after 3 months.
(b)
\(\frac{dW}{dt}=\frac{1}{25}W-12\)
\(\frac{d^{2}W}{dt^{2}}=\frac{1}{25}\frac{dW}{dt}\)
\(\frac{d^{2}W}{dt^{2}}=\frac{1}{625}(W-300)\)
so \(\frac{d^{2}W}{dt^{2}}\) is always positive
b/c W > 300.
The answer in part a is an under estimate because since \(\frac{d^{2}W}{dt^{2}}\) is always positive for t > 0, the graph of W is concave up, so the linearization of W is an underestimate.
(c)
\(\frac{dW}{dt}=\frac{1}{25}(W-300)\)
\(\int \frac{dw}{W-300}=\int \frac{1}{25}dt\)
\(e^{\xi n}\left | W-300 \right |=\frac{1}{25}t+c\)
can remove abs value
b/c W > 300. (iner fn)
[W – 300] = (e 1/25 t
Initial condition w(0) = 1400
1400-300 = C e0
1100 = C
W – 300 = 1100 e 1/25 t
W = W(t) = 1100 e 1/25 t + 300
Question:
The rate at which a baby bird gains weight is proportional to the difference between its adult weight and its current weight. At time t = 0, when the bird is first weighed, its weight is 20 grams. If B (t) is the weight of the bird, in grams, at time t days after it is first weighed, then
\(\frac{dB}{dt}= \frac{1}{5}(100-B).\)
Let y = B (t) be the solution to the differential equation above with initial condition B(0) = 20.
(a) Is the bird gaining weight faster when it weighs 40 grams or when it weighs 70 grams? Explain your reasoning.
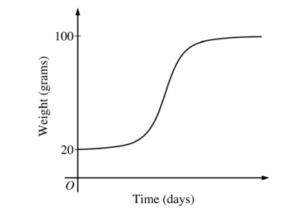
(b) Find \(\frac{d^{2}B}{dt^{2}}\) in terms of B. Use \(\frac{d^{2}B}{dt^{2}}\) to explain why the graph of B cannot resemble the following graph.
(c) Use separation of variables to find y = B(t), the particular solution to the differential equation with initial condition B(0) = 20.
▶️Answer/Explanation
Ans:
(a) When it is 40 grams : \(\frac{dB}{dt}=\frac{1}{5}(100-40)=12\) g/day
when it is 70 grams: \(\frac{dB}{dt}=\frac{1}{5}(100-70)=6\) g/day
So the bird is gaining weight faster when it weighs 40 grams.
(b)
\(\frac{dB}{dt}=20-\frac{1}{5}B\)
\(\frac{d^{2}B}{dt^{2}}=-\frac{1}{5}.\frac{dB}{dt}\)
\(=-\frac{1}{5}(20-\frac{1}{5}B)\)
\(=\frac{1}{25}B-4\)
\(\frac{1}{25}B-4>0\)
B > 100
So, the graph cannot be concave up when weight is below 100 g.
(c)
\(\frac{dB}{dt}=\frac{1}{5}(100-B)\)
\(\frac{1}{\frac{1}{5}(100-B)}dB = dt\)
\(\frac{1}{100-B}dB = dt\)
\(\int \frac{1}{100-B}dB = \int 1dt\)
-5 In [100-B] = t + c
\(In (100-B) = – \frac{1}{5}(t+c)\)
\(100-B = e^{- \frac{1}{5}(t+c)}\)
\(B = 100-e^{- \frac{1}{5}(t+c)}\)
\(20 = 100-e^{- \frac{1}{5}c}\)
\(e^{- \frac{1}{5}c}=80\)
\(- \frac{1}{5}c= ln 80\)
\(c = -5 ln 80\)
\(\partial B= 100-e^{- \frac{1}{5}c+-5 ln 80}\)
Question:
Consider the differential equation \(\frac{dy}{dx}=2x – y.\)
(a) On the axes provided, sketch a slope field for the given differential equation at the six points indicated.
(b) Find \(\frac{d^{2}y}{dx^{2}}\) in terms of x and y. Determine the concavity of all solution curves for the given differential equation in Quadrant II. Give a reason for your answer.
(c) Let y = f(x) be the particular solution to the differential equation with the initial condition f (2) = 3.
Does f have a relative minimum, a relative maximum, or neither at x = 2 ? Justify your answer.
(d) Find the values of the constants m and b for which y = mx + b is a solution to the differential equation.
▶️Answer/Explanation
Ans:
(b)
\(\frac{dy}{dx}= 2x – y\)
\(\frac{d^{2}y}{dx^{2}}= 2-\frac{dy}{dx}=2-(2x-y)\)
\(\frac{d^{2}y}{dx^{2}}= 2-2x+y\)
In Quadrant II, x < 0 and y > 0, So \(\frac{d^{2}y}{dx^{2}}= 2-2x+y>0,\)
Thus all solution curves in Quadrant II are concave up.
(c)
\(\frac{dy}{dx}= 2x-y=2.2-3 =1\)
Neither, as \(\frac{dy}{dx}\) ≠ 0 at x = 2.
(d)
\(\frac{dy}{dx}= 2x-y\), y = mx + b
\(\frac{dy}{dx}= m = 2x – y\)
m = 2x – (mx + b)
m = (2-m)x – b, equate coefficients
2 – m = 0
m = 2
-b = m
b = -m = -2.
m = 2, b = -2
Question:
Consider the curve given by the equation y3 – xy = 2. It can be shown that \(\frac{dy}{dx}= \frac{y}{3y^{2}-x}.\)
(a) Write an equation for the line tangent to the curve at the point (-1, 1).
(b) Find the coordinates of all points on the curve at which the line tangent to the curve at that point is vertical.
(c) Evaluate \(\frac{d^{2}y}{dx^{2}}\) at the point on the curve where x = -1 and y = 1.
▶️Answer/Explanation
Ans:
(a)
\(Slope = \frac{dy}{dx}@(-1, 1): \frac{1}{3(1)^{2}-(-1)}=\frac{1}{4}\)
Point = ( -1, 1)
\(y – 1 = \frac{1}{4}(x+1)\)
\(y – 1 = \frac{x}{4}+\frac{1}{4}\)
\(y = \frac{x}{4}\times +\frac{5}{4}\)
(b) Vertical tangent line ⇒ slope undefined
⇒ denominator = 0 ⇒ 3y2 – x = 0
3y2 = x
Substitute “x” for “3y2” in the equation of the curve
\(y ^{3}-\left [ 3y^{2}\cdot y \right ]= 2\) y3 – 3y2 = 2
-2y3 = 2
(-1)3 – x•(-1) = 2 Vertical tangents y3 = -1
-1 + x = 2 at (3, 1) y = -1
x = 3
(c)
\(\frac{dy}{dx}@(-1, 1)=\frac{1}{4}\) 3y2 – x = 3-(-1) = 4
\(\frac{d^{2}y}{dx^{2}}=\frac{\left [ y’\cdot (3y^{2}-x) \right ]-\left [ (6yy’ -1)\cdot (y) \right ]}{\left ( 3y^{2}-x \right )^{2}}\)
\(= \frac{\left ( \frac{1}{4}\cdot 4 \right )-\left ( \frac{1}{2}\cdot 1 \right )}{16}=\frac{1-\frac{1}{2}}{16}=\frac{\frac{1}{2}}{16}=\frac{1}{2}\cdot \frac{1}{16}\)
\(=\frac{1}{32}\)
Question:
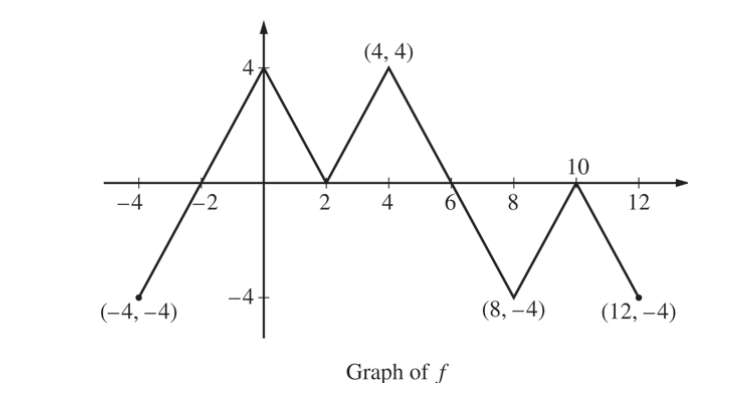
The figure above shows the graph of the piecewise-linear function f. For -4 ≤ x ≤ 12, the function g is defined by\(g(x)=\int_{2}^{x}f(t)dt.\)
(a) Does g have a relative minimum, a relative maximum, or neither at x = 10 ? Justify your answer.
(b) Does the graph of g have a point of inflection at x = 4 ? Justify your answer.
(c) Find the absolute minimum value and the absolute maximum value of g on the interval -4 ≤ x ≤ 12. Justify your answers.
(d) For -4 ≤ x ≤ 12 , find all intervals for which g (x) ≤ 0.
▶️Answer/Explanation
Ans:
(a)
g'(x) = f(x)
g does not have a relative minimum or maximum at x = 10 because g'(x) = f(x) does not change sign at this point.
(b)
g”(x) = f'(x)
f'(x) = g”(x) does change sign at x = 4 so g does have a point of inflection at this point
(c)
g'(x) = f(x) = 0 x = -2 x = 2
x = 6 x = 10
does not change sign at x = 2 and x = 10
The absolute minimum value of g on the interval -4 ≤ x ≤ 12 is -8 and the absolute maximum value of g is 8.
(d)
\(g(x)=\int_{2}^{x}f(t)dt\leq 0\)
g(x) = 0 at x = 2 and x = 10
g(x) ≤ 0 in the intervals -4 ≤ x ≤ 2 and 10 ≤ x ≤ 12
Question:
At time t = 0, a boiled potato is taken from a pot on a stove and left to cool in a kitchen. The internal temperature of the potato is 91 degrees Celsius (°C) at time t = 0, and the internal temperature of the potato is greater than 27 C° for all times t > 0. The internal temperature of the potato at time t minutes can be modeled by the function H that satisfies the differential equation \(\frac{dH}{dt}=-\frac{1}{4}(H-27)\), where H(t) is measured in degrees Celsius and H( 0) = 91 .
(a) Write an equation for the line tangent to the graph of H at t = 0. Use this equation to approximate the internal temperature of the potato at time t = 3.
(b) Use \(\frac{d^{2}H}{dt^{2}}\) to determine whether your answer in part (a) is an underestimate or an overestimate of the internal temperature of the potato at time t = 3.
(c) For t < 10, an alternate model for the internal temperature of the potato at time t minutes is the function G that satisfies the differential equation \(\frac{dG}{dt} = -(G-27)^{2/3},\) where G(t) is measured in degrees Celsius and G(0) = 91. Find an expression for G (t). Based on this model, what is the internal temperature of the potato at time t = 3 ?
▶️Answer/Explanation
Ans:
(a)
\(\frac{dH}{dt}_{H=91} = -\frac{1}{4}(91-27)=\left ( -\frac{1}{4} \right )(64)=-16\)
A(t) = -16 (t-0) + 91
A(t) = -16t + 91
A(3) = – 16(3) + 91
= -48 + 91
430C
at t = 3 minutes
(b)
\(\frac{dH}{dt} = -\frac{1}{4}(H-27)\) H > 27 for all t > 0
\(\frac{d^{2}H}{dt^{2}} = -\frac{1}{4}\left ( \frac{dH}{dt} \right )\) \(\frac{d^{2}H}{dt^{2}}\) is always positive,
\(-\frac{1}{4}\left ( -\frac{1}{4} \right )(H-24)\) So part (a) is an underestimate.
\(\frac{d^{2}H}{dt^{2}} = \frac{1}{16}(H-24)\)
(c)
\(\frac{dG}{dt} = -(G-27)^{2/3}\)
\(\int \frac{dG}{(G-27)^{2/3}}=\int -1dt\)
\(\int (G-27)^{-2/3}dt = -t+c\)
3 (G-27) 1/3 = -t + c1
\((G-27)^{-2/3} = -\frac{t}{3}+c_{2}\)
\(G-27 = \left ( -\frac{t}{3}+c_{2} \right )^{3}\)
\(G = \left ( -\frac{t}{3}+c_{2} \right )^{3}+27\)
at (0, 91)
\(91= (0+c_{2})^{3}+27\)
91 = (c2)3 + 27
64 = (c2)3 →c2 = 4
\(G(t)= \left ( -\frac{t}{3}+4 \right )^{3}+27\)
\(G(3)= \left ( \frac{-3}{3}+4 \right )^{3}+27\)
= (3)3 + 27
= 27 + 27
G(3) = 540C
Question:
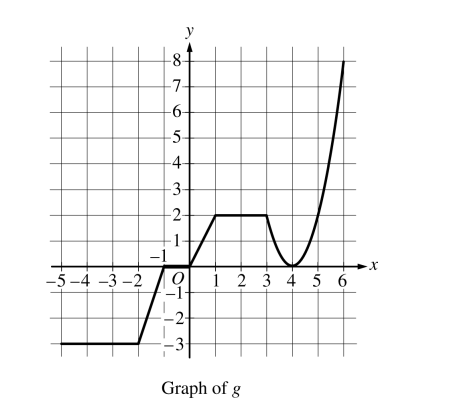
The graph of the continuous function g, the derivative of the function f, is shown above. The function g is piecewise linear for − 5 ≤ x ≤ 3 , and g(x) = 2 ( x− 4)2 for 3 ≤ x ≤ 6.
(a) If f (1) = 3, what is the value of f (−5) ?
(b) Evaluate \(\int_{1}^{6}g(x)dx\) .
(c) For − 5 ≤ x ≤ 6, on what open intervals, if any, is the graph of f both increasing and concave up? Give a reason for your answer.
(d) Find the x-coordinate of each point of inflection of the graph of f. Give a reason for your answer.
▶️Answer/Explanation
Ans:
(a)
f'(x) = g(x)
\(f(x)=\int_{1}^{x}g(t)dt+3\)
\(f(-5)=-\int_{-5}^{1}g(t)dt+3\)
\(f(-5)=-\left ( \frac{1}{2} (1)(2)-\frac{1}{2} (1)(3)-(3)(3)\right )+3\)
\(f(-5)=-\left ( 1-\frac{3}{2}-9\right )+3\)
\(f(-5)=8+\frac{3}{2}+3\)
\(f(-5)=11+\frac{3}{2}\)
(b)
\(\int_{1}^{6}g(x)dx=\int_{1}^{3}g(x)dx+\int_{3}^{6}g(x)dx\)
\(\int_{1}^{6}g(x)dx=(2)(2)+\int_{3}^{6}2(x-4)^{2}dx\)
\(\int_{1}^{6}g(x)dx=4+\left ( \frac{2}{3}(x-4)^{3} \right )|_{3}^{6}\)
\(\int_{1}^{6}g(x)dx=4+\left ( \frac{2}{3}(8)- \frac{2}{3}(-1)\right )\)
\(\int_{1}^{6}g(x)dx=4+\frac{16}{3}+\frac{2}{3}\)
\(\int_{1}^{6}g(x)dx=10\)
(c)
On the interval (0, 1) u(4, 6) f is both increasing and concave up since f'(x) = g(x) and g is positive on the that interval meaning f is increasing on that interval, and g is increasing on that interval, meaning f”(x)>0 on that interval, therefore f is concave up on that interval
(d)
f has a point of inflection at x = 4 since f'(x) = g(x) and since a switches from decreasing to increasing at x = 4, therefore f”(x) = 0 at that point and would change signs from (-) to (+) at x = 4, therefore x = 4 is an inflection point.
Question:
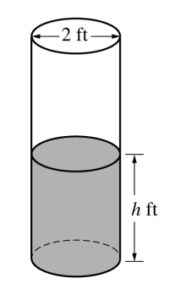
A cylindrical barrel with a diameter of 2 feet contains collected rainwater, as shown in the figure above. The water drains out through a valve (not shown) at the bottom of the barrel. The rate of change of the height h of the water in the barrel with respect to time t is modeled by \(\frac{dh}{dt}=-\frac{1}{10}\sqrt{h},\) where h is measured in feet and t is measured in seconds. (The volume V of a cylinder with radius r and height h is V = πr2h.)
(a) Find the rate of change of the volume of water in the barrel with respect to time when the height of the water is 4 feet. Indicate units of measure.
(b) When the height of the water is 3 feet, is the rate of change of the height of the water with respect to time increasing or decreasing? Explain your reasoning.
(c) At time t = 0 seconds, the height of the water is 5 feet. Use separation of variables to find an expression for h in terms of t.
▶️Answer/Explanation
Ans:
(a)
h = 4
\(\frac{dh}{dt}=\frac{-1}{10}\sqrt{4}=\frac{-1}{5}\) \(\frac{dv}{dt}=\pi \left [ r^{2}\frac{dh}{dt}+h(2r)\left ( \frac{dr}{dt} \right ) \right ]\)
\(\frac{dv}{dt}=?\) \(\frac{dv}{dt}=\pi \left [ (1)\left ( \frac{-1}{5} \right )+(4)(2)(0) \right ]\)
r = 1
\(\frac{dv}{dt}=0\) \(\frac{dv}{dt}=\frac{-\pi }{5}ft^{3}/sec\)
(b)
h = 3
\(\frac{d^{2}h}{dt^{2}}=?\) \(\frac{d^{2}h}{dt^{2}}=\frac{-1}{20}h^{-1/2}\frac{dh}{dt}=\frac{-1}{20\sqrt{3}}\left ( \frac{-1}{10}\sqrt{3} \right )=\frac{1}{200}\)
\(\frac{-1}{10}h^{1/2}\) The rate of change of height is increasing since \(\frac{d^{2}h}{dt^{2}}\) at h = 3 is positive.
1/20
(c)
\(\int h^{-1/2}dh=\int \frac{-1}{10}dt\)
\(\int h^{1/2}=\frac{-1}{10}t+c_{1}\)
\(h^{1/2}=\frac{-1}{20}t+c_{2}\)
\(h=\left ( \frac{-1}{20}t+c \right )^{2}\)
\(5=\left ( \frac{-1}{20}(0)+c \right )^{2}\)
\(c = \sqrt{5}\)
\(h = \left ( \frac{-1}{20}t+\sqrt{5} \right )^{2}\)
Question
Let g(x )=\(xe^{-x}+be^{-x}\), where b is a positive constant.
(a) Find\( \lim_{x\rightarrow \infty }g(x)\)
(b) For what positive value of b does g have an absolute maximum at \(x=\frac{2}{3}\)? Justify your answer.
▶️Answer/Explanation
(c) Find all values of b, if any, for which the graph of g has a point of inflection on the interval \(0 < x <\infty\). Justify your answer.
(a)\(\lim_{x\rightarrow \infty }g(x)=0\)
(b)\(g'(x)=e^{-x}-xe^{-x}-be^{-x}=(1-x-b)e^{-x}\)
\(g’\left ( \frac{2}{3} \right )=\left ( \frac{1}{3}-b \right )e^{2/3}=0\Rightarrow b=\frac{1}{3}\)when \(b=\frac{1}{3},g'(x)=\left ( \frac{2}{3}-x \right )e^{-x}\)
for\(x<\frac{2}{3},g'(x)>0 \) and for\( x>\frac{2}{3},g'(x)<0\) Therefore, when\( b =\frac{1}{3}\),g has an absolute maximum at \(x=\frac{2}{3}.(c) g”(x) = −e^{-x} (1 − x – b)e^{-x} ̄= (x −2+b)e^{-x} ̄\)
If\( 0 <b< 2, then g”(x) \)will change sign at x = 2 − b > 0. Therefore, the graph of g will have a point of inflection on the interval 0 < x < ∞ when 0 < b < 2.
