Question
The function \(f\) is twice differentiable with \(f(2)=1, f^{\prime}(2)=4\), and \(f^{”}(2)=3\). What is the value of the approximation of \(f(1.9)\) using the line tangent to the graph of \(f\) at \(x=2\) ?
A 0.4
B 0.6
C 0.7
D 1.3
E 1.4
▶️Answer/Explanation
Ans:B
\[
f(2)=1, f^{\prime}(2)=4 f^{\prime \prime}(2)=3 x=2 f(1.9)=?
\]
The formula for the slope of a tangent line to a curve \(y=f(x)\) at the point \((a, f(a))\) is:
\[
\begin{aligned}
m & =\frac{y-f(a)}{x-a} \\
f^{\prime}(a) & =\frac{y-f(a)}{x-a}
\end{aligned}
\]
Rewrite the above expression for the variable \(y\) or the function \(f(x)\).
\[
\begin{aligned}
(x-a) f^{\prime}(a) & =y-f(a) \\
y-f(a) & =(x-a) f^{\prime}(a) \\
y & =(x-a) f^{\prime}(a)+f(a) \\
f(x) & =(x-a) f^{\prime}(a)+f(a) \quad[\because y=f(x)]
\end{aligned}
\]
Substitute \(a=2\) in the above function.
\[
\begin{array}{rlr}
f(x) & =(x-2) f^{\prime}(2)+f(2) & \\
& =(x-2) 4+1 \quad\left[\because f^{\prime}(2)=4 \text { and } f(2)=1\right] \\
& =4 x-8+1 \\
& =4 x-7
\end{array}
\]
Substitute \(x=1.9\) in the above function and solve for
\[
\begin{aligned}
& f(1.9) . \\
& \begin{aligned}
f(1.9) & =4(1.9)-7 \\
& =7.6-7 \\
& =0.6
\end{aligned}
\end{aligned}
\]
Question
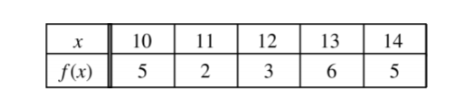
The table above gives values of the continuous function f at selected values of x. If f has exactly two critical points on the open interval (10, 14) , which of the following must be true?
A f(x) > 0 for all x in the open interval (10, 14)
B f‘(x) exists for all x in the open interval (10, 14)
C f‘(x) < 0 for all x in the open interval (10, 11)
D f‘(12) ≠ 0
▶️Answer/Explanation
Ans:D
Question
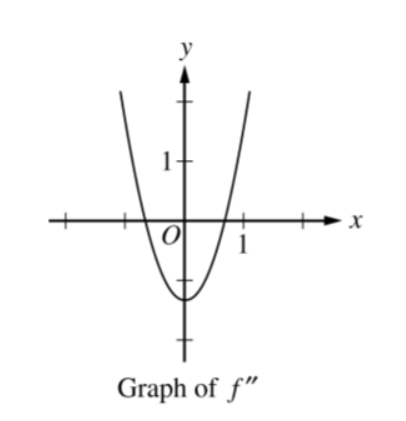
The graph of f”,the second derivative of the function f, is shown above. Which of the following could be the graph of f ?
A 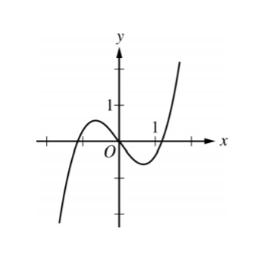
B 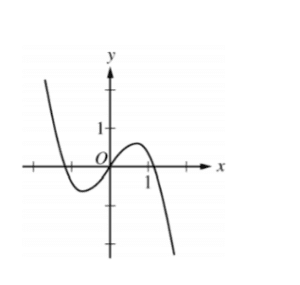
C 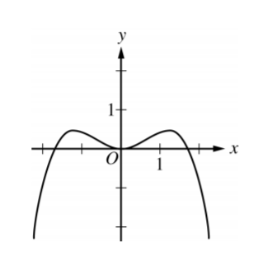
D 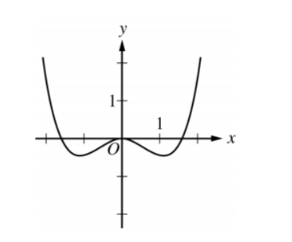
▶️Answer/Explanation
Ans:D
Question
The graph of f’, the derivative of the function f, is shown in the figure above. Which of the following statements must be true?
I. f is continuous on the open interval (a, b).
II f is decreasing on the open interval (a, b).
III The graph of f is concave down on the open interval (a, b).
A I only
B I and II only
C I and III only
D II and III only
▶️Answer/Explanation
Ans:C
Question
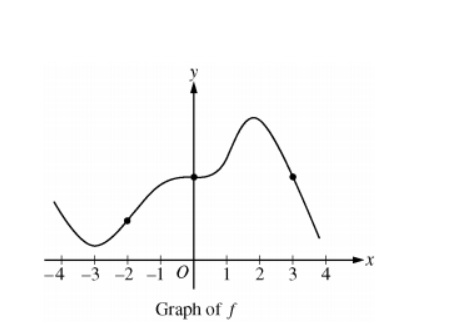
The graph of a differentiable function f is shown in the figure above. Which of the following is true?
A f′(−2)<f′(0)<f′(3)
B f′(−2)<f′(3)<f′(0)
C f′(3)<f′(−2)<f′(0)
D f′(3)<f′(0)<f′(−2)
▶️Answer/Explanation
Ans:D
