Question:
On a certain workday, the rate, in tons per hour, at which unprocessed gravel arrives at a gravel processing plant is modeled by \(G(t)=90+45 Cos\left ( \frac{t^{2}}{18} \right ),\) where t is measured in hours and 0 ≤ t ≤ 8. At the beginning of the workday (t = 0), the plant has 500 tons of unprocessed gravel. During the hours of operation,0 ≤ t ≤ 8 the plant processes gravel at a constant rate of 100 tons per hour.
(a) Find G’(5). Using correct units, interpret your answer in the context of the problem.
(b) Find the total amount of unprocessed gravel that arrives at the plant during the hours of operation on this workday.
(c) Is the amount of unprocessed gravel at the plant increasing or decreasing at time t = 5 hours? Show the work that leads to your answer.
(d) What is the maximum amount of unprocessed gravel at the plant during the hours of operation on this workday? Justify your answer.
▶️Answer/Explanation
Ans:
(a)
\(G(t)=90+45 Cos\frac{t^{2}}{18}\)
\(G'(t)=-5t sin\left ( \frac{t^{2}}{18} \right )\)
G’(5) = – 24.588 tons/ hr2
This means that the rate at which unprocessed gravel arrives at the processing plant is changing by -24.588 tons per hour per hour, or decreasing by 24.588 tons per hour per hour, at t = 5 hours.
(b)
\(\int_{0}^{8}\left [ 90+45 cos\left ( \frac{t^{2}}{18} \right ) \right ]dt= 825.551 tons\)
(c)
Let V(t) be the amount of unprocessed gravel.
V’(t) is the rate of which the amount of unprocessed gravel is changing.
V’(t) = G(t) – 100
V’(5) = G(5) – 100
\(=90+45 cos \left ( \frac{52}{18} \right )-100\)
V’(5) = – 1.859
Since V’(5) is negative the amount of unprocessed gravel is decreasing at time t = 5 hours
(d)
V’(t) = 0 at t = ?
0 = G(t) – 100
\(100=90+45 cos \left ( \frac{t^{2}}{18} \right )\)
\(10=45 cos \left ( \frac{t^{2}}{18} \right )\)
T = 4.923
\(v(t)-v(0)=\int_{0}^{t}\left ( G(x)-100 \right )dx\)
\(v(t)=\int_{0}^{t}\left ( G(x)-100 \right )dx+v(0)\)
V (0) = 500
V(4.923) = 635.76
V(8) = 525.551
Since v(t) is on a closed interval [0, 8 ], the maximum amount must occur at an endpoint or at a critical value after evaluating the amount of unprocessed gravel at t = 0, t = 4.923, and t = 8, the amount of unprocessed gravel is highest at t = 4.923, with 635.376 tons of unprocessed gravel.
Question
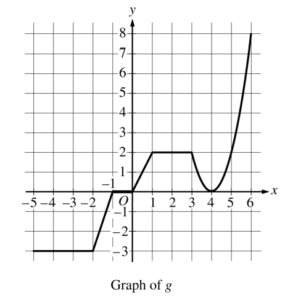
The graph of the continuous function g, the derivative of the function f, is shown above. The function g is piecewise linear for −5 ≤ x < 3, and g (x) = 2(x −4 ) 2 for 3 ≤ x ≤ 6.
(a) If f (1) = 3, what is the value of f(−5) ?
(b) Evaluate \(\int_{1}^{6}g(x)dx.\)
(c) For −5 < x < 6, on what open intervals, if any, is the graph of f both increasing and concave up? Give a reason for your answer.
(d) Find the x-coordinate of each point of inflection of the graph of f. Give a reason for your answer.
▶️Answer/Explanation
Ans:
(a) \(f(-5)=f(1)+\int_{1}^{-5}g(x)dx=f(1)-\int_{-5}^{1}g(x)dx\)
\(=3-\left ( -9-\frac{3}{2}+1 \right )=3-\left ( -\frac{19}{2} \right )=\frac{25}{2}\)
(b) \(\int_{1}^{6}g(x)dx=\int_{1}^{3}g(x)dx+\int_{3}^{6}g(x)dx\)
\(=\int_{1}^{3}2dx+\int_{3}^{6}2(x-4)^{2}dx\)
\(=4+_{x=3}\left [ \frac{2}{3}(x-4)^{3} \right ]^{x=6}=4+\frac{16}{3}-\left ( -\frac{2}{3} \right )=10\)
(c) The graph of f is increasing and concave up on 0 < x < 1 and 4 < x < 6 because f ‘(x) =g(x)> 0 and f ‘(x) = g(x) is increasing on those intervals.
(d) The graph of f has a point of inflection at x = 4 because f'(x) = g(x) changes from decreasing to increasing at x = 4.
