Question:

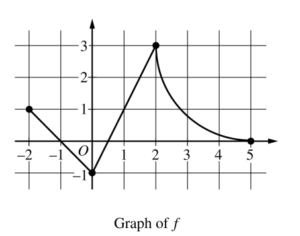
The function f is defined on the closed interval [-5, 4] . The graph of f consists of three line segments and is shown in the figure above. Let g be the function defined by \(g(x)=\int_{-3}^{x}f(t)dt.\)
(a) Find g(3) .
(b) On what open intervals contained in -5 < x < 4 is the graph of g both increasing and concave down? Give a reason for your answer.
(c) The function h is defined by \(h(x)= \frac{g(x)}{5x}\). Find h'(3).
(d) The function p is defined by p(x) = f(x2 – x). Find the slope of the line tangent to the graph of p at the point where x = -1.
▶️Answer/Explanation
Ans:
\(g(x)= \int_{-3}^{3}f(t)dt\)
\(= \frac{1}{2}(5)(4)-\frac{1}{2}(1)(2)\)
= 10 – 1 = 9
(b)
g'(x) > 0 ⇔ f(x) > 0
g”(x) < 0 ⇔ f'(x) < 0
(-5, -3), (0, 2)
(c)
\(h(x)=\frac{g(x)}{5x}\)
\(h'(x)= \frac{(5x)(g'(x))-g(x).5}{25x^{2}}\)
\(h'(3)= \frac{(15)(f(3))-g(3).5}{9.25}=\frac{(15)(-2)-(9)(5)}{9.25}\)
(d)
p(x) = f(x2 – x)
p'(x) = f'(x2-x) . (2x-1)
p'(-1) = f'(1+1) . (-2-1) = f'(2).-3
= (-2) (-3)
= 6
\({f}'(2)=\frac{-4-4}{4-0}=\frac{-8}{4}=-2\)
Question:
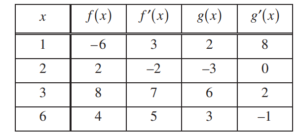
The functions f and g have continuous second derivatives. The table above gives values of the functions and their derivatives at selected values of x.
(a) Let k(x) = f(g(x)). Write an equation for the line tangent to the graph of k at x = 3.
(b) Let \(h(x)=\frac{g(x)}{f(x)}.\) Find h'(1).
(c) Evaluate \(\int_{1}^{3}f”(2x)dx.\)
▶️Answer/Explanation
Ans:
(a)
K(3) = f(g(3))
= f(6)
= 4
k'(x) = f'(g(x)) ·g'(x)
k'(3) = f'(g(3))·g'(3)
= f'(6)·2
= 5.2
= 10
y – 4 = 10 (x-3)
(b)
\(h'(x)=\frac{f(x)g'(x)-g(x)f'(x)}{(f(x))^{2}}\) \(h'(1)=\frac{-2}{2}\)
\(h'(1)=\frac{f(1)g'(1)-g(1)f'(1)}{(f(1))^{2}}\)
\(=\frac{(-6)(8)-(2)(3)}{(-6)^{2}}\)
\(=\frac{-48-6}{36}\)
\(=\frac{-54}{36}\)
(c)
\(\left [ \frac{1}{2}f'(2x) \right ]_{1}^{3}\)
\(\left [ \frac{1}{2}f'(6) \right ]-\left [ \frac{1}{2}f'(2) \right ]\)
\(\frac{5}{2}+1\)
\(\frac{7}{2}\)
Question:
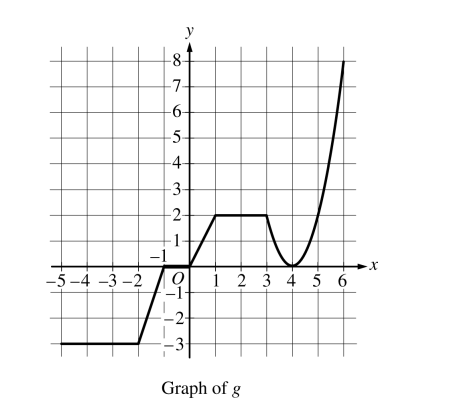
The graph of the continuous function g, the derivative of the function f, is shown above. The function g is piecewise linear for − 5 ≤ x ≤ 3 , and g(x) = 2 ( x− 4)2 for 3 ≤ x ≤ 6.
(a) If f (1) = 3, what is the value of f (−5) ?
(b) Evaluate \(\int_{1}^{6}g(x)dx\) .
(c) For − 5 ≤ x ≤ 6, on what open intervals, if any, is the graph of f both increasing and concave up? Give a reason for your answer.
(d) Find the x-coordinate of each point of inflection of the graph of f. Give a reason for your answer.
▶️Answer/Explanation
Ans:
(a)
f'(x) = g(x)
\(f(x)=\int_{1}^{x}g(t)dt+3\)
\(f(-5)=-\int_{-5}^{1}g(t)dt+3\)
\(f(-5)=-\left ( \frac{1}{2} (1)(2)-\frac{1}{2} (1)(3)-(3)(3)\right )+3\)
\(f(-5)=-\left ( 1-\frac{3}{2}-9\right )+3\)
\(f(-5)=8+\frac{3}{2}+3\)
\(f(-5)=11+\frac{3}{2}\)
(b)
\(\int_{1}^{6}g(x)dx=\int_{1}^{3}g(x)dx+\int_{3}^{6}g(x)dx\)
\(\int_{1}^{6}g(x)dx=(2)(2)+\int_{3}^{6}2(x-4)^{2}dx\)
\(\int_{1}^{6}g(x)dx=4+\left ( \frac{2}{3}(x-4)^{3} \right )|_{3}^{6}\)
\(\int_{1}^{6}g(x)dx=4+\left ( \frac{2}{3}(8)- \frac{2}{3}(-1)\right )\)
\(\int_{1}^{6}g(x)dx=4+\frac{16}{3}+\frac{2}{3}\)
\(\int_{1}^{6}g(x)dx=10\)
(c)
On the interval (0, 1) u(4, 6) f is both increasing and concave up since f'(x) = g(x) and g is positive on the that interval meaning f is increasing on that interval, and g is increasing on that interval, meaning f”(x)>0 on that interval, therefore f is concave up on that interval
(d)
f has a point of inflection at x = 4 since f'(x) = g(x) and since a switches from decreasing to increasing at x = 4, therefore f”(x) = 0 at that point and would change signs from (-) to (+) at x = 4, therefore x = 4 is an inflection point.
Question:
The continuous function f is defined on the closed interval −6 ≤ x ≤ 5. The figure above shows a portion of the graph of f, consisting of two line segments and a quarter of a circle centered at the point (5, 3). It is known that the point \((3,3-\sqrt{5})\) is on the graph of f.
(a) If \(\int_{-6}^{5}f(x)dx=7,\) find the value of \(\int_{-6}^{-2}f(x)dx.\) Show the work that leads to your answer
(b) Evaluate \(\int_{3}^{5}(2f'(x)+4)dx.\)
(c) The function g is given by \(g(x)=\int_{-2}^{x}f(t)dt.\) Find the absolute maximum value of g on the interval − 2 ≤ x ≤ 5. Justify your answer.
(d) Find \(\lim_{x\rightarrow 1}\frac{10^{x}-3f'(x)}{f(x)-arctan x}.\)
▶️Answer/Explanation
Ans:
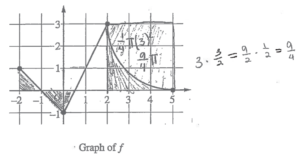
(a)
\(\int_{-6}^{-2}f(x)dx=\int_{-6}^{5}f(x)dx-\int_{-2}^{5}f(x)dx\)
\(\int_{-6}^{-2}f(x)dx=7-\left [ \frac{1}{2}-\frac{1}{2}-\frac{1}{4}+\frac{9}{4}+\left ( 9-\frac{9\pi }{4} \right ) \right ]\)
(b)
\(\int_{3}^{5}2f'(x)+4dx=\int_{3}^{5}2(f'(x)+2)dx\)
\(=2\int_{3}^{5}f'(x)+2dx\)
\(=2\cdot \left [ f(x)+2x \right ]_{3}^{5}\)
\(=2\cdot \left [ \left [ f(5)+2(5) \right ]-\left [ f(3)+2(3) \right ] \right ]\)
(c)
g'(x) = f(x)
g'(x) = f(x) = 0
x = -1, x = 1/2, x = 5
Since f(x) is continuous on -2 ≤ x ≤ 5, then g(x) = \(\int_{-2}^{5}f(t)dt \) is also continuous on -2 ≤ x ≤ 5. Therefore, by the EVT, g(x) has an absolute max. on -2 ≤ x ≤ 5.
Candidates for abs. max : x = -2, -1, 1/2, 5
\(x = -2 : \int_{-2}^{-2}f(t)dt=0\)
\(x = -1 : \int_{-2}^{-1}f(t)dt=\frac{1}{2}\)
\(x = \frac{1}{2} : \int_{-2}^{1/2}f(t)dt=\frac{1}{2}-\frac{1}{2}-\frac{1}{4}=-\frac{1}{4}\)
\(x = 5 : \int_{-2}^{-5}f(t)dt=-\frac{1}{4}+\frac{9}{4}+\left ( 9-\frac{\pi }{4} \right )=2+9-\frac{9\pi }{4}=11-\frac{9\pi }{4}\)
The absolute maximum value of g is \(11-\frac{9\pi }{4}\) and the absolute maximum occurs at x = 5.
(d)
\(\lim_{x\rightarrow 1}10^{x}-3f'(x)=10-3f'(1)=10-3(2)=4\)
\(\lim_{x\rightarrow 1}f(x)-arctan x=1-\frac{\pi }{4}\)
\(arctan(1)=\frac{\pi }{4}\)
\(\lim_{x\rightarrow 1}\frac{10^{x}-3f'(x)}{f(x)-arctan x}=\frac{4}{1-\pi /4}\)
Question
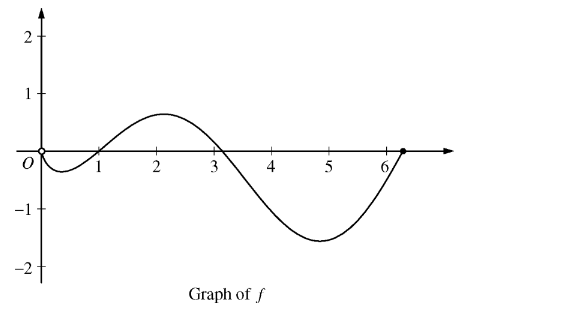
Let f be the function given by f(x)=(Inx)(sinx).The figure above shows the graph of f for \(0<x\leq 2\pi \) The function g is defined by g(x )=\(g(x)=\int_{1}^{x}f(t) dt for 0<x\leq2 \pi \).
(a) Find g(1) and g'(1)
(b) On what intervals, if any, is g increasing? Justify your answer.
(c) For \(0<x\leq 2\pi \), find the value of x at which g has an absolute minimum. Justify your answer.
(d) For \(0<x\leq 2\pi \)is there a value of x at which the graph of g is tangent to the x-axis? Explain why or why not.
▶️Answer/Explanation
(a)\(g(1)=\int_{1}^{1}f(t)dt=0\) and \(g'(1)=f(1)=0 (b) \)Since g'(x) = f(x), g is increasing on the interval 1≤ x ≤ because \(f(x) > 0 for 1 < x < \pi.\) (c) For\( 0 < x < 2\pi, g'(x) = f(x) = 0\) when x = 1, \pi. g’ f changes from negative to positive only at x = 1. The absolute minimum must occur at x = 1 or at the right endpoint. Since g(1) = 0 and \(g(2\pi)=\(\int_{1}^{2\pi}f(t)dt=\int_{1}^{\pi}f(t)dt+\int_{\pi}^{2\pi}f(t)<0\) by comparison of the two areas, the absolute minimum occurs at \(x = 2π.\)
(d) Yes, the graph of g is tangent to the x-axis at x = 1 since g(1) = 0 and g'(1) = 0.
