Question:
At the beginning of 2010, a landfill contained 1400 tons of solid waste. The increasing function W models the total amount of solid waste stored at the landfill. Planners estimate that W will satisfy the differential equation \(\frac{dW}{dt}=\frac{1}{25}(W-300)\) for the next 20 years. W is measured in tons, and t is measured in years from the start of 2010.
(a) Use the line tangent to the graph of W at t = 0 to approximate the amount of solid waste that the landfill contains at the end of the first 3 months of 2010 \(\left ( time t = \frac{1}{4} \right )\).
(b) Find \(\frac{d^{2}W}{dt^{2}}\) in terms of W. Use \(\frac{d^{2}W}{dt^{2}}\) to determine whether your answer in part (a) is an underestimate or an overestimate of the amount of solid waste that the landfill contains at time \(t = \frac{1}{4}\).
(c) Find the particular solution W = W(t) to the differential equation \(\frac{dW}{dt}=\frac{1}{25}(W-300)\) with initial condition W(0) = 1400.
▶️Answer/Explanation
Ans:
(a)
at t = 0, W = 1400
so
\(\frac{dW}{dt}|_{t=0} = \frac{1}{25}(1100)=44 tons/ year = W'(0)\)
W(x + a) ≈ W(λ) + aW'(x)
\(W\left ( 0+\frac{1}{4} \right )\approx W(0)+\frac{1}{4}W'(0)\)
\(W\left ( \frac{1}{4} \right )\approx 1400 + 11\)
\(W\left ( \frac{1}{4} \right )\approx 1411 tons\)
There will be about 1411 tons of landfill after 3 months.
(b)
\(\frac{dW}{dt}=\frac{1}{25}W-12\)
\(\frac{d^{2}W}{dt^{2}}=\frac{1}{25}\frac{dW}{dt}\)
\(\frac{d^{2}W}{dt^{2}}=\frac{1}{625}(W-300)\)
so \(\frac{d^{2}W}{dt^{2}}\) is always positive
b/c W > 300.
The answer in part a is an under estimate because since \(\frac{d^{2}W}{dt^{2}}\) is always positive for t > 0, the graph of W is concave up, so the linearization of W is an underestimate.
(c)
\(\frac{dW}{dt}=\frac{1}{25}(W-300)\)
\(\int \frac{dw}{W-300}=\int \frac{1}{25}dt\)
\(e^{\xi n}\left | W-300 \right |=\frac{1}{25}t+c\)
can remove abs value
b/c W > 300. (iner fn)
[W – 300] = (e 1/25 t
Initial condition w(0) = 1400
1400-300 = C e0
1100 = C
W – 300 = 1100 e 1/25 t
W = W(t) = 1100 e 1/25 t + 300
Question:
Consider the differential equation \(\frac{dy}{dx}=e^{y}(3x^{2}-6x).\) Let y = f (x) be the particular solution to the differential equation that passes through (1 , 0) .
(a) Write an equation for the line tangent to the graph of f at the point (1, 0) . Use the tangent line to approximate f (1, 2).
(b) Find y = f(x), the particular solution to the differential equation that passes through (1, 0).
▶️Answer/Explanation
Ans:
(a)
\(\frac{dy}{dx}= e^{0}(3-6)\)
\(\frac{dy}{dx}= -3\)
y – 0 = -3 (x-1)
y = -3x + 3
y (1.2) = -3(1.2) + 3
y = -.6
(b)
\(\int \frac{1}{e^{y}}dy = \int 3x^{2}-6x dx\)
e-y -e-y = x3 – 3x2 + c
e-y = -x3 – 3x2 + c
-y = -en ( -x3 – 3x2 + c)
0 = – en(-(1)3 + 3 + c)
0 = – en (-1+3+c)
0 = – en (2 + c)
2 + c = 1
c = -1
y = – en ( -x3 + 3x2 + c)
Question:
Consider the differential equation \(\frac{dy}{dx}= (3-y)cos x.\) Let y = f(x) be the particular solution to the differential equation with the initial condition f(0) = 1 . The function f is defined for all real numbers.
(a) A portion of the slope field of the differential equation is given below. Sketch the solution curve through the point (0, 1).
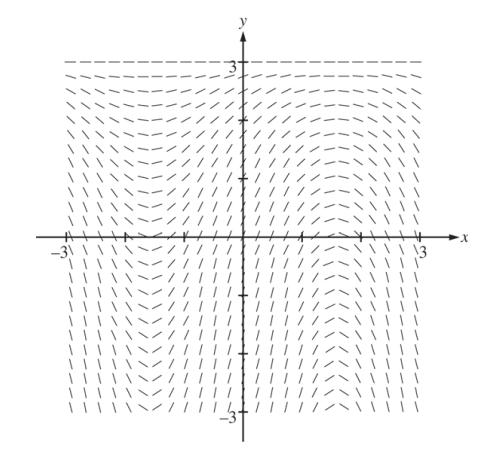
(b) Write an equation for the line tangent to the solution curve in part (a) at the point (0, 1) . Use the equation to approximate f(0.2) .
(c) Find y = f (x), the particular solution to the differential equation with the initial condition f(0) = 1 .
▶️Answer/Explanation
Ans:
(a)
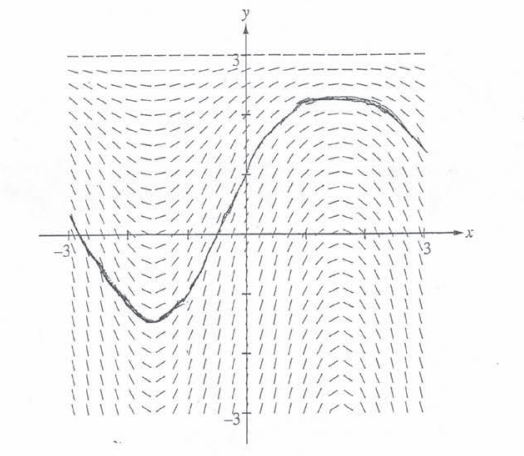
(b)
\(\frac{dy}{dx}= (3-y)cos x = m\)
\(\frac{dy}{dx}= (3-1)cos (0) = m\)
\(m = 2\)
\(y – 1 = 2(x-0)\)
\(y -1 = 2x\)
\(y = 2x + 1\)
\(y – 1 = 2(0.2 – 0)\)
\(y – 1 = 0.4\)
\(y = 1.4\)
\(f(0.2) ≈ 1.4\)
(c)
\(\int \frac{dy}{3-y}=\int cos x dx\) \(3 – y = u\)
\(-\int \frac{du}{u}=sin x + c\) \(du = -dx\)
\(- In |u| = sin x + c\)
\(- In |3-y| = sin x + c\) \(- In |3-y| = sin x – In 2\)
\(- In |3-1| = sin (0) + c \) \(In |3-y| = In 2 – sin x\)
\(- In |2| = 0 + c\) |3 – y| = eIn2 – sin x
\(c = – In 2\) \(\left | 3-y \right |= \frac{e^{In2}}{e^{sinx}}\)
|3-y| = 2e-sinx
3-y = 2e-sinx
-y = 2e-sinx 3
y = -2e-sinx + 3
Question:
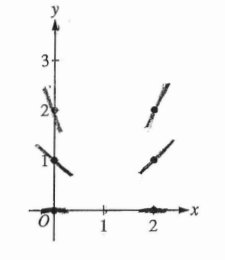
Consider the differential equation \(\frac{dy}{dx}= \frac{y^{2}}{x – 1}.\)
(a) On the axes provided, sketch a slope field for the given differential equation at the six points indicated.
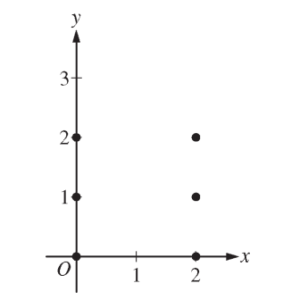
(b) Let y = f(x) be the particular solution to the given differential equation with the initial condition f (2) = 3. Write an equation for the line tangent to the graph of y = f(x) at x = 2.
Use your equation to approximate f(2.1).
(c) Find the particular solution y = f(x) to the given differential equation with the initial condition f (2) = 3.
▶️Answer/Explanation
Ans:
(a)
(b)
\(\frac{dy}{dx}= \frac{y^{2}}{x – 1}|_{(x,y)=(2, 3)}= \frac{9}{2-1}=\frac{9}{1}=9\)
y – 3 = 9 (x-2)
y = 9x – 18 + 3 = 9x – 15
y = 9(2.1) – 15 = 18.9 – 15 = 3.9
(c)
\(\frac{dy}{dx}= \frac{y^{2}}{x – 1}\)
\(\int \frac{dy}{y^{2}}=\int \frac{dx}{x-1}\)
\(\frac{y^{-1}}{-1}=ln|x-1| + c\)
\(\frac{-1}{y}=ln|x-1| + c\)
\(\frac{-1}{3}=ln|2-1| + c\)
\(\frac{-1}{3}=ln1 + c\)
\(c =\frac{-1}{3}\)
\(\frac{-1}{y} =ln(x-1)+\left ( \frac{-1}{3} \right )\)
\(-1 = \left ( ln (x-1)-\frac{1}{3} \right )y\)
\(y = \frac{-1}{ln (x-1)-\frac{-1}{3}}\)
Question:
Consider the differential equation \(\frac{dy}{dx}=\frac{1}{3}x(y-2)^{2}.\)
(a) A slope field for the given differential equation is shown below. Sketch the solution curve that passes through the point (0, 2), and sketch the solution curve that passes through the point (1, 0).
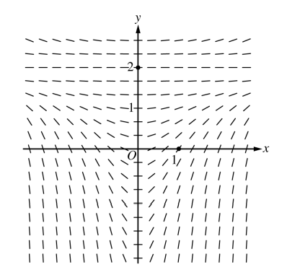
(b) Let y = f (x) be the particular solution to the given differential equation with initial condition f (1) = 0. Write an equation for the line tangent to the graph of y = f (x) at x = 1. Use your equation to approximate f (0.7).
(c) Find the particular solution y = f (x) to the given differential equation with initial condition f (1) = 0.
▶️Answer/Explanation
Ans:
(a)
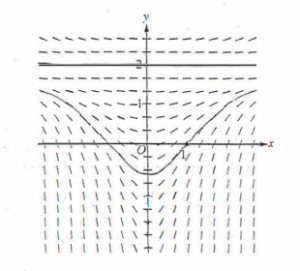
(b)
y = MT (x – 1) + 0 \(M_{T}=\frac{1}{3}\cdot 1(0-2)^{2}\)
y = 4/3 (x – 1) \(=\frac{1}{3}(4)\)
f(0.7) ≈ 4/3 (0.7 – 1) = 4/3
≈ 4/3 (-3/10)
≈ -4/10 = -2/5
(c)
u = y – 2
du = dy
\(\int \frac{dy}{(y-2)^{2}}=\int \frac{1}{3\times dx}\)
\(\int \frac{du}{u^{2}}=\frac{1}{3}\int x dx\)
\(\frac{-1}{4}=\frac{1}{3}\left ( \frac{x^{2}}{2} \right )+c\)
\(\frac{-1}{(y-2)}=\frac{x^{2}}{6}+c\)
point : x = 1
y = 0
\(c = \frac{1}{2}-\frac{1}{6}=\frac{3}{6}-\frac{1}{6}=\frac{2}{6}=\frac{1}{3}\)
\(\therefore \frac{-1}{y-2}=\frac{x^{2}}{6}+\frac{1}{3}\)
\(\frac{1}{y-2}=\frac{-x^{2}}{6}-\frac{1}{3}\)
\(y – 2 = \left ( \frac{1}{\frac{-x^{2}}{6}-\frac{2}{6}} \right )^{6/6}\)
\(y – 2 = \frac{b}{-(x^{2}+2)}\)
\(y = \frac{6}{-(x^{2}+2)}+2\)
Question:
A medication is administered to a patient. The amount, in milligrams, of the medication in the patient at time t hours is modeled by a function y = A(t ) that satisfies the differential equation \(\frac{dy}{dt}=\frac{12-y}{3}.\) At time t = 0 hours, there are 0 milligrams of the medication in the patient.
(a) A portion of the slope field for the differential equation \(\frac{dy}{dt}=\frac{12-y}{3}\) is given below. Sketch the solution curve through the point (0, 0).
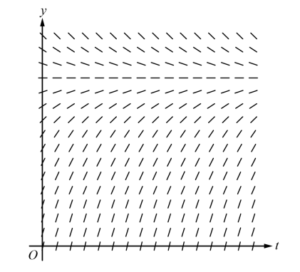
(b) Using correct units, interpret the statement \(\lim_{t\rightarrow \infty }A(t)=12\) in the context of this problem.
(c) Use separation of variables to find y = A(t), the particular solution to the differential equation \(\frac{dy}{dt}=\frac{12-y}{3}\) with initial condition A(0) = 0.
(d) A different procedure is used to administer the medication to a second patient. The amount, in milligrams, of the medication in the second patient at time t hours is modeled by a function y = B(t) that satisfies the differential equation \(\frac{dy}{dt}=3 – \frac{y}{t+2}.\) At time t = 1 hour, there are 2.5 milligrams of the medication in the second patient. Is the rate of change of the amount of medication in the second patient increasing or decreasing at time t = 1 ? Give a reason for your answer.
▶️Answer/Explanation
Ans:
(a)
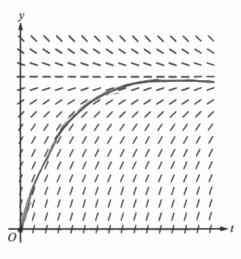
(b)
As time goes to infinity, the amount of medication in the patient, in milligrams, is approaching 12.
(c)
\(\frac{dy}{dt}=\frac{12-y}{3}\)
\(\int \frac{dy}{12-y}=\int \frac{dt}{3}\)
\(-en|12-y| = \frac{1}{3}t+c\) \(-en|12-y| = \frac{1}{3}t-en 12\)
\(-en|12-0| = \frac{1}{3}(0)+c\) \(en|12-y| = \frac{1}{3}t+en 12\)
c = -en 12 \(e^{en|12-y|} = e^{-\frac{1}{3}t+en 12}\)
\(12-y = e^{-\frac{1}{3}t}.e^{en 12}\)
\(12-y = 12e^{-\frac{1}{3}t}\)
\(-y = 12e^{-\frac{1}{3}t}-12\)
\(y = -12e^{-\frac{1}{3}t}+12\)
(d)
\(\frac{dy}{dt}=3 – \frac{y}{t+2}\)
\(\frac{d^{2}y}{dt^{2}}=-\frac{dy/dx(t+2)-1(y)}{(t+2)^{2}}\)
\(\frac{d^{2}y}{dt^{2}}=-\frac{\left ( 3-\frac{y}{t+2} \right )(t+2)-y}{(t+2)^{2}}\)
\(\frac{d^{2}y}{dt^{2}}|_{(1, 2.5)}=-\frac{\left ( 3-\frac{2.5}{1+2} \right )(1+2)-2.5}{(1+2)^{2}}=\frac{\left ( 3-\frac{5}{3} \right )(3)-2.5}{3^{2}}=\sim \) #
Question50
Consider the differential equation \(\frac{dy}{dx}=\frac{x}{y} where y\neq 0\)
(a) The slope field for the given differential equation is shown below. Sketch the solution curve that passes through the point ( 3,- 1 ), and sketch the solution curve that passes through the point ( 1, 2) .(Note: The points ( 3, -1) and ( 1, 2) are indicated in the figure.)
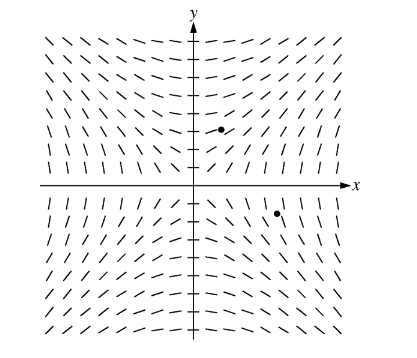
(b) Write an equation for the line tangent to the solution curve that passes through the point ( 1, 2) .
(c) Find the particular solution y = f ( x) to the differential equation with the initial condition f ( 3 ), = -1 and state its domain
▶️Answer/Explanation
.
(a)\(g(1)=\int_{1}^{1}f(t)dt=0 \)and \(g'(1)=f(1)=0 \)(b) Since g'(x) = f(x), g is increasing on the interval 1≤ x ≤ because \(f(x) > 0 for 1 < x < \pi.\) (c) For \(0 < x < 2\pi, g'(x) = f(x) = 0 \)when x = 1, \pi. g’ f changes from negative to positive only at x = 1. The absolute minimum must occur at x = 1 or at the right endpoint. Since g(1) = 0 and \(g(2\pi)=\int_{1}^{2\pi}f(t)dt=\int_{1}^{\pi}f(t)dt+\int_{\pi}^{2\pi}f(t)<0\) by comparison of the two areas, the absolute minimum occurs at \(x = 2π. \)(d) Yes, the graph of g is tangent to the x-axis at x = 1 since g(1) = 0 and g'(1) = 0.
