Question:
For 0 ≤ t ≤ 6, a particle is moving along the x-axis. The particle’s position, x (t), is not explicitly given.
The velocity of the particle is given by \(v(t)=2sin\left ( e^{t/4} \right )+1.\) The acceleration of the particle is given by \(a(t)=\frac{1}{2}e^{t/4}cos\left ( e^{t/4} \right )\) and x(0) = 2.
(a) Is the speed of the particle increasing or decreasing at time t = 5.5 ? Give a reason for your answer.
(b) Find the average velocity of the particle for the time period 0 ≤ t ≤ 6.
(c) Find the total distance traveled by the particle from time t = 0 to t = 6.
(d) For 0 ≤ t ≤ 6,the particle changes direction exactly once. Find the position of the particle at that time.
▶️Answer/Explanation
Ans:
(a) The speed is increasing at t = 5.5 because v(5.5) < 0 and a(5.5) < 0
v (5.5) = -0.453
a (5.5) = -1.358
(b)
\(\frac{1}{6-0}\int_{0}^{6}v(t)dt = 1.949\)
(c)
\(\int_{0}^{6}\left | v(t) \right |dt = 12.573\)
(d)
v(t) = 0 at t=5.1955223 and v(t) changes sign at t = 5.1955223
\(X(5.195223)= 2+\int_{0}^{5.195523}v(t)dt\)
Position at t = 5.195523 is 14.134
Question:
| t (minutes) | 0 | 2 | 5 | 9 | 10 |
H(t) | 66 | 60 | 52 | 44 | 43 |
As a pot of tea cools, the temperature of the tea is modeled by a differentiable function H for 0 ≤ t ≤ 10, where time t is measured in minutes and temperature H(t) is measured in degrees Celsius. Values of H(t) at selected values of time t are shown in the table above.
(a) Use the data in the table to approximate the rate at which the temperature of the tea is changing at time t = 3.5. Show the computations that lead to your answer.
(b) Using correct units, explain the meaning of \(\frac{1}{10}\int_{0}^{10}H(t)dt\) in the context of this problem. Use a trapezoidal sum with the four subintervals indicated by the table to estimate \(\frac{1}{10}\int_{0}^{10}H(t)dt\).
(c) Evaluate \(\frac{1}{10}\int_{0}^{10}H'(t)dt\). Using correct units, explain the meaning of the expression in the context of this problem.
(d) At time t = 0, biscuits with temperature 100 C∞ were removed from an oven. The temperature of the biscuits at time t is modeled by a differentiable function B for which it is known that \(B'(t)=-13.84e^{-0.173t}.\) Using the given models, at time t = 10, how much cooler are the biscuits than the tea?
▶️Answer/Explanation
Ans:
(a) \(\frac{H(5)-H(2)}{5-2}=\frac{-8}{3}\frac{0_{C}}{min}\)
(b) \(\frac{1}{10}\int_{0}^{10}H(t)dt \approx \frac{\left [ 2\left ( \frac{66+60}{2} \right )+3\left ( \frac{52+60}{2} \right ) +4\left ( \frac{44+52}{2} \right )+1\left ( \frac{43+44}{2} \right )\right ]}{10}=52.95\)
This represents the average temperature in degrees celsius of the Tea over the interval 0 ≤ t ≤ 10
(c)
\(\int_{0}^{10}H'(t)dt = H(10)-H(0)=43-66 = -23^{0}C\)
This expression shows the total change in temperature in degree Celsius from t = 0 to t = 10.
(d)
\( B'(t)= -13.84e^{-1.73t}\)
\(B(10)= \int_{0}^{10}-13.84e^{-1.73t}+100 = 100-65.817 = 34.1827\)
43 – 34.1827 = 8.817
= 8.817 0C
Question:
| t (minutes) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| C (t) (ounces) | 0 | 5.3 | 8.8 | 11.2 | 12.8 | 13.8 | 14.5 |
Hot water is dripping through a coffeemaker, filling a large cup with coffee. The amount of coffee in the cup at time t, 0 ≤ t ≤ 6, is given by a differentiable function C, where t is measured in minutes. Selected values of C (t), measured in ounces, are given in the table above.
(a) Use the data in the table to approximate C'(3.5) . Show the computations that lead to your answer, and indicate units of measure.
(b) Is there a time t, 2 ≤ t ≤ 4 at which C’ (t)= 2 ? Justify your answer.
(c) Use a midpoint sum with three subintervals of equal length indicated by the data in the table to approximate the value of \(\frac{1}{6}\int_{0}^{6}C(t)dt.\) Using correct units, explain the meaning of \(\frac{1}{6}\int_{0}^{6}C(t)dt\) in the context of the problem.
(d) The amount of coffee in the cup, in ounces, is modeled by \(B(t)= 16-16e^{-0.4t}\). Using this model, find the rate at which the amount of coffee in the cup is changing when t = 5.
▶️Answer/Explanation
Ans:
(a)
\(C'(3.5)\approx \frac{\left ( (4)-(3) \right )}{4-3}=\frac{12.8-11.2}{1}=1.6\frac{08}{min}\)
(b)
Since C(t) is differentiable for all values is [2, 4], we can say that there must be some value of t in (2, 4), such as t = a, such that \(C'(a)=\frac{\left ( (4)-(2) \right )}{4-2}=\frac{12.8-8.8}{2}=2\) by the mean value theorem
so, yes’.
(c)
\(\frac{1}{6}\int_{0}^{6}C(t)dt \approx \frac{1}{6}-2.(5.3+11.2+13.8)\)
≈ 10.1 0t
This is the average value, in oz, of the amount of coffee in the cup over the interval 0 ≤ t ≤ 6.
(d)
\(B'(t)= \frac{32}{5}e^{-0.4t}\)
\(B'(5)= \frac{32}{5}e^{-2}\)
Question:
Grass clippings are placed in a bin, where they decompose. For 0 ≤ t ≤ 30 , the amount of grass clippings remaining in the bin is modeled by A(t) = 6.687 (0.931)t , where A (t) is measured in pounds and t is measured in days.
(a) Find the average rate of change of A (t) over the interval 0 ≤ t ≤ 30 . Indicate units of measure.
(b) Find the value of A'(15) . Using correct units, interpret the meaning of the value in the context of the problem.
(c) Find the time t for which the amount of grass clippings in the bin is equal to the average amount of grass clippings in the bin over the interval 0 ≤ t ≤ 30.
(d) For t > 30, L(t), the linear approximation to A at t = 30, is a better model for the amount of grass clippings remaining in the bin. Use L (t) to predict the time at which there will be 0.5 pound of grass clippings remaining in the bin. Show the work that leads to your answer.
▶️Answer/Explanation
Ans:
(a)
\(\frac{A(30)-A(0)}{30-0}=\frac{-5.904}{30}\approx -.197\frac{pounds}{day}\)
(b)
A'(t) = – .478(.931)t
A'(15) = -.164 \(\frac{pounds}{day}\)
The amount of grass clippings in the bin is decreasing (decomposing) at a rate of .164 pounds per day at time = 15 days
(c)
Average amount \(=\frac{1}{30}\int_{0}^{30}A(t)dt = 2.75263511\)
A(t) = 2.75263511 = 6.687 (.931)t
this occurs at t = 12.414 days
(d)
L(t) is the tangent line to A(t) at t = 30
A(30) = .783 ⇒ (30, .783) = (t, A(t))
A'(30) = -.056 let -.056 = M
(y-y1) = m (x, x1) so for this problem,
(A(t) – .783) = -.056(t-30)
When there are .5 pounds of grass, A(t) = .5,
(.5-.783) = -.056(t-30)
t = 35.054 days
Question:
| t (minutes) | 0 | 12 | 20 | 24 | 40 |
| v (t) (meters per minute) | 0 | 200 | 240 | -220 | 150 |
Johanna jogs along a straight path. For 0 ≤ t ≤ 40, Johanna’s velocity is given by a differentiable function v.
Selected values of v (t), where t is measured in minutes and v (t) is measured in meters per minute, are given in the table above.
(a) Use the data in the table to estimate the value of v'(16).
(b) Using correct units, explain the meaning of the definite integral \(\int_{0}^{40}|v(t)|dt\) in the context of the problem.
Approximate the value of \(\int_{0}^{40}|v(t)|dt\) using a right Riemann sum with the four subintervals indicated in the table.
(c) Bob is riding his bicycle along the same path. For 0 ≤ t ≤ 10, Bob’s velocity is modeled by B(t) = t3 – 6t + 300, where t is measured in minutes and B (t) is measured in meters per minute.
Find Bob’s acceleration at time t = 5.
(d) Based on the model B from part (c), find Bob’s average velocity during the interval0 ≤ t ≤ 10.
▶️Answer/Explanation
Ans:
(a)
\(V'(14)\approx \frac{v(20)-v(12)}{20-12}=\frac{240-200}{8}=\frac{40}{8}=\frac{20}{4}=5\frac{m}{min^{2}}\)
(b)
\(\int_{0}^{40}|v(t)|dt\) represents the total distance in meters Johanna traveled between times. t = 0 and t = 40 minutes.
\(\int_{0}^{40}|v(t)|dt\approx \left [ 12(200)+8(240)+4(220)+16(150) \right ]\)
= 2400 + 1920 + 880 + 2400
= 7600 meters
(c)
acceleration = B'(t) = 3t2 – 12t
B'(5) = 3(5)2 – 12(5)
= 75-60 = 15 \(\frac{m}{min^{2}}\)
(d)
Avg. Velocity = \(\frac{1}{10}\int_{0}^{10}(t^{3}-6t^{2}+300)dt\)
\(=\frac{1}{10}\cdot \left [ \frac{t^{4}}{4} -2t^{3}+300t\right ]_{0}^{10}\)
\(=\frac{1}{10}\cdot \left [ \frac{10000}{4} -2000+300t\right ]\)
\(=\frac{1}{10}\left [ 3500\right ]=350\frac{m}{min}\)
Question:
| t (minutes) | 0 | 12 | 20 | 24 | 40 |
| v (t) (meters per minute) | 0 | 200 | 240 | -220 | 150 |
Johanna jogs along a straight path. For 0 ≤ t ≤ 40, Johanna’s velocity is given by a differentiable function v.
Selected values of v (t), where t is measured in minutes and v (t) is measured in meters per minute, are given in the table above.
(a) Use the data in the table to estimate the value of v'(16).
(b) Using correct units, explain the meaning of the definite integral \(\int_{0}^{40}|v(t)|dt\) in the context of the problem.
Approximate the value of \(\int_{0}^{40}|v(t)|dt\) using a right Riemann sum with the four subintervals indicated in the table.
(c) Bob is riding his bicycle along the same path. For 0 ≤ t ≤ 10, Bob’s velocity is modeled by B(t) = t3 – 6t + 300, where t is measured in minutes and B (t) is measured in meters per minute.
Find Bob’s acceleration at time t = 5.
(d) Based on the model B from part (c), find Bob’s average velocity during the interval0 ≤ t ≤ 10.
▶️Answer/Explanation
Ans:
(a)
\(V'(14)\approx \frac{v(20)-v(12)}{20-12}=\frac{240-200}{8}=\frac{40}{8}=\frac{20}{4}=5\frac{m}{min^{2}}\)
(b)
\(\int_{0}^{40}|v(t)|dt\) represents the total distance in meters Johanna traveled between times. t = 0 and t = 40 minutes.
\(\int_{0}^{40}|v(t)|dt\approx \left [ 12(200)+8(240)+4(220)+16(150) \right ]\)
= 2400 + 1920 + 880 + 2400
= 7600 meters
(c)
acceleration = B'(t) = 3t2 – 12t
B'(5) = 3(5)2 – 12(5)
= 75-60 = 15 \(\frac{m}{min^{2}}\)
(d)
Avg. Velocity = \(\frac{1}{10}\int_{0}^{10}(t^{3}-6t^{2}+300)dt\)
\(=\frac{1}{10}\cdot \left [ \frac{t^{4}}{4} -2t^{3}+300t\right ]_{0}^{10}\)
\(=\frac{1}{10}\cdot \left [ \frac{10000}{4} -2000+300t\right ]\)
\(=\frac{1}{10}\left [ 3500\right ]=350\frac{m}{min}\)
Question:
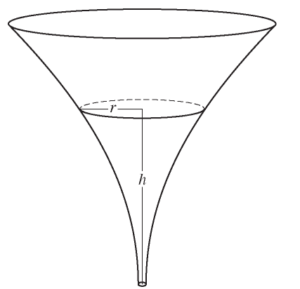
The inside of a funnel of height 10 inches has circular cross sections, as shown in the figure above. At height h, the radius of the funnel is given by \(r = \frac{1}{20}\left ( 3+h^{2} \right ),\) where 0 ≤ h ≤ 10. The units of r and h are inches.
(a) Find the average value of the radius of the funnel.
(b) Find the volume of the funnel.
(c) The funnel contains liquid that is draining from the bottom. At the instant when the height of the liquid is h = 3 inches, the radius of the surface of the liquid is decreasing at a rate of \(\frac{1}{5}\) inch per second. At this instant, what is the rate of change of the height of the liquid with respect to time?
▶️Answer/Explanation
Ans:
(a)
\(r_{avg}= \frac{1}{200}\int_{0}^{10}\left ( 3+h^{2} \right )dh\)
\(= \frac{1}{200}\left ( 3h+\frac{h^{3}}{3} \right )_{0}^{10}\textrm{]}\)
\(= \frac{1}{200}\left ( 30+\frac{1000}{3} \right )\)
\(= \frac{109}{60} inches.\)
(b)
\(v = \frac{\pi }{400}\int_{0}^{10}(3+h)^{2}dh\)
\(= \frac{\pi }{400}\int_{0}^{10}(9+6h^{2}+h^{4})dh\)
\(= \frac{\pi }{400}(9h+2h^{3}+\frac{h^{5}}{5})_{0}^{10}\textrm{]}\)
\(= \frac{\pi }{400}(90+2000+20000)\)
\(= \frac{2209\pi }{40}in^{3}\)
(c)
\(r = \frac{1}{20}(3+h^{2})\)
\(\frac{dr}{dt}= \left ( \frac{h}{10} \right )\frac{dh}{dt}\)
\(-\frac{1}{5}= \frac{3}{10}\frac{dh}{dt}\)
\(\frac{dh}{dt}= -\frac{2}{3}\) inch per second
Question:
The density of a bacteria population in a circular petri dish at a distance r centimeters from the center of the dish is given by an increasing, differentiable function f , where f (r) is measured in milligrams per square centimeter. Values of f (r) for selected values of r are given in the table above.
(a) Use the data in the table to estimate f'(2.25). Using correct units, interpret the meaning of your answer in the context of this problem.
(b) The total mass, in milligrams, of bacteria in the petri dish is given by the integral expression \(2\pi \int_{0}^{4}r f(r)dr.\) Approximate the value of \(2\pi \int_{0}^{4}r f(r)dr\) using a right Riemann sum with the four subintervals indicated by the data in the table.
(c) Is the approximation found in part (b) an overestimate or underestimate of the total mass of bacteria in the petri dish? Explain your reasoning.
(d) The density of bacteria in the petri dish, for 1 ≤ r ≤ 4, is modeled by the function g defined by \(g(r)=2-16(cos (1.57\sqrt{r}))^{3}.\) For what value of k , 1 < k < 4, is g (k) equal to the average value of g (r) on the interval 1 ≤ r ≤ 4 ?
▶️Answer/Explanation
Ans:
(a)
\(f'(2.25)\approx \frac{f(2.5)-f(2)}{2.5-2}=\frac{10-6}{0.5}=\frac{4}{0.5}=8\) milligrams per square centimeter per centimeters.
The density of bacteria changes at a rate of approximately 8 milligrams per square centimeter per centimeter at distance r = 2.25 centimeters. From the center of the dish
(b)
\(2\pi \int_{0}^{9}r\cdot f(r)dr\approx 2\pi \cdot (2.1-1+6.1.2+10.0.5.2.5+18.1.5.4)\)
\(2\pi (2+12+12.5+108)=2\pi (13+.5)=269\pi milligrams\)
(c)
As a rule, Right Riemann sums are always an over estimate for functions with positive slove, and underestimates for functions with negative slope. The slope of r.f(r) is equal to r’.f(r) +r.f'(r). Since r, r’, f(r), and f'(r) are always positive on the internal [0, 4], r.f(r) always has a positive slope on that internal. Since it’s a positive sloped functions, the right Riemann sum for r.f(r) from 0 to 9 is an over estimate.
(d)
Avg of g(r) \(=\frac{1}{4-1}\int_{1}^{4}(2-16(cos(1.57\sqrt{r}))^{3})dr=\frac{29.627}{3}=9.876\)
\(g(k)= 2 – 16 (cos(1.57\sqrt{k}))^{3}=9.876\)
k = 2.497
Question
The temperature, in degrees Celsius \((^{\circ}C) \), of an oven being heated is modeled by an increasing differentiable function H of time t, where t is measured in minutes. The table above gives the temperature as recorded every 4 minutes over a 16-minute period.
(a) Use the data in the table to estimate the instantaneous rate at which the temperature of the oven is changing at time t = 10. Show the computations that lead to your answer. Indicate units of measure.
(b) Write an integral expression in terms of H for the average temperature of the oven between time t =0 and time t = 16. Estimate the average temperature of the oven using a left Riemann sum with four subintervals of equal length. Show the computations that lead to your answer.
(c) Is your approximation in part (b) an underestimate or an overestimate of the average temperature? Give a reason for your answer.
▶️Answer/Explanation
(d) Are the data in the table consistent with or do they contradict the claim that the temperature of the oven is increasing at an increasing rate? Give a reason for your answer.
(a)\(H’=\frac{H(12)-H(8)}{12-8}\)=\(\frac{80-73}{4}\)=\(\frac{7}{4}^{\circ}C/min\)
(b)Average temperature is \(\frac{1}{16}H(t)dt\)
\(\int_{0}^{16}H(t)dt\simeq 4.(65+68+73+80)\)
Average temperature\( \simeq \frac{4.286}{16}=71.5^{\circ}C\)
(c) The left Riemann sum approximation is an underestimate of the integral because the graph of H is increasing. Dividing by 16 will not change the inequality, so 71.5°C is an underestimate of the average temperature.
(d) If a continuous function is increasing at an increasing rate, then the slopes of the secant lines of the graph of the function are increasing. The slopes of the secant lines for the four intervals in the table are \(\frac{3}{4}\), \(\frac{5}{4}\),\(\frac{7}{4}\)and\( \frac{10}{4}\), respectively. Since the slopes are increasing, the data are consistent with the claim. OR By the Mean Value Theorem, the slopes are also the values of \(H'(c_{k})\) for some times \(c_1 < C_2 < C_3 < C_4\), respectively. Since these derivative values are positive and increasing, the data are consistent with the claim.
