Question:
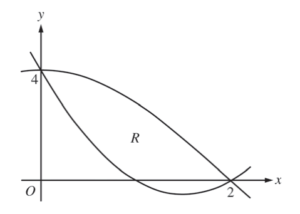
Let R be the region enclosed by the graph of f(x) = x4 – 2.3x3 + 4 and the horizontal line y = 4, as shown in the figure above.
(a) Find the volume of the solid generated when R is rotated about the horizontal line y = -2.
(b) Region R is the base of a solid. For this solid, each cross section perpendicular to the x-axis is an isosceles right triangle with a leg in R. Find the volume of the solid.
(c) The vertical line x = k divides R into two regions with equal areas. Write, but do not solve, an equation involving integral expressions whose solution gives the value k.
▶️Answer/Explanation
Ans:
(a)
\(f(x)= 4| _{x = 0 or 2.3} \) \(\pi \int_{0}^{2.3}\left ( (2+4)^{2}-(2+f(x))^{2} \right )dx = 98.868 units^{3}\)
\(V = \pi \left ( R^{2}-r^{2} \right )\)
(b)
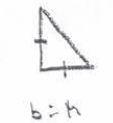
\(A = \frac{1}{2}bh\)
\(A = \frac{1}{2}b^{2}\)
b = 4 – f(x)
\(\frac{1}{2}\int_{0}^{2.3}(4-p(x))^{2}dx= 3.574 units^{3}\)
(c)
\(\int_{0}^{k}(4-f(x))dx= \frac{1}{2}\int_{0}^{2.3}\left ( 4-f(x) \right )dx\)
Question:
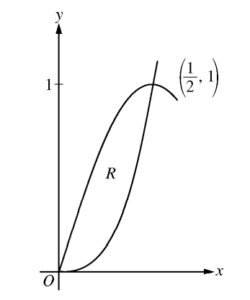
Let R be the region in the first quadrant enclosed by the graphs of f(x) = 8x3 and g(x) = sin(πx) , p as shown in the figure above.
(a) Write an equation for the line tangent to the graph of f at \(x = \frac{1}{2}.\)
(b) Find the area of R.
(c) Write, but do not evaluate, an integral expression for the volume of the solid generated when R is rotated about the horizontal line y = 1.
▶️Answer/Explanation
Ans:
(a)
f(x) = 8x3 \(f\left ( \frac{1}{2} \right ) = 8\left ( \frac{1}{8} \right )=1\) point of tangency : \(\left ( \frac{1}{2}, 1 \right )\)
f'(x) = 24x2 \(f’\left ( \frac{1}{2} \right )= 24 . \frac{1}{4}=6\)
y = 6x + b The tangent line to the graph of f
\(1 = 6\left ( \frac{1}{2} \right )+b\) at \(x = \frac{1}{2}\) is y = 6x-2.
1 = 3 + b
b = -2
y = 6x -2
(b)
f(x) = g(x)
8×3 = sin(πx)
x = 0 , \(\frac{1}{2}\)
\(R = \int_{0}^{\frac{1}{2}}\left [ 9(x)-f(x) \right ]dx = \int_{0}^{\frac{1}{2}}\left [ sin(\pi x)-8x^{3} \right ]dx=\frac{1}{\pi }\int_{0}^{\frac{1}{2}}sinu du – \int_{0}^{\frac{1}{2}}8x^{3}dx\)
\(= \frac{1}{\pi }(-cos(\pi x))_{0}^{\frac{1}{2}}-2x^{4}\) \(_{0}^{\frac{1}{2}}\)
\(= \frac{1}{\pi }(-cos(\frac{\pi }{2})+cos(01))-2\left ( \frac{1}{2} \right )^{4}+0\)
\(= \frac{1}{\pi }(1)-\frac{2}{16}\)
\(= \frac{1}{\pi }-\frac{1}{8}=\frac{8-\pi }{8\pi }\)
(c)
\(\pi \int_{0}^{\frac{1}{2}}\left [ \left ( 1-f(x) \right )^{2}-\left ( 1-9(x) \right )^{2} \right ]dx\)
Question:
Let \(f(x)= 2x^{2}-6x+4\) and \(g(x)= 4 cos \left ( \frac{1}{4}\pi x \right ).\) Let R be the region bounded by the graphs of f and g, as shown in the figure above.
(a) Find the area of R.
(b) Write, but do not evaluate, an integral expression that gives the volume of the solid generated when R is rotated about the horizontal line y = 4.
(c) The region R is the base of a solid. For this solid, each cross section perpendicular to the x-axis is a square.
Write, but do not evaluate, an integral expression that gives the volume of the solid.
▶️Answer/Explanation
Ans:
(a)
\(R = \int_{0}^{2}\left ( 4 cos (\frac{1}{4}\pi x) -(2x^{2}-6x-4)\right )dx\)
\(R = \left ( \frac{16}{\pi } sin(\frac{1}{4}\pi x)-\frac{2}{3x^{3}}+3x^{2}-4x\right )_{0}^{2}\)
\(R = \left ( \frac{16}{\pi } sin(\frac{1}{2}\pi)-\frac{16}{3}+13-8\right )-\left ( \frac{16}{\pi } sin(0)-0+0-0\right )\)
\(R = \frac{16}{\pi }(1)-\frac{16}{3}+4\)
\(R = \frac{16}{\pi }-\frac{4}{3}\)
(b)
\(v = \pi \int_{0}^{2}\left ( 4-(2x^{2}-6x)+4 \right )^{2}-\left ( 4-4cos(\frac{1}{4}\pi x)\right )^{2}dx\)
\(v = \pi \int_{0}^{20}\left ( 2x^{2}+6x \right )^{2}-\left ( 4-4cos(\frac{1}{7}\pi x)\right )^{2}dx\)
(c)
\(v = \int_{0}^{2}\left ( 4cos(\frac{1}{4}\pi x)-( 2x^{2}-6x+4)\right )^{2}dx\)
\(v = \int_{0}^{2}\left ( 4cos(\frac{1}{4}\pi x)-( 2x^{2}+6x-4)\right )^{2}dx\)
Question:
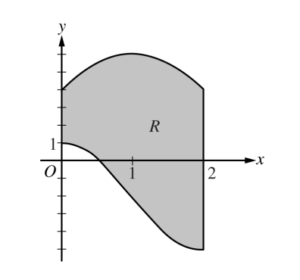
Let R be the region enclosed by the graphs of \(g(x)= -2 + 3 cos \left ( \frac{\pi }{2}x \right )\) and h(x) = 6 – 2(x-1)2, the y-axis, and the vertical line x = 2, as shown in the figure above.
(a) Find the area of R.
(b) Region R is the base of a solid. For the solid, at each x the cross section perpendicular to the x-axis has area \(A(x)=\frac{1}{x+3}.\) Find the volume of the solid.
(c) Write, but do not evaluate, an integral expression that gives the volume of the solid generated when R is rotated about the horizontal line y = 6.
▶️Answer/Explanation
Ans:
(a)
\(Area = \int_{0}^{2}h(x)-g(x)dx\)
\( = \int_{0}^{2}6-2(x-1)^{2}dx – \int_{0}^{2}-2+3 cos (\frac{\pi }{2}x)dx\)
\(=6x – \frac{2}{3}(x-1)^{3}|_{0}^{2}-\left ( -2x+\frac{6}{\pi }sin(\frac{\pi }{2}x) \right )|_{0}^{2}\)
\(=\left ( \left [ 12-\frac{2}{3}(1) \right ]-\left [ 0+\frac{2}{3} \right ] \right )-\left ( \left [ -4+\frac{6}{\pi }(0) \right ]-\left [ 0+0 \right ] \right )\)
\(=12-\frac{4}{3}+4=16-\frac{4}{3}\)
(b)
\(v = \int_{0}^{2}A(x)2x=\int_{0}^{2}\frac{1}{x+3}dx=ln|x+3||_{0}^{2}=ln |5| – ln |3|\)
= ln 5- ln 3
(c)
\(v = \int_{0}^{2}\pi \left [ (4-g(x))^{2}-(6-h(x))^{2} \right ]dx\)