Question:
| t (minutes) | 0 | 4 | 9 | 15 | 20 |
| W (t) (degrees Fahrenheit) | 55.0 | 57.1 | 61.8 | 67.9 | 71.0 |
The temperature of water in a tub at time t is modeled by a strictly increasing, twice-differentiable function W, where W (t) is measured in degrees Fahrenheit and t is measured in minutes. At time t = 0, the temperature of the water is 550 F. The water is heated for 30 minutes, beginning at time t = 0. Values of W (t) at selected times t for the first 20 minutes are given in the table above.
(a) Use the data in the table to estimate W'(12) . Show the computations that lead to your answer. Using correct units, interpret the meaning of your answer in the context of this problem.
(b) Use the data in the table to evaluate \(\int_{0}^{20}W'(t)dt.\) Using correct units, interpret the meaning of \(\int_{0}^{20}W'(t)dt\) in the context of this problem.
(c) For 0 ≤ t ≤ 20, the average temperature of the water in the tub is \(\frac{1}{20}\int_{0}^{20}W(t)dt.\) Use a left Riemann sum with the four subintervals indicated by the data in the table to approximate \(\frac{1}{20}\int_{0}^{20}W(t)dt.\) Does this approximation overestimate or underestimate the average temperature of the water over these 20 minutes?
Explain your reasoning.
(d) For 20 ≤ t ≤ 25, the function W that models the water temperature has first derivative given by W'(t) \(= 0.4\sqrt{t }cos (0.06t).\) Based on the model, what is the temperature of the water at time t =25 ?
▶️Answer/Explanation
Ans:
(a)
\(W'(12)\approx \frac{67.9-61.8}{15-9}=1.0167 F/min\)
At t = 12, the temperature of the water in the tub is increasing at the rate of 1.0167 . F/min.
(b)
\(\int_{0}^{20}W'(t)dt = W(20)-W(0)=7.10-55.0 = 16^{0}F\)
\(\int_{0}^{20}W'(t)dt \) is the difference in temperature in 0F of the water in the tub at t = 20 and t = 0.
(c)
\(\int_{0}^{20}W(t)dt \approx 4(55.0)+5(57.1)+6(61.8)+5(67.9)\)
= 1215.8
\(\frac{1}{20}\int_{0}^{20}W(t)dt =60.79^{0}F\)
As the function W(t) is strictly increasing, the approximation rectangles of the left Riemann sum fall. below the curve. Thus the approximation is an under estimate.
(d)
\(\int_{20}^{25}W'(t)= W(25)-W(20)=2.043\)
W(25) – 71.0 = 2.043
W(25) = 73.0432 0F
Question:
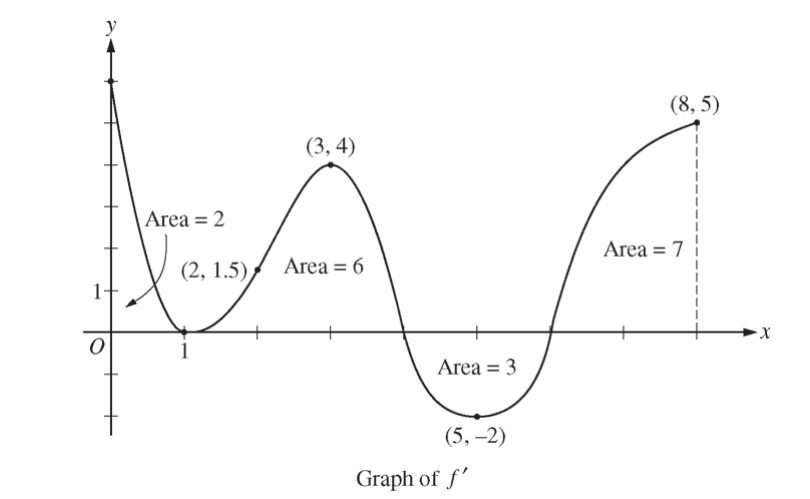
The figure above shows the graph of f’, the derivative of a twice-differentiable function f, on the closed interval 0 ≤ x ≤ 8. The graph of f’ has horizontal tangent lines at x = 1, x = 3, and x = 5. The areas of the regions between the graph of f’ and the x-axis are labeled in the figure. The function f is defined for all real numbers and satisfies f (8) = 4.
(a) Find all values of x on the open interval 0 < x < 8 for which the function f has a local minimum. Justify your answer.
(b) Determine the absolute minimum value of f on the closed interval 0 ≤ x ≤ 8. Justify your answer.
(c) On what open intervals contained in 0 < x < 8 is the graph of f both concave down and increasing? Explain your reasoning.
(d) The function g is defined by \(g(x)=(f(x))^{3}\), if \(f(3)= -\frac{5}{2},\) find the slope of the line tangent to the graph of g at x = 3.
▶️Answer/Explanation
Ans:
(a)
X = 6
f has a local minmum at x = 6, because the graph of f’ changes from negative to positive at x = 6, so using the first derivative test and f has a critical number at x = 6, f has a local minimum
(b)
local minimum = x = 6 f(8) = 4
\(f(6)\rightarrow \int_{6}^{8}f'(x)dx = 7 = f(8)-f(6)=4-f(6)\) f(6) = -3
\(f(0)\rightarrow \int_{0}^{8}f'(x) = 12 = f(8)-f(0)=4-f(0)\) f(0) = -8
The absolute minimum value of f on the interval 0 ≤ x ≤ 8 is -8 because it is the lowest value for the among the endpoints and critical numbers.
(c) \({f}” < 0\)
The open intervals where the graph of f is both concave down and increasing is (0, 1) u (3, 4), or 0 < x < 1 and 3 < x 4, because using the graph of f’, when the graph of f’ is positive and the slope of f’ is negative that means that f is increasing and f” is negative so f is both concave down and increasing.
(d)
g'(x) = 3 (f(x))2. f'(x)
g'(3) = 3 (f(3))2 . f'(3) = 3 (-5/2)2 . (4)
= 3 (25/4)4 = 75
g'(3) = 75
Question:
The rate at which rainwater flows into a drainpipe is modeled by the function R, where \(R(t)=20sin\left ( \frac{t^{2}}{35} \right )\) cubic feet per hour, t is measured in hours, and 0 ≤ t ≤ 8. The pipe is partially blocked, allowing water to drain out the other end of the pipe at a rate modeled by D(t) = -0.04t3 + 0.4t2 + 0.96t cubic feet per hour, for 0 ≤ t ≤ 8. There are 30 cubic feet of water in the pipe at time t = 0.
(a) How many cubic feet of rainwater flow into the pipe during the 8-hour time interval 0 ≤ t ≤ 8?
(b) Is the amount of water in the pipe increasing or decreasing at time t = 3 hours? Give a reason for your answer.
(c) At what time t, 0 ≤ t ≤ 8, is the amount of water in the pipe at a minimum? Justify your answer.
(d) The pipe can hold 50 cubic feet of water before overflowing. For t > 8, water continues to flow into and out of the pipe at the given rates until the pipe begins to overflow. Write, but do not solve, an equation involving one or more integrals that gives the time w when the pipe will begin to overflow.
▶️Answer/Explanation
Ans:
(a)
\(\int_{0}^{8}R(t)dt = \int_{0}^{8}20 sin\frac{t^{2}}{35}dt=76.570ft^{3}\)
During the eight hour interval, about 76.570 cubic feet of water flow into the drainpipe
(b)
Total water : T(x) \(T'(x) = R(x) – F(x) = 20in\frac{t^{2}}{35}+.04t.^{3}-.4t^{2}-.96t\)
T'(3) = 20 in 9/35 + .04(27) – .4(0) – .96(3) : : 314 < 0
after three hours, the amount of water in the pipe is decreasing because the derivative of the amount of water (the difference between water interring and leaving) is less than zero at 3 hours.
(c)
T'(t) = 0 @ t = 0, 3.2716584
\(T(t)=T(0)+\int_{0}^{t}T'(t)dt=30+\int_{0}^{t}T'(t)dt\)
T(0) = 30
T(3.272) = 27.965
T(8) = 48.544
after testing all critical numbers and endpoints for their values, the amount of water in the pipe achieves a minimum value of about 27.965 after about 3.272 hours.
(d)
50 = T(w)
\(50 = 30+\int_{0}^{w}T'(t)dt\)
\(20 = \int_{0}^{w}T'(t)dt=\int_{0}^{w}\left [ R(t)-D(t) \right ]dt\)
Question:
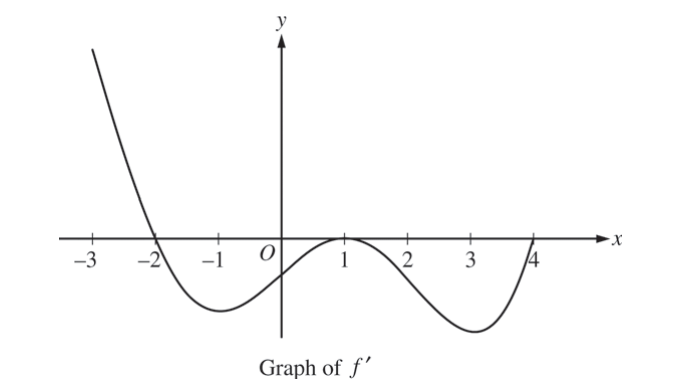
The figure above shows the graph of f’, the derivative of a twice-differentiable function f, on the interval [-3, 4] . The graph of f’ has horizontal tangents at x =- 1, x =1, and x = 3. The areas of the regions bounded by the x-axis and the graph of f’ on the intervals [-2, 1] and [1, 4] are 9 and 12, respectively.
(a) Find all x-coordinates at which f has a relative maximum. Give a reason for your answer.
(b) On what open intervals contained in -3 < x < 4 is the graph of f both concave down and decreasing? Give a reason for your answer.
(c) Find the x-coordinates of all points of inflection for the graph of f. Give a reason for your answer.
(d) Given that f(1) = 3,, write an expression for f(x) that involves an integral. Find f(4) and f(-2).
▶️Answer/Explanation
Ans:
(a)
∴ f(x) has a relative maximum at x = -2 because f'(x) switches from positive to negative of this point.
(b) The graph of f is both concave down and decreasing on the intervals (-2, -1) and (1, 3) because on these intervals f'(x) is negative and also f”(x) is negative.
(c)
x = -1, 1, 3
The x – coordinates of the points of inflection for the graph off f are x = -1, x = 1, x = 3, This is because at these points, f”(x) switches signs.
(d)
\(f(x)=\int_{1}^{x}f'(t)dt+3\)
\(f(4)=\int_{1}^{(4)}f'(t)dt+3\) \(f(-2)=\int_{1}^{(-2)}f'(t)dt+3\)
= (12) + 3 = (9) + 3
f(4) = -9 f(-2) = 12
Question:
When a certain grocery store opens, it has 50 pounds of bananas on a display table. Customers remove bananas from the display table at a rate modeled by
\(f(t)=10+(0.8t)sin\left ( \frac{t^{3}}{100} \right )\) for 0 < t ≤ 12,
where f ( t) is measured in pounds per hour and t is the number of hours after the store opened. After the store has been open for three hours, store employees add bananas to the display table at a rate modeled by
g(t) = 3 + 2.4 In (t2 + 2t) for 3 < t ≤ 12,
where g (t) is measured in pounds per hour and t is the number of hours after the store opened.
(a) How many pounds of bananas are removed from the display table during the first 2 hours the store is open?
(b) Find f'(7) . Using correct units, explain the meaning of f'(7) in the context of the problem.
(c) Is the number of pounds of bananas on the display table increasing or decreasing at time t = 5 ? Give a reason for your answer.
(d) How many pounds of bananas are on the display table at time t = 8 ?
▶️Answer/Explanation
Ans:
(a)
\(\int_{0}^{2}f(t)dt = 20.051\) lbs.
(b)
f'(7) = -8.119 lbs. per hour2
At time t = 7, the rate at which customers remove bananas from the display table is decreasing at a rate of 8.119 lbs. per hour per hour.
(c)
f(5) = 13.796
g(5) = 11.532
The number of pounds of bananas on the display table is decreasing at time t = 5, because f(5) > g(5).
(d)
\(50 – \int_{0}^{8}f(t)dt+\int_{3}^{8}g(t)dt=23.347\) lbs.
Question:
People enter a line for an escalator at a rate modeled by the function r given by
\(r(t)=\left\{\begin{matrix}
44\left ( \frac{t}{100} \right )^{3} \left ( 1-\frac{t}{300} \right )^{7}& for 0\leq t\leq 300 & \\
0&for t>300, &
\end{matrix}\right.\)
where r (t) is measured in people per second and t is measured in seconds. As people get on the escalator, they exit the line at a constant rate of 0.7 person per second. There are 20 people in line at time t = 0.
(a) How many people enter the line for the escalator during the time interval 0 ≤ t ≤ 300 ?
(b) During the time interval 0 ≤ t ≤ 300, there are always people in line for the escalator. How many people are in line at time t = 300 ?
(c) For t > 300, what is the first time t that there are no people in line for the escalator?
(d) For 0 ≤ t ≤ 300, at what time t is the number of people in line a minimum? To the nearest whole number, find the number of people in line at this time. Justify your answer.
▶️Answer/Explanation
Ans:
(a)
\(\int_{0}^{300}44\left ( \frac{t}{100} \right )^{3}\left ( 1-\frac{t}{300} \right )^{7}dt = 270\)
(b)
.7(300) = 210
20 + 270 = 290 290 – 210 = 80
(c)
(t-300)(.7) – 80 = 0
.7t – 210 – 80 = 0
.7t = +290
t = 414.2865
(d)
p = total people
\(\frac{dp}{dt}=r(t)-.7\)
0 = r(t) – .7
t = 166.575
t = 33.013
\(p(t)= \int_{0}^{6}r(x)-.7 dx + 20\)
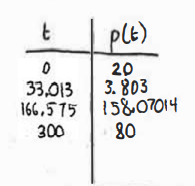
minimum at time t = 33.013 s when 4 people are in line
