AP Calculus AB 8.7 Volumes with Cross Sections: Squares and Rectangles- FRQs - Exam Style Questions
Calc-Ok Question
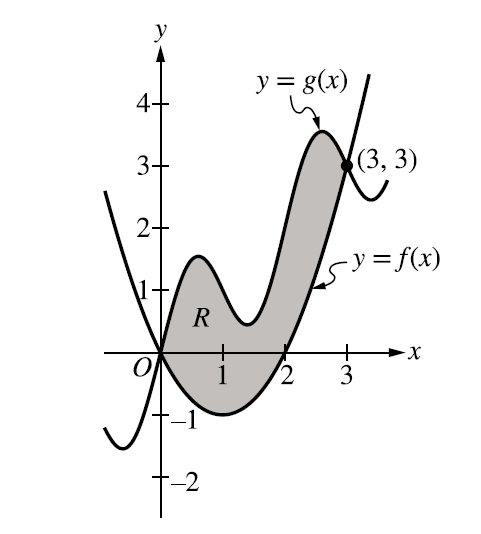
The shaded region \(R\) is bounded by the graphs of the functions \(f\) and \(g\), where \(f(x)=x^{2}-2x\) and \(g(x)=x+\sin(\pi x)\), as shown in the figure.
Most-appropriate topic codes (CED):
• TOPIC 8.7: Volumes with Cross Sections: Squares and Rectangles — part (B)
• TOPIC 8.12: Volume with Washer Method: Revolving Around Other Axes — part (C)
• TOPIC 2.2: Defining the Derivative and Using Derivative Notation (derivative as slope of the tangent line) — part (D)
▶️ Answer/Explanation
(A) Area of \(R\)
Intersections occur at \(x=0\) and \(x=3\) (since \(f(0)=g(0)=0\) and \(f(3)=g(3)=3\)). On \([0,3]\), the top curve is \(g\) and the bottom curve is \(f\).
\(\displaystyle \text{Area}=\int_{0}^{3}\!\big(g(x)-f(x)\big)\,dx=\int_{0}^{3}\!\big(x+\sin(\pi x)-(x^{2}-2x)\big)\,dx\)
\(\displaystyle =\int_{0}^{3}\!\big(-x^{2}+3x+\sin(\pi x)\big)\,dx\)
Antiderivative:
\(\displaystyle \int -x^{2}\,dx=-\frac{x^{3}}{3},\quad \int 3x\,dx=\frac{3x^{2}}{2},\quad \int \sin(\pi x)\,dx=-\frac{\cos(\pi x)}{\pi}.\)
Evaluate from \(0\) to \(3\):
\(\displaystyle \left[-\frac{x^{3}}{3}+\frac{3x^{2}}{2}-\frac{\cos(\pi x)}{\pi}\right]_{0}^{3}=\left(-9+\frac{27}{2}+\frac{1}{\pi}\right)-\left(0+0-\frac{1}{\pi}\right)\)
\(\displaystyle =\frac{9}{2}+\frac{2}{\pi}\approx 4.5+0.636619=\boxed{5.137}\ \text{(to 3 d.p.)}.\)
(B) Volume of solid with rectangular cross sections (height \(x\))
Cross-sectional area at \(x\): \(\displaystyle A(x)=\big(\text{base}\big)\times \big(\text{height}\big)=(g(x)-f(x))\times x.\)
\(\displaystyle A(x)=x\big(-x^{2}+3x+\sin(\pi x)\big)=-x^{3}+3x^{2}+x\sin(\pi x).\)
Volume:
\(\displaystyle V=\int_{0}^{3}\!A(x)\,dx=\int_{0}^{3}\!\big(-x^{3}+3x^{2}+x\sin(\pi x)\big)\,dx.\)
Compute each part:
\(\displaystyle \int_{0}^{3}\!-x^{3}\,dx=\left[-\frac{x^{4}}{4}\right]_{0}^{3}=-\frac{81}{4},\qquad \int_{0}^{3}3x^{2}\,dx=\left[x^{3}\right]_{0}^{3}=27.\)
For \(\displaystyle \int_{0}^{3} x\sin(\pi x)\,dx\), use integration by parts with \(u=x,\; dv=\sin(\pi x)dx\):
\(du=dx,\; v=-\dfrac{\cos(\pi x)}{\pi}\Rightarrow \int x\sin(\pi x)\,dx=-\dfrac{x\cos(\pi x)}{\pi}+\dfrac{\sin(\pi x)}{\pi^{2}}.\)
Evaluate \(0\) to \(3\): \(\displaystyle \left[-\frac{x\cos(\pi x)}{\pi}+\frac{\sin(\pi x)}{\pi^{2}}\right]_{0}^{3}=\frac{3}{\pi}.\)
Sum: \(\displaystyle V=\left(-\frac{81}{4}+27\right)+\frac{3}{\pi}=\frac{27}{4}+\frac{3}{\pi}=\boxed{\frac{12+27\pi}{4\pi}\approx 7.705}.\)
(C) Volume when \(R\) is rotated about \(y=-2\)
Use washers. Outer radius \(R(x)=g(x)-(-2)=g(x)+2\). Inner radius \(r(x)=f(x)-(-2)=f(x)+2\).
\(\displaystyle \text{Volume}=\pi\int_{0}^{3}\!\Big(\big(R(x)\big)^{2}-\big(r(x)\big)^{2}\Big)\,dx=\pi\int_{0}^{3}\!\Big((g(x)+2)^{2}-(f(x)+2)^{2}\Big)\,dx.\) (Do not evaluate.)
(D) Parallel tangents for \(0<x<1\)
Tangent lines are parallel \(\iff\) slopes are equal: \(f'(x)=g'(x)\). Here \(f'(x)=2x-2\) and \(g'(x)=1+\pi\cos(\pi x)\).
Solve \(\displaystyle 2x-2=1+\pi\cos(\pi x)\;\Rightarrow\; 2x-3=\pi\cos(\pi x).\)
Define \(h(x)=2x-3-\pi\cos(\pi x)\). Bracket the root:
\(h(0.60)\approx -1.800+0.971=-0.829<0,\quad h(0.70)\approx -1.600+1.848=0.248>0\Rightarrow\) root in \((0.60,0.70)\).
One Newton step from \(x_{0}=0.68\): \(h'(x)=2+\pi^{2}\sin(\pi x)\) so \(h'(0.68)\approx 2+9.8696\times 0.845\approx 10.342\).
\(h(0.68)\approx 0.057\Rightarrow x_{1}=x_{0}-\dfrac{h(0.68)}{h'(0.68)}\approx 0.68-\dfrac{0.057}{10.342}\approx 0.6745.\)
Refining (calculator, radians) gives \(\boxed{x\approx 0.675819}\) (acceptable to three decimals: \(x\approx 0.676\)).
