Question:
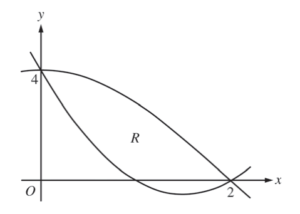
Let R be the region in the first quadrant bounded by the x-axis and the graphs of y = ln x and y = 5 – x, as shown in the figure above.
(a) Find the area of R.
(b) Region R is the base of a solid. For the solid, each cross section perpendicular to the x-axis is a square. Write, but do not evaluate, an expression involving one or more integrals that gives the volume of the solid.
(c) The horizontal line y = k divides R into two regions of equal area. Write, but do not solve, an equation involving one or more integrals whose solution gives the value of k.
▶️Answer/Explanation
Ans:
(a)
ey = x x = 5- y
1.307
\(A = \int_{0}^{1.307}(5-y-e^{y})dy\)
= 2.986
(b)
\(V = \int_{1}^{3.693}(In x)^{-2}dx +\int_{3.693}^{5}(5-x)^{-2}dx\)
(c)
\(V = \int_{0}^{k}(5-y-e^{y})dy =\int_{k}^{1.307}(5-y-e^{y})dy\)
Question:
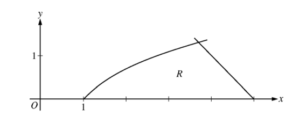
Let \(f(x)= 2x^{2}-6x+4\) and \(g(x)= 4 cos \left ( \frac{1}{4}\pi x \right ).\) Let R be the region bounded by the graphs of f and g, as shown in the figure above.
(a) Find the area of R.
(b) Write, but do not evaluate, an integral expression that gives the volume of the solid generated when R is rotated about the horizontal line y = 4.
(c) The region R is the base of a solid. For this solid, each cross section perpendicular to the x-axis is a square.
Write, but do not evaluate, an integral expression that gives the volume of the solid.
▶️Answer/Explanation
Ans:
(a)
\(R = \int_{0}^{2}\left ( 4 cos (\frac{1}{4}\pi x) -(2x^{2}-6x-4)\right )dx\)
\(R = \left ( \frac{16}{\pi } sin(\frac{1}{4}\pi x)-\frac{2}{3x^{3}}+3x^{2}-4x\right )_{0}^{2}\)
\(R = \left ( \frac{16}{\pi } sin(\frac{1}{2}\pi)-\frac{16}{3}+13-8\right )-\left ( \frac{16}{\pi } sin(0)-0+0-0\right )\)
\(R = \frac{16}{\pi }(1)-\frac{16}{3}+4\)
\(R = \frac{16}{\pi }-\frac{4}{3}\)
(b)
\(v = \pi \int_{0}^{2}\left ( 4-(2x^{2}-6x)+4 \right )^{2}-\left ( 4-4cos(\frac{1}{4}\pi x)\right )^{2}dx\)
\(v = \pi \int_{0}^{20}\left ( 2x^{2}+6x \right )^{2}-\left ( 4-4cos(\frac{1}{7}\pi x)\right )^{2}dx\)
(c)
\(v = \int_{0}^{2}\left ( 4cos(\frac{1}{4}\pi x)-( 2x^{2}-6x+4)\right )^{2}dx\)
\(v = \int_{0}^{2}\left ( 4cos(\frac{1}{4}\pi x)-( 2x^{2}+6x-4)\right )^{2}dx\)
Question:
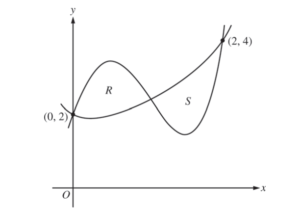
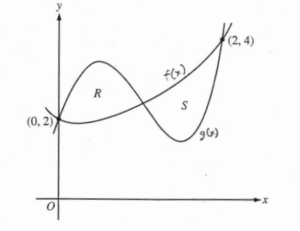
Let f and g be the functions defined by \(f(x)= 1 + x + e^{x^{2}-2x}\) and g(x) = x4 – 6.5x2 + 6x + 2. Let R and S be the two regions enclosed by the graphs of f and g shown in the figure above.
(a) Find the sum of the areas of regions R and S.
(b) Region S is the base of a solid whose cross sections perpendicular to the x-axis are squares. Find the volume of the solid.
(c) Let h be the vertical distance between the graphs of f and g in region S. Find the rate at which h changes with respect to x when x = 1.8.
▶️Answer/Explanation
Ans:
(a)
f(a) = g(a)
a = 1.0328318883641
\(\int_{0}^{9}\left [ g(x)-f(x) \right ]dx+\int_{0}^{2}\left [ f(x)-g(x) \right ]dx=2.004\)
(b)
Cross sation area A(x) = (f(x) – g(x))2 a = 1.0328318883641
\(\int_{2}^{9}A(x)dx=1.283\)
(c)
f'(1.8) = 2.1162821217136
g'(1.8) = 5.928
\(\frac{dh}{dx}=f'(1.8)-g'(1.8)=-3.812\)
Question:
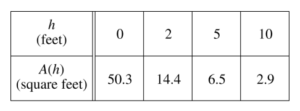
A tank has a height of 10 feet. The area of the horizontal cross section of the tank at height h feet is given by the function A, where A (h) is measured in square feet. The function A is continuous and decreases as h increases. Selected values for A (h) are given in the table above.
(a) Use a left Riemann sum with the three subintervals indicated by the data in the table to approximate the volume of the tank. Indicate units of measure.
(b) Does the approximation in part (a) overestimate or underestimate the volume of the tank? Explain your reasoning.
(c) The area, in square feet, of the horizontal cross section at height h feet is modeled by the function f given by \(f(h)=\frac{50.3}{e^{0.2h}+h}\) Based on this model, find the volume of the tank. Indicate units of measure.
(d) Water is pumped into the tank. When the height of the water is 5 feet, the height is increasing at the rate of 0.26 foot per minute. Using the model from part (c), find the rate at which the volume of water is changing with respect to time when the height of the water is 5 feet. Indicate units of measure.
▶️Answer/Explanation
Ans:
(a)
v ≈ [2(50.3) + 3 (14.4) + 5(6.5)]
≈ 176.3 ft3
(b)
The approximation in part a is an overestimate because A is a decreasing function.
(c)
\(v=\int_{0}^{10}\left ( \frac{50.3}{e^{0.2h}+h} \right )dh\)
≈ 101.325 ft3
(d)
h = 5 ft
\(\frac{dh}{dt}= 0.26 ft/min\)
\(\frac{dv}{dt}= ?\)
\(v=\int_{0}^{h}\left ( \frac{50.3}{e^{0.2h}+h} \right )dh\)
\(\frac{dv}{dt}= \frac{50.3}{e^{0.2h}+h}\cdot \frac{dh}{dt}\)
\( =\frac{50.3}{e^{0.2(5)}+(5)}\cdot 0.26\)
≈ 1.694 ft3/min
Question:
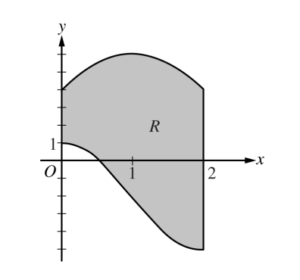
Let R be the region enclosed by the graphs of \(g(x)= -2 + 3 cos \left ( \frac{\pi }{2}x \right )\) and h(x) = 6 – 2(x-1)2, the y-axis, and the vertical line x = 2, as shown in the figure above.
(a) Find the area of R.
(b) Region R is the base of a solid. For the solid, at each x the cross section perpendicular to the x-axis has area \(A(x)=\frac{1}{x+3}.\) Find the volume of the solid.
(c) Write, but do not evaluate, an integral expression that gives the volume of the solid generated when R is rotated about the horizontal line y = 6.
▶️Answer/Explanation
Ans:
(a)
\(Area = \int_{0}^{2}h(x)-g(x)dx\)
\( = \int_{0}^{2}6-2(x-1)^{2}dx – \int_{0}^{2}-2+3 cos (\frac{\pi }{2}x)dx\)
\(=6x – \frac{2}{3}(x-1)^{3}|_{0}^{2}-\left ( -2x+\frac{6}{\pi }sin(\frac{\pi }{2}x) \right )|_{0}^{2}\)
\(=\left ( \left [ 12-\frac{2}{3}(1) \right ]-\left [ 0+\frac{2}{3} \right ] \right )-\left ( \left [ -4+\frac{6}{\pi }(0) \right ]-\left [ 0+0 \right ] \right )\)
\(=12-\frac{4}{3}+4=16-\frac{4}{3}\)
(b)
\(v = \int_{0}^{2}A(x)2x=\int_{0}^{2}\frac{1}{x+3}dx=ln|x+3||_{0}^{2}=ln |5| – ln |3|\)
= ln 5- ln 3
(c)
\(v = \int_{0}^{2}\pi \left [ (4-g(x))^{2}-(6-h(x))^{2} \right ]dx\)