AP Calculus AB 8.7 Volumes with Cross Sections: Squares and Rectangles - MCQs - Exam Style Questions
No-Calc Question
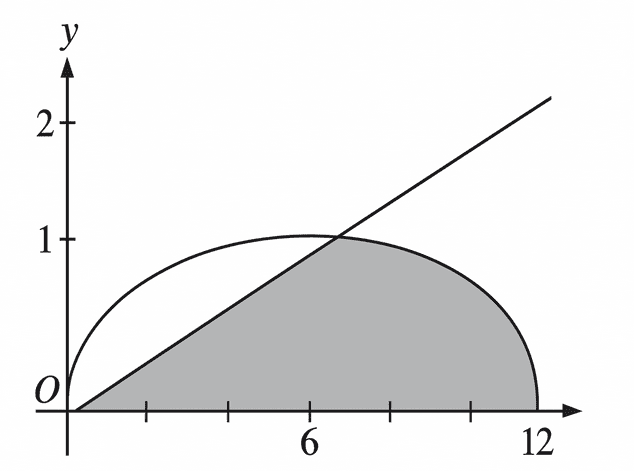
The base of a solid is the shaded region in the first quadrant bounded by the graphs of \(y=\sqrt{\sin\!\left(\dfrac{\pi x}{12}\right)}\) and \(y=\dfrac{1}{6}x\), as shown in the figure. For the solid, each cross section perpendicular to the \(x\)-axis is a square. Which of the following gives the volume of the solid?
(A) \(\displaystyle \int_{0}^{6}\frac{1}{36}x^{2}\,dx+\int_{6}^{12}\sin\!\left(\frac{\pi x}{12}\right)\,dx\)
(B) \(\displaystyle \pi\int_{0}^{6}\frac{1}{36}x^{2}\,dx+\pi\int_{6}^{12}\sin\!\left(\frac{\pi x}{12}\right)\,dx\)
(C) \(\displaystyle \int_{0}^{12}\!\left(\sqrt{\sin\!\left(\frac{\pi x}{12}\right)}-\frac{1}{6}x\right)^{2}\!dx\)
(D) \(\displaystyle \pi\int_{0}^{12}\!\left(\sqrt{\sin\!\left(\frac{\pi x}{12}\right)}-\frac{1}{6}x\right)^{2}\!dx\)
▶️ Answer/Explanation
Cross sections are squares, so area \(= (\text{side})^{2}\).
For \(0\le x\le 6\): top curve is \(y=\dfrac{1}{6}x\) ⇒ side \(=\dfrac{x}{6}\) ⇒ area \(=\left(\dfrac{x}{6}\right)^{2}=\dfrac{x^{2}}{36}\).
For \(6\le x\le 12\): top curve is \(y=\sqrt{\sin\!\left(\dfrac{\pi x}{12}\right)}\) ⇒ area \(=\sin\!\left(\dfrac{\pi x}{12}\right)\).
Volume is sum of areas over the two intervals.
✅ Answer: (A)
No-Calc Question
(B) \(\tfrac12 e^{2}-\tfrac12\)
(C) \(e^{2}-1\)
(D) \(2e^{2}-2\)
▶️ Answer/Explanation
Cross-sectional area \(A(x)=(e^{x})^{2}=e^{2x}\).
Volume \(\displaystyle V=\int_{0}^{1} e^{2x}\,dx=\Big[\tfrac12 e^{2x}\Big]_{0}^{1}=\tfrac12(e^{2}-1)\).
✅ Answer: (B)
