AP Calculus BC 1.7 Selecting Procedures for Determining Limits Study Notes - New Syllabus
AP Calculus BC 1.7 Selecting Procedures for Determining Limits Study Notes- New syllabus
AP Calculus BC 1.7 Selecting Procedures for Determining Limits Study Notes – AP Calculus BC- per latest AP Calculus BC Syllabus.
LEARNING OBJECTIVE
Reasoning with definitions, theorems, and properties can be used to justify claims about limits.
Key Concepts:
- Selecting Procedures for Determining Limits
Selecting Procedures for Determining Limits
Selecting Procedures for Determining Limits
In Calculus, different techniques are available to compute limits. The key skill is knowing which procedure to apply based on the given expression and its behavior.
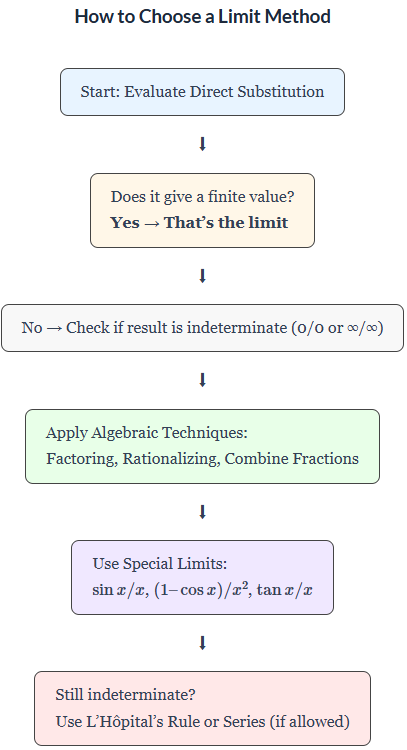
Strategy for Selecting Procedures:
- Start with Direct Substitution: If the function is continuous at the point, plug in the value directly.
- Check for Indeterminate Forms: If you get \( \frac{0}{0} \), \( \frac{\infty}{\infty} \), or similar, apply algebraic manipulation or special techniques.
- Use Algebraic Manipulation:
- Factor and simplify
- Multiply by conjugate (for radicals)
- Combine fractions
- Apply Special Limits:
- \( \lim_{x \to 0} \frac{\sin x}{x} = 1 \)
- \( \lim_{x \to 0} \frac{1 – \cos x}{x^2} = \frac{1}{2} \)
- \( \lim_{x \to 0} \frac{\tan x}{x} = 1 \)
- Use L’Hôpital’s Rule: For indeterminate forms after simplification, if allowed.
- Numerical or Graphical Estimation: If the limit is complicated, use a table or graph for approximation.
- Consider One-Sided Limits and Infinity: For limits at asymptotes or piecewise functions
Example :
Determine \( \lim_{x \to 2} (3x^2 – 4x + 5) \).
▶️ Answer/Explanation
Check continuity: Polynomial → continuous everywhere.
Use direct substitution: \( 3(2^2) – 4(2) + 5 = 12 – 8 + 5 = 9 \).
Answer: \( 9 \).
Example :
Compute \( \lim_{x \to 3} \frac{x^2 – 9}{x – 3} \).
▶️ Answer/Explanation
Direct substitution: \( \frac{0}{0} \) → indeterminate.
Factor numerator: \( (x – 3)(x + 3) \).
Simplify: \( x + 3 \).
Take limit: \( 6 \).
Answer: \( 6 \).
Example :
Find \( \lim_{x \to 4} \frac{\sqrt{x} – 2}{x – 4} \).
▶️ Answer/Explanation
Direct substitution: \( 0/0 \).
Multiply by conjugate: \( \frac{\sqrt{x} + 2}{\sqrt{x} + 2} \).
Simplify: \( \frac{1}{\sqrt{x} + 2} \).
Take limit: \( 1/4 \).
Answer: \( \frac{1}{4} \).
Example :
Evaluate \( \lim_{x \to 0} \frac{\sin(2x)}{x} \).
▶️ Answer/Explanation
Rewrite: \( \frac{\sin(2x)}{x} = \frac{\sin(2x)}{2x} \cdot 2 \).
Use special limit: \( \lim_{u \to 0} \frac{\sin u}{u} = 1 \).
Answer = \( 2 \).
Example :
Compute \( \lim_{x \to \infty} \frac{3x^2 + 1}{5x^2 – 7} \).
▶️ Answer/Explanation
Divide numerator and denominator by \( x^2 \):
\( \frac{3 + \frac{1}{x^2}}{5 – \frac{7}{x^2}} \to \frac{3}{5} \).
Answer: \( \frac{3}{5} \).
Example:
Compute \( \lim_{x \to b} \dfrac{b – x}{\sqrt{x} – \sqrt{b}} \).
(A) \( -2\sqrt{b} \)
(B) \( -\sqrt{b} \)
(C) \( 2b \)
(D) \( \sqrt{b} \)
(E) \( 2\sqrt{b} \)
▶️ Answer/Explanation
As \( x \to b \): numerator \( b – b = 0 \), denominator \( \sqrt{b} – \sqrt{b} = 0 \), so form = \( \frac{0}{0} \).
Multiply numerator and denominator by \( \sqrt{x} + \sqrt{b} \):
\( \dfrac{b – x}{\sqrt{x} – \sqrt{b}} \cdot \dfrac{\sqrt{x} + \sqrt{b}}{\sqrt{x} + \sqrt{b}} = \dfrac{(b – x)(\sqrt{x} + \sqrt{b})}{x – b}. \)
\( \dfrac{-(x – b)(\sqrt{x} + \sqrt{b})}{x – b} = -(\sqrt{x} + \sqrt{b}). \)
\( \lim_{x \to b} -(\sqrt{x} + \sqrt{b}) = -( \sqrt{b} + \sqrt{b}) = -2\sqrt{b}. \)
Answer: (A) \( -2\sqrt{b} \).
