Home / AP calculus AB and BC concise summary notes / AP Calculus BC 10.13 Radius and Interval of Convergence of Power Series Study Notes

AP Calculus BC 10.13 Radius and Interval of Convergence of Power Series Study Notes - New Syllabus

AP Calculus BC 10.13 Radius and Interval of Convergence of Power Series Study Notes- New syllabus

AP Calculus BC 10.13 Radius and Interval of Convergence of Power Series Study Notes – AP Calculus BC-  per latest AP Calculus BC Syllabus.

LEARNING OBJECTIVE

  • Power series allow us to represent associated functions on an appropriate interval.

Key Concepts: 

  • Radius and Interval of Convergence of Power Series

AP Calculus BC-Concise Summary Notes- All Topics

AP Calculus BC Exam Questions MCQs and FRQs

Radius and Interval of Convergence of Power Series

Radius and Interval of Convergence of Power Series

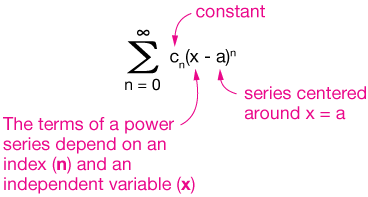
A power series centered at \( a \) is an infinite sum of the form:

$ \sum_{n=0}^{\infty} c_n (x-a)^n $

Here:

  • \( c_n \) = coefficient of the \( n \)th term.
  • \( a \) = center of the series.
  • \( x \) = variable.

A power series does not necessarily converge for all \( x \). The set of \( x \)-values for which it converges is called its interval of convergence.

Radius of Convergence (R):

 

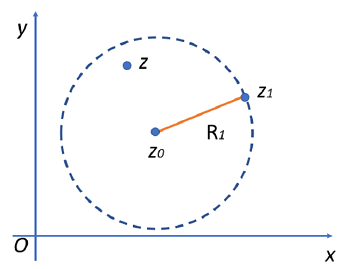
The radius of convergence \( R \) is a non-negative number (possibly \( 0 \) or \( \infty \)) such that:

  • The series converges absolutely when \( |x-a| < R \).
  • The series diverges when \( |x-a| > R \).
  • At the endpoints \( x = a \pm R \), the series may converge or diverge — these cases must be tested separately.

Finding the Radius and Interval of Convergence:

  • Step 1: Apply the Ratio Test or Root Test to the general term \( c_n (x-a)^n \).
  • Step 2: Solve the inequality \( L < 1 \) to find \( |x-a| < R \).
  • Step 3: Test the endpoints \( x = a – R \) and \( x = a + R \) individually to determine whether they should be included.
  • Step 4: Write the final interval of convergence.

Ratio Test Formula for Power Series:

$ L = \lim_{n \to \infty} \left| \dfrac{a_{n+1}}{a_n} \right| = |x-a| \cdot \lim_{n \to \infty} \left| \dfrac{c_{n+1}}{c_n} \right| $

If \( L < 1 \), the series converges absolutely.

Special Cases:

  • If \( R = 0 \), the series converges only at \( x = a \).
  • If \( R = \infty \), the series converges for all real \( x \).

Example

Find the radius and interval of convergence of the series: $ \sum_{n=1}^{\infty} \dfrac{(x-2)^n}{n \cdot 3^n} $

▶️ Answer/Explanation

Here \( c_n = \dfrac{1}{n \cdot 3^n} \).

Apply Ratio Test:

$ L = \lim_{n \to \infty} \left| \dfrac{ \frac{1}{(n+1)3^{n+1}} (x-2)^{n+1} }{ \frac{1}{n3^n} (x-2)^n } \right| = \lim_{n \to \infty} \left| \dfrac{n}{n+1} \cdot \dfrac{x-2}{3} \right| $

As \( n \to \infty \), \( \dfrac{n}{n+1} \to 1 \), so:

$ L = \left| \dfrac{x-2}{3} \right| $

Convergence if \( \left| \dfrac{x-2}{3} \right| < 1 \), which gives \( |x-2| < 3 \).

Radius: \( R = 3 \)

Preliminary interval: \( -1 < x < 5 \).

Test endpoints:

  • \( x = -1 \): Series becomes \( \sum \dfrac{(-3)^n}{n \cdot 3^n} = \sum \dfrac{(-1)^n}{n} \) → converges by Alternating Series Test.
  • \( x = 5 \): Series becomes \( \sum \dfrac{3^n}{n \cdot 3^n} = \sum \dfrac{1}{n} \) → diverges (harmonic series).

Final Interval: \( [-1, 5) \)

Example

Determine the radius and interval of convergence of: $ \sum_{n=0}^{\infty} \dfrac{(2x)^n}{n!} $

▶️ Answer/Explanation

Here \( c_n = \dfrac{2^n}{n!} \).

Ratio Test:

$ L = \lim_{n \to \infty} \left| \dfrac{ \frac{2^{n+1}}{(n+1)!} x^{n+1} }{ \frac{2^n}{n!} x^n } \right| = \lim_{n \to \infty} \left| \dfrac{2x}{n+1} \right| = 0 $

Since \( L = 0 \) for all \( x \), the series converges for all \( x \).

Radius: \( R = \infty \)

Interval: \( (-\infty, \infty) \)

Example

Consider the series: $ \sum_{n=1}^{\infty} \dfrac{(x+1)^n}{n^2 \cdot 4^n} $ Which of the following is the correct interval of convergence?

  1. \( (-5, 3] \)
  2. \( [-5, 3) \)
  3. \( [-5, 3] \)
  4. \( (-5, 3) \)
▶️ Answer/Explanation

Ratio Test:

$ L = \lim_{n \to \infty} \left| \dfrac{ \frac{1}{(n+1)^2 \cdot 4^{n+1}} (x+1)^{n+1} }{ \frac{1}{n^2 \cdot 4^n} (x+1)^n } \right| = \lim_{n \to \infty} \left| \dfrac{n^2}{(n+1)^2} \cdot \dfrac{x+1}{4} \right| $

As \( n \to \infty \), \( \dfrac{n^2}{(n+1)^2} \to 1 \), so:

$ L = \left| \dfrac{x+1}{4} \right| $

Convergence if \( |x+1| < 4 \) → \( -3 < x < 5 \).

Test endpoints:

  • \( x = -3 \): Term = \( \dfrac{(-2)^n}{n^2 \cdot 4^n} = \dfrac{(-1)^n}{n^2} \) → converges by p-series (\( p = 2 \)).
  • \( x = 5 \): Term = \( \dfrac{(6)^n}{n^2 \cdot 4^n} = \dfrac{(3/2)^n}{n^2} \) → diverges (ratio > 1).

Interval: \( [-3, 5) \)

Correct answer: B

Scroll to Top