AP Calculus BC 3.4 Differentiating Inverse Trigonometric Functions Study Notes - New Syllabus
AP Calculus BC 3.4 Differentiating Inverse Trigonometric Functions Study Notes- New syllabus
AP Calculus BC 3.4 Differentiating Inverse Trigonometric Functions Study Notes – AP Calculus BC- per latest AP Calculus BC Syllabus.
LEARNING OBJECTIVE
- Calculate derivatives of inverse trigonometric functions.
Key Concepts:
- Differentiating Inverse Trigonometric Functions
Differentiating Inverse Trigonometric Functions
Differentiating Inverse Trigonometric Functions
The derivative of an inverse trigonometric function can be calculated using standard formulas.
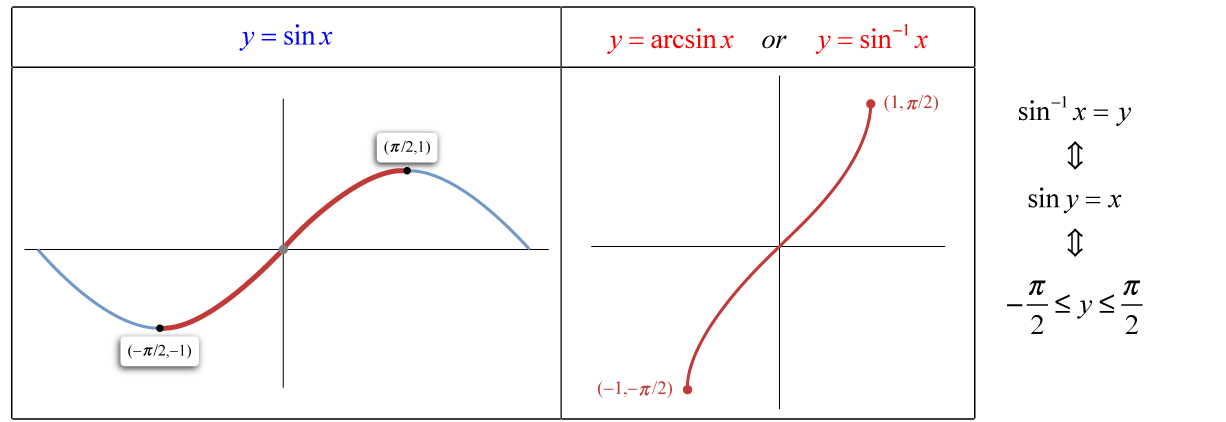
Graphs – Sin Vs. ArcSin
|
|---|
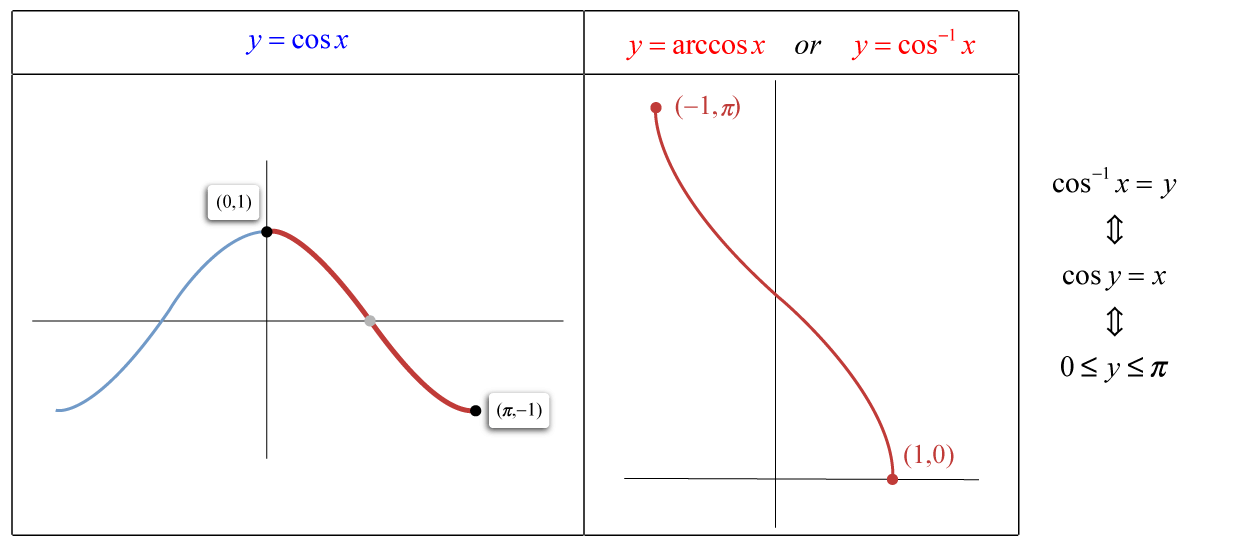
Graphs – Cos Vs. ArcCos
|
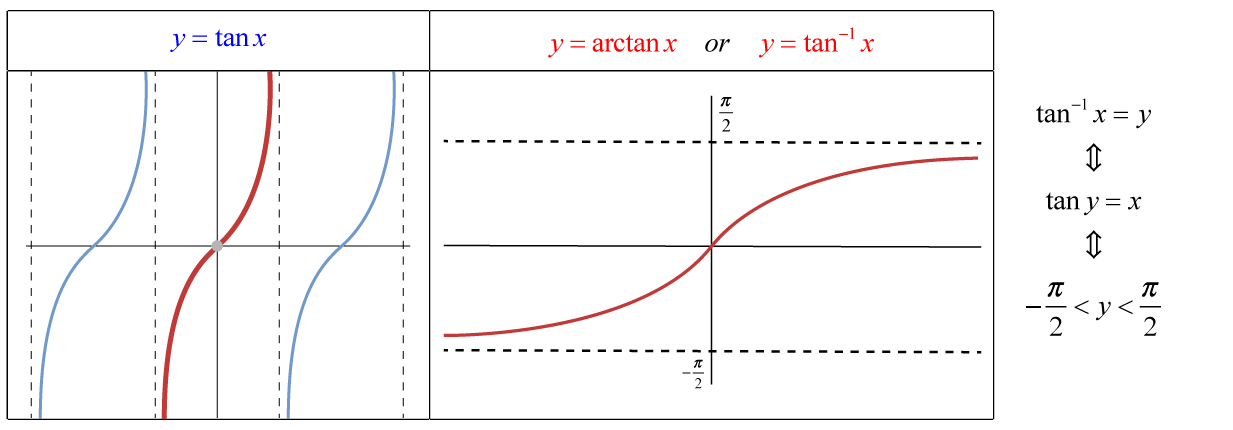
Graphs – Tan Vs. ArcTan
|
These functions are often encountered in calculus problems involving implicit differentiation, integration, and trigonometric identities.
Common Derivative Formulas:
| \( y \) | \( \dfrac{dy}{dx} \) |
|---|---|
| \( \sin^{-1}x \) | \( \dfrac{1}{\sqrt{1 – x^2}} \) |
| \( \cos^{-1}x \) | \( -\dfrac{1}{\sqrt{1 – x^2}} \) |
| \( \tan^{-1}x \) | \( \dfrac{1}{1 + x^2} \) |
| \( \cot^{-1}x \) | \( -\dfrac{1}{1 + x^2} \) |
| \( \sec^{-1}x \) | \( \dfrac{1}{|x|\sqrt{x^2 – 1}} \) |
| \( \csc^{-1}x \) | \( -\dfrac{1}{|x|\sqrt{x^2 – 1}} \) |
Differentiating Inverse Trigonometric Functions (with Chain Rule)
For composite functions involving inverse trig functions, use the Chain Rule:
\( \dfrac{d}{dx}[\text{inverse trig of }u] = (\text{derivative formula}) \cdot \dfrac{du}{dx} \).
| Function | Derivative |
|---|---|
| \( \sin^{-1}(f(x)) \) | \( \dfrac{f'(x)}{\sqrt{1 – (f(x))^2}} \) |
| \( \cos^{-1}(f(x)) \) | \( -\dfrac{f'(x)}{\sqrt{1 – (f(x))^2}} \) |
| \( \tan^{-1}(f(x)) \) | \( \dfrac{f'(x)}{1 + (f(x))^2} \) |
| \( \cot^{-1}(f(x)) \) | \( -\dfrac{f'(x)}{1 + (f(x))^2} \) |
| \( \sec^{-1}(f(x)) \) | \( \dfrac{f'(x)}{|f(x)|\sqrt{(f(x))^2 – 1}} \) |
| \( \csc^{-1}(f(x)) \) | \( -\dfrac{f'(x)}{|f(x)|\sqrt{(f(x))^2 – 1}} \) |
Example:
Find \( \dfrac{d}{dx}[\sin^{-1}(3x)] \).
▶️ Answer/Explanation
\( \dfrac{d}{dx}[\sin^{-1}(u)] = \dfrac{1}{\sqrt{1 – u^2}} \cdot u’ \).
Here \( u = 3x \), so \( u’ = 3 \).
\( \dfrac{dy}{dx} = \dfrac{3}{\sqrt{1 – (3x)^2}} = \dfrac{3}{\sqrt{1 – 9x^2}} \).
Answer: \( \dfrac{3}{\sqrt{1 – 9x^2}} \).
Example:
Find \( \dfrac{d}{dx}[\tan^{-1}(x^2)] \).
▶️ Answer/Explanation
\( \dfrac{d}{dx}[\tan^{-1}(u)] = \dfrac{1}{1+u^2} \cdot u’ \).
Here \( u = x^2 \), so \( u’ = 2x \).
\( \dfrac{dy}{dx} = \dfrac{2x}{1 + (x^2)^2} = \dfrac{2x}{1 + x^4} \).
Answer: \( \dfrac{2x}{1 + x^4} \).
Example:
If \( y = \cos^{-1}(\sqrt{x}) \), find \( \dfrac{dy}{dx} \).
▶️ Answer/Explanation
\( \dfrac{d}{dx}[\cos^{-1}(u)] = -\dfrac{1}{\sqrt{1 – u^2}} \cdot u’ \).
Here \( u = \sqrt{x} \), so \( u’ = \dfrac{1}{2\sqrt{x}} \).
\( \dfrac{dy}{dx} = -\dfrac{1}{\sqrt{1 – (\sqrt{x})^2}} \cdot \dfrac{1}{2\sqrt{x}} = -\dfrac{1}{2\sqrt{x(1 – x)}} \).
Answer: \( -\dfrac{1}{2\sqrt{x(1 – x)}} \).
Example:
Find \( \dfrac{d}{dx}[\sec^{-1}(2x)] \).
▶️ Answer/Explanation
\( \dfrac{d}{dx}[\sec^{-1}(u)] = \dfrac{1}{|u|\sqrt{u^2 – 1}} \cdot u’ \).
Here \( u = 2x \), so \( u’ = 2 \).
\( \dfrac{dy}{dx} = \dfrac{2}{|2x|\sqrt{(2x)^2 – 1}} = \dfrac{1}{|x|\sqrt{4x^2 – 1}} \).
Answer: \( \dfrac{1}{|x|\sqrt{4x^2 – 1}} \).
Example:
Find \( \dfrac{d}{dx}\big[\sin^{-1}(e^x)\big] \).
▶️ Answer/Explanation
\( \dfrac{d}{dx}[\sin^{-1}(u)] = \dfrac{1}{\sqrt{1 – u^2}} \cdot u’ \).
Here \( u = e^x \), so \( u’ = e^x \).
\( \dfrac{dy}{dx} = \dfrac{e^x}{\sqrt{1 – (e^x)^2}} = \dfrac{e^x}{\sqrt{1 – e^{2x}}} \).
Domain Note: For real derivative, \( x \le 0 \).
Answer: \( \dfrac{e^x}{\sqrt{1 – e^{2x}}}, \; x \le 0 \).