AP Calculus BC 6.12 Using Linear Partial Fractions Study Notes - New Syllabus
AP Calculus BC 6.12 Using Linear Partial Fractions Study Notes- New syllabus
AP Calculus BC 6.12 Using Linear Partial Fractions Study Notes – AP Calculus BC- per latest AP Calculus BC Syllabus.
LEARNING OBJECTIVE
- Recognizing opportunities to apply knowledge of geometry and mathematical rules can simplify integration.
Key Concepts:
- Integrating Using Linear Partial Fractions
Integrating Using Linear Partial Fractions
Integrating Using Linear Partial Fractions
Partial fractions help us integrate rational functions by breaking them into simpler fractions that are easier to integrate.
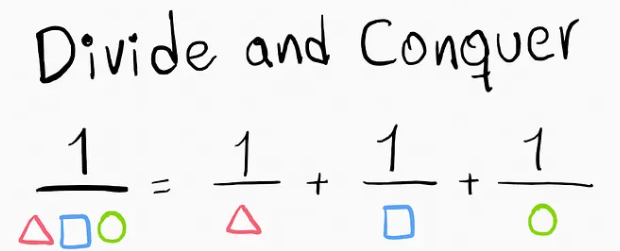
General Form: If you have a rational function \( \dfrac{P(x)}{Q(x)} \), where the degree of the numerator is less than the degree of the denominator, and \( Q(x) \) factors into linear or irreducible quadratic factors, you can decompose it into a sum of simpler fractions.
Types of Partial Fraction Decomposition
| Type of Denominator | Form of Decomposition |
|---|---|
| \( (x – a)(x – b) \) (Distinct linear factors) | \( \dfrac{A}{x – a} + \dfrac{B}{x – b} \) |
| \( (x – a)^n \) (Repeated linear factor) | \( \dfrac{A_1}{x – a} + \dfrac{A_2}{(x – a)^2} + \dots + \dfrac{A_n}{(x – a)^n} \) |
| \( x^2 + px + q \) (Irreducible quadratic factor) | \( \dfrac{Ax + B}{x^2 + px + q} \) |
| \( (x^2 + px + q)^n \) (Repeated irreducible quadratic) | \( \dfrac{A_1x + B_1}{x^2 + px + q} + \dfrac{A_2x + B_2}{(x^2 + px + q)^2} + \dots + \dfrac{A_nx + B_n}{(x^2 + px + q)^n} \) |
Example:
Find the integral: \(\displaystyle \int \dfrac{3x + 5}{(x + 1)(x + 2)} \, dx \)
▶️Answer/Explanation
Decompose: \( \dfrac{3x + 5}{(x + 1)(x + 2)} = \dfrac{A}{x + 1} + \dfrac{B}{x + 2} \)
Solving: \( 3x + 5 = A(x + 2) + B(x + 1) \Rightarrow A = 2, B = 1 \)
Integrate: \(\displaystyle \int \left( \dfrac{2}{x + 1} + \dfrac{1}{x + 2} \right) dx = 2\ln|x + 1| + \ln|x + 2| + C \)
Answer: \( \boxed{2\ln|x + 1| + \ln|x + 2| + C} \)
Example:
Evaluate: \(\displaystyle \int_1^2 \dfrac{5x + 4}{(x + 1)(x + 2)} \, dx \)
▶️Answer/Explanation
Decompose: \( \dfrac{5x + 4}{(x + 1)(x + 2)} = \dfrac{-1}{x + 1} + \dfrac{6}{x + 2} \)
Now integrate each: \( -\int_1^2 \dfrac{1}{x + 1} dx + 6\displaystyle \int_1^2 \dfrac{1}{x + 2} dx \)
Evaluate using logs: \( = -[\ln(x + 1)]_1^2 + 6[\ln(x + 2)]_1^2 \)
= \( \ln(2) – \ln(3) + 6(\ln(4) – \ln(3)) = \ln\left(\dfrac{2}{3}\right) + 6\ln\left(\dfrac{4}{3}\right) \)
Answer: \( \boxed{\ln\left( \dfrac{2}{3} \cdot \left( \dfrac{4}{3} \right)^6 \right)} \)
Example:
Find \(\displaystyle \int \dfrac{4x + 3}{(x – 1)^2} \, dx \)
▶️Answer/Explanation
Decompose: \( \dfrac{4x + 3}{(x – 1)^2} = \dfrac{A}{x – 1} + \dfrac{B}{(x – 1)^2} \)
Clear denominator: \( 4x + 3 = A(x – 1) + B \)
Let \( x = 1 \): \( 4(1) + 3 = A(0) + B \Rightarrow B = 7 \)
Now plug another value, say \( x = 0 \): \( 0 + 3 = A(-1) + 7 \Rightarrow A = 4 \)
Integrate: \(\displaystyle \int \left( \dfrac{4}{x – 1} + \dfrac{7}{(x – 1)^2} \right) dx = 4\ln|x – 1| – \dfrac{7}{x – 1} + C \)
Answer: \( \boxed{4\ln|x – 1| – \dfrac{7}{x – 1} + C} \)
Example:
Find \(\displaystyle \int \dfrac{3x + 2}{(x^2 + 1)(x – 1)} \, dx \)
▶️Answer/Explanation
We decompose: \( \dfrac{3x + 2}{(x^2 + 1)(x – 1)} = \dfrac{A}{x – 1} + \dfrac{Bx + C}{x^2 + 1} \)
Multiply both sides by \( (x – 1)(x^2 + 1) \): \( 3x + 2 = A(x^2 + 1) + (Bx + C)(x – 1) \)
Expand and group terms: \( 3x + 2 = A(x^2 + 1) + Bx(x – 1) + C(x – 1) \)
Now solve for A, B, C using values (or comparing coefficients). After solving: \( A = 1 \), \( B = 2 \), \( C = 2 \)
So the integrand becomes: \( \dfrac{1}{x – 1} + \dfrac{2x + 2}{x^2 + 1} \)
Now integrate: \(\displaystyle \int \dfrac{1}{x – 1} dx +\displaystyle \int \dfrac{2x}{x^2 + 1} dx +\displaystyle \int \dfrac{2}{x^2 + 1} dx \)
Results: \( \ln|x – 1| + \ln(x^2 + 1) + 2\arctan(x) + C \)
Answer: \( \boxed{\ln|x – 1| + \ln(x^2 + 1) + 2\arctan(x) + C} \)
Example:
Evaluate \(\displaystyle \int_0^1 \dfrac{x + 3}{x^2 + 4} \, dx \)
▶️Answer/Explanation
Break the fraction into parts: \( \dfrac{x + 3}{x^2 + 4} = \dfrac{x}{x^2 + 4} + \dfrac{3}{x^2 + 4} \)
Now integrate term-by-term: \(\displaystyle \int_0^1 \dfrac{x}{x^2 + 4} dx +\displaystyle \int_0^1 \dfrac{3}{x^2 + 4} dx \)
First term: Let \( u = x^2 + 4 \Rightarrow du = 2x dx \Rightarrow \dfrac{1}{2} du = x dx \) So,\displaystyle \int \dfrac{x}{x^2 + 4} dx = \dfrac{1}{2} \ln(x^2 + 4) \)
Second term: \(\displaystyle \int \dfrac{3}{x^2 + 4} dx = \dfrac{3}{2} \arctan\left(\dfrac{x}{2}\right) \)
Now apply limits \( x = 0 \) to \( x = 1 \):
\( = \left[ \dfrac{1}{2} \ln(x^2 + 4) + \dfrac{3}{2} \arctan\left(\dfrac{x}{2}\right) \right]_0^1\)
\( = \dfrac{1}{2} \ln(5) – \dfrac{1}{2} \ln(4) + \dfrac{3}{2} \left( \arctan\left(\dfrac{1}{2}\right) – \arctan(0) \right) \)
Answer: \( \boxed{\dfrac{1}{2} \ln\left(\dfrac{5}{4}\right) + \dfrac{3}{2} \arctan\left(\dfrac{1}{2}\right)} \)
