AP Calculus BC 6.13 Evaluating Improper Integrals Study Notes - New Syllabus
AP Calculus BC 6.13 Evaluating Improper Integrals Study Notes- New syllabus
AP Calculus BC 6.13 Evaluating Improper Integrals Study Notes – AP Calculus BC- per latest AP Calculus BC Syllabus.
LEARNING OBJECTIVE
- Upd
Key Concepts:
- Upd
Evaluating Improper Integrals
Evaluating Improper Integrals
An improper integral is a definite integral where either:
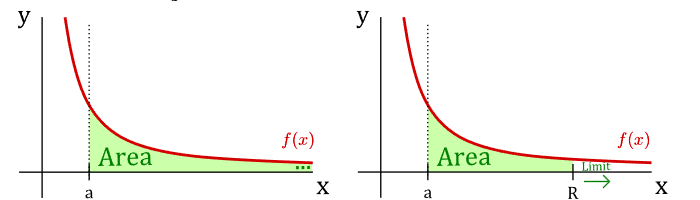
- One or both limits of integration are infinite, or
- The integrand becomes unbounded (infinite) within the interval of integration.
Such integrals are evaluated by taking limits of definite integrals.
General Method:
If the integral is improper, replace the infinite limit or the point of discontinuity with a variable, then take the limit of the definite integral as that variable approaches the problematic value.
Types of Improper Integrals:
| Case | Form | Limit Representation |
|---|---|---|
| Infinite upper limit | \( \displaystyle \int_a^{\infty} f(x) \, dx \) | \( \displaystyle \lim_{t \to \infty} \int_a^t f(x) \, dx \) |
| Infinite lower limit | \( \displaystyle \int_{-\infty}^b f(x) \, dx \) | \( \displaystyle \lim_{t \to -\infty} \int_t^b f(x) \, dx \) |
| Infinite limits on both sides | \( \displaystyle \int_{-\infty}^{\infty} f(x) \, dx \) | \( \displaystyle \lim_{p \to -\infty} \int_p^c f(x) \, dx + \lim_{q \to \infty} \int_c^q f(x) \, dx \) where \(c\) is any point between \(-\infty\) and \(\infty\). |
| Discontinuous at a limit | \( \displaystyle \int_a^b f(x) \, dx \) where \(f(x)\) is undefined at \(a\) or \(b\) | \( \displaystyle \lim_{t \to a^+} \int_t^b f(x) \, dx \) or \( \displaystyle \lim_{t \to b^-} \int_a^t f(x) \, dx \) |
| Discontinuous inside the interval | \( \displaystyle \int_a^b f(x) \, dx \) where \(f(x)\) is undefined at \(c\), \(a < c < b\) | \( \displaystyle \lim_{p \to c^-} \int_a^p f(x) \, dx + \lim_{q \to c^+} \int_q^b f(x) \, dx \) |
Example:
Evaluate \( \displaystyle \int_1^{\infty} \frac{1}{x^2} \, dx \).
▶️Answer/Explanation
We write: \( \displaystyle \int_1^{\infty} \frac{1}{x^2} dx = \lim_{t \to \infty} \int_1^t x^{-2} dx \) \( = \lim_{t \to \infty} \left[ -\dfrac{1}{x} \right]_1^t \)
\( = \lim_{t \to \infty} \left( -\dfrac{1}{t} + 1 \right) = 1 \)
Example:
Evaluate \( \displaystyle \int_{-\infty}^0 e^x \, dx \).
▶️Answer/Explanation
We write: \( \displaystyle \int_{-\infty}^0 e^x dx = \lim_{t \to -\infty} \int_t^0 e^x dx \)
\( = \lim_{t \to -\infty} \left[ e^x \right]_t^0 \)
\( = \lim_{t \to -\infty} \left( 1 – e^t \right) = 1 \)
Example:
Evaluate \( \displaystyle \int_{-\infty}^{\infty} e^{-x^2} \, dx \).
▶️Answer/Explanation
We write: \( \displaystyle \int_{-\infty}^{\infty} e^{-x^2} dx = \lim_{p \to -\infty} \displaystyle \int_p^0 e^{-x^2} dx + \lim_{q \to \infty} \displaystyle \int_0^q e^{-x^2} dx \)
The known Gaussian integral result is: \(\displaystyle \int_{-\infty}^{\infty} e^{-x^2} dx = \sqrt{\pi} \)
Example:
Evaluate \( \displaystyle \int_0^1 \frac{1}{\sqrt{x}} \, dx \).
▶️Answer/Explanation
We write: \( \displaystyle \int_0^1 \frac{1}{\sqrt{x}} dx = \lim_{t \to 0^+} \int_t^1 x^{-1/2} dx \) \( = \lim_{t \to 0^+} \left[ 2x^{1/2} \right]_t^1 \)
\( = \lim_{t \to 0^+} \left( 2 – 2\sqrt{t} \right) = 2 \)
Example:
Evaluate \( \displaystyle \int_0^2 \frac{1}{x – 1} \, dx \).
▶️Answer/Explanation
Here \(x = 1\) is a point of discontinuity inside the interval: \( \displaystyle \int_0^2 \frac{1}{x – 1} dx = \lim_{p \to 1^-}\displaystyle \int_0^p \frac{1}{x – 1} dx + \lim_{q \to 1^+} \displaystyle \int_q^2 \frac{1}{x – 1} dx \)
Both limits diverge to \( \pm\infty \), so the integral does not converge.
