AP Calculus BC 6.9 Integrating Using Substitution Study Notes - New Syllabus
AP Calculus BC 6.9 Integrating Using Substitution Study Notes- New syllabus
AP Calculus BC 6.9 Integrating Using Substitution Study Notes – AP Calculus BC- per latest AP Calculus BC Syllabus.
LEARNING OBJECTIVE
- Recognizing opportunities to apply knowledge of geometry and mathematical rules can simplify integration.
Key Concepts:
- Integrating Using Substitution
Integrating Using Substitution
Integrating Using Substitution
U-Substitution is a method for evaluating integrals and is essentially the reverse of the chain rule for differentiation. It helps simplify integrals where a composite function is involved.

If an integrand looks like a composition of functions (e.g., something of the form \( f(g(x))g'(x) \)), we let \( u = g(x) \). Then, \( du = g'(x)dx \), and the integral becomes easier in terms of \( u \).
Steps for Substitution:
- Identify an inner function \( u = g(x) \) such that its derivative \( g'(x) \) also appears in the integrand.
- Compute \( du = g'(x)dx \).
- Rewrite the entire integral in terms of \( u \) and \( du \).
- Integrate with respect to \( u \).
- Substitute back \( u = g(x) \) in the final answer.
Example:
Evaluate \(\displaystyle \int 2x(x^2 + 1)^5 \, dx \)
▶️Answer/Explanation
Let \( u = x^2 + 1 \Rightarrow du = 2x\,dx \)
The integral becomes: \(\displaystyle \int u^5 \, du = \dfrac{u^6}{6} + C \)
Substitute back: \( \dfrac{(x^2 + 1)^6}{6} + C \)
Example:
Evaluate \(\displaystyle \int \cos(3x)\,dx \)
▶️Answer/Explanation
Let \( u = 3x \Rightarrow du = 3dx \Rightarrow dx = \dfrac{1}{3}du \)
Integral becomes: \(\displaystyle \int \cos(u) \cdot \dfrac{1}{3}du = \dfrac{1}{3}\sin(u) + C \)
Substitute back: \( \dfrac{1}{3}\sin(3x) + C \)
Example:
Evaluate \(\displaystyle \int \dfrac{x}{\sqrt{x^2 + 4}} \, dx \)
▶️Answer/Explanation
Let \( u = x^2 + 4 \Rightarrow du = 2x\,dx \Rightarrow \dfrac{1}{2}du = x\,dx \)
Integral becomes: \(\displaystyle \int \dfrac{1}{\sqrt{u}} \cdot \dfrac{1}{2} du = \dfrac{1}{2}\displaystyle \int u^{-1/2} du \)
= \( \dfrac{1}{2} \cdot \dfrac{u^{1/2}}{1/2} = \sqrt{u} \)
Substitute back: \( \sqrt{x^2 + 4} + C \)
Example:
Evaluate \(\displaystyle \int \dfrac{1}{x \ln x}\,dx \)
▶️Answer/Explanation
Let \( u = \ln x \Rightarrow du = \dfrac{1}{x}dx \)
Integral becomes: \(\displaystyle \int \dfrac{1}{u} du = \ln|u| + C \)
Substitute back: \( \ln|\ln x| + C \)
Substitution in Definite Integrals
When applying \( u \)-substitution to a definite integral \(\displaystyle \int_a^b f(x)\,dx \), you must change both:
- The integrand rewrite it in terms of \( u \).
- The limits of integration convert \( x = a \) and \( x = b \) to corresponding \( u \)-values.
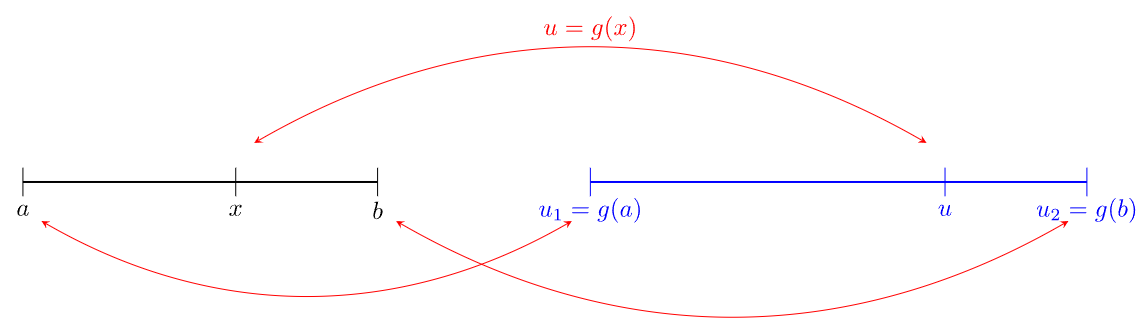
If \( u = g(x) \), then:
\(\displaystyle \int_a^b f(x)\,dx =\displaystyle \int_{u(a)}^{u(b)} f(g^{-1}(u)) \cdot \dfrac{dx}{du} \, du \)
In practice, you simplify: \(\displaystyle \int_a^b f(x)\,dx =\displaystyle \int_{u(a)}^{u(b)} f(u)\, du \)
Example:
Evaluate the definite integral: \(\displaystyle \int_0^2 x(x^2 + 1)^3 \, dx \)
▶️Answer/Explanation
Let \( u = x^2 + 1 \) ⇒ \( du = 2x\,dx \Rightarrow \dfrac{1}{2}du = x\,dx \)
Change the limits:
- When \( x = 0 \), \( u = 0^2 + 1 = 1 \)
- When \( x = 2 \), \( u = 2^2 + 1 = 5 \)
Rewrite the integral:
\(\displaystyle \int_0^2 x(x^2 + 1)^3\,dx =\displaystyle \int_1^5 u^3 \cdot \dfrac{1}{2} du = \dfrac{1}{2}\displaystyle \int_1^5 u^3\,du \)
Integrate:
\( \dfrac{1}{2} \cdot \left[ \dfrac{u^4}{4} \right]_1^5 = \dfrac{1}{2} \cdot \left( \dfrac{5^4}{4} – \dfrac{1^4}{4} \right) = \dfrac{1}{2} \cdot \left( \dfrac{625 – 1}{4} \right) = \dfrac{1}{2} \cdot \dfrac{624}{4} = \dfrac{624}{8} = 78 \)
Final Answer: \( \boxed{78} \)
Example:
Evaluate the definite integral: \(\displaystyle \int_0^{\ln 2} \dfrac{e^x}{1 + e^x}\, dx \)
▶️Answer/Explanation
Let \( u = 1 + e^x \) Then \( du = e^x\, dx \)
Change the limits of integration:
- When \( x = 0 \), \( u = 1 + e^0 = 2 \)
- When \( x = \ln 2 \), \( u = 1 + e^{\ln 2} = 1 + 2 = 3 \)
Rewrite the integral using substitution:
\(\displaystyle \int_0^{\ln 2} \dfrac{e^x}{1 + e^x}\, dx =\displaystyle \int_2^3 \dfrac{1}{u}\, du \)
Integrate:
\(\displaystyle \int_2^3 \dfrac{1}{u}\, du = \ln|u| \Big|_2^3 = \ln(3) – \ln(2) = \ln\left( \dfrac{3}{2} \right) \)
Final Answer: \( \boxed{\ln\left( \dfrac{3}{2} \right)} \)
