AP Calculus BC 8.8 Volumes with Cross Sections: Triangles and Semicircles Study Notes - New Syllabus
AP Calculus BC 8.8 Volumes with Cross Sections: Triangles and Semicircles Study Notes- New syllabus
AP Calculus BC 8.8 Volumes with Cross Sections: Triangles and Semicircles Study Notes – AP Calculus BC- per latest AP Calculus BC Syllabus.
LEARNING OBJECTIVE
- Definite integrals allow us to solve problems involving the accumulation of change over an interval.
Key Concepts:
- Volumes with Cross Sections: Triangles and Semicircles
Volumes with Cross Sections: Triangles and Semicircles
Volumes with Cross Sections : Triangles
When the base of a solid lies in the \( xy \)-plane and the cross sections perpendicular to the \( x \)-axis or \( y \)-axis are triangles, the volume can be calculated by integrating the area of each triangular cross section over the given interval.
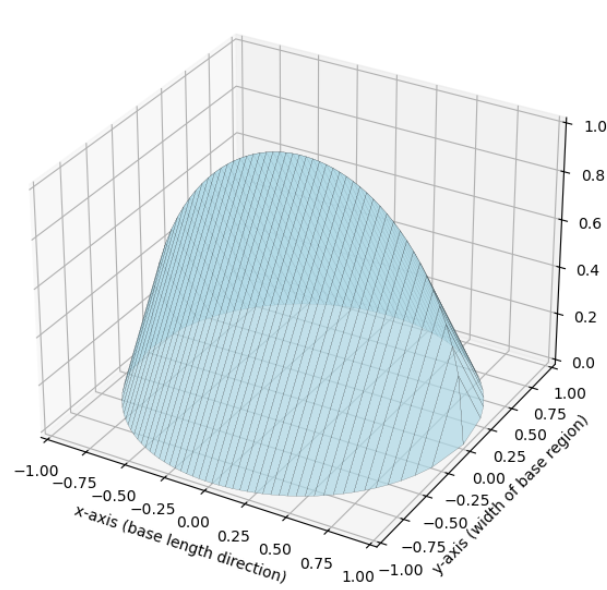
The base of each triangular cross section corresponds to the distance between the bounding curves in the plane. The height is related to the base by a constant factor \( k \), which depends on the type of triangle:
- For an equilateral triangle: \( h = \dfrac{\sqrt{3}}{2} \cdot \text{base} \)
- For a right isosceles triangle: \( h = \text{base} \)
- For a general triangle: \( h = k \cdot \text{base} \)
Since the area of a triangle is \( \dfrac{1}{2} (\text{base}) (\text{height}) \), we can write:
\( A(x) = \dfrac{1}{2} \cdot \left[ \text{Base Length} \right] \cdot \left[ k \cdot \text{Base Length} \right] = \dfrac{k}{2} \left[ \text{Base Length} \right]^2 \)
If cross sections are perpendicular to the \( x \)-axis:
\( V = \displaystyle \int_{a}^{b} \dfrac{k}{2} \left[ f(x) – g(x) \right]^2 \, dx \)
If cross sections are perpendicular to the \( y \)-axis:
\( V = \displaystyle \int_{c}^{d} \dfrac{k}{2} \left[ f(y) – g(y) \right]^2 \, dy \)
Example:
The base of a solid is bounded by \( y = \sqrt{x} \) and \( y = 0 \) for \( 0 \leq x \leq 4 \). Each cross section perpendicular to the \( x \)-axis is an equilateral triangle. Find the volume of the solid.
▶️ Answer/Explanation
The base length of a cross section is:
\( \text{Base Length} = \sqrt{x} – 0 = \sqrt{x} \)
For an equilateral triangle, \( h = \dfrac{\sqrt{3}}{2} \cdot \text{base} \), so:
\( A(x) = \dfrac{1}{2} \cdot \text{base} \cdot h = \dfrac{1}{2} \cdot \sqrt{x} \cdot \dfrac{\sqrt{3}}{2} \cdot \sqrt{x} \)
\( A(x) = \dfrac{\sqrt{3}}{4} \cdot x \)
Integrating along \( 0 \leq x \leq 4 \):
\( V = \displaystyle \int_{0}^{4} \dfrac{\sqrt{3}}{4} x \, dx = \dfrac{\sqrt{3}}{4} \cdot \left[ \dfrac{x^2}{2} \right]_{0}^{4} \)
\( V = \dfrac{\sqrt{3}}{4} \cdot \dfrac{16}{2} = 2\sqrt{3} \)
Final Answer: \( V = 2\sqrt{3} \ \text{units}^3 \)
Example:
The base of a solid is bounded by \( y = x \) and \( y = 0 \) for \( 0 \leq x \leq 2 \). Cross sections perpendicular to the \( x \)-axis are right isosceles triangles whose legs lie in the base.
▶️ Answer/Explanation
Base length: \( x – 0 = x \)
For a right isosceles triangle, \( h = \text{base} \), so:
\( A(x) = \dfrac{1}{2} \cdot x \cdot x = \dfrac{x^2}{2} \)
\( V = \displaystyle \int_{0}^{2} \dfrac{x^2}{2} \, dx = \dfrac{1}{2} \cdot \left[ \dfrac{x^3}{3} \right]_{0}^{2} = \dfrac{1}{2} \cdot \dfrac{8}{3} = \dfrac{4}{3} \)
Final Answer: \( V = \dfrac{4}{3} \ \text{units}^3 \)
Example:
The base of a solid is bounded by \( y = 2 \) and \( y = x \) for \( 0 \leq x \leq 2 \). Each cross section perpendicular to the \( x \)-axis is a triangle whose height is twice its base length.
▶️ Answer/Explanation
Base length: \( 2 – x \)
Height: \( h = 2 \cdot \text{base} = 2(2 – x) \)
Area: \( A(x) = \dfrac{1}{2} \cdot (2 – x) \cdot [2(2 – x)] = (2 – x)^2 \)
Volume: \( V = \displaystyle \int_{0}^{2} (2 – x)^2 \, dx \)
Expand: \( (2 – x)^2 = 4 – 4x + x^2 \)
\( V = \left[ 4x – 2x^2 + \dfrac{x^3}{3} \right]_{0}^{2} = \left[ 8 – 8 + \dfrac{8}{3} \right] – 0 = \dfrac{8}{3} \)
Final Answer: \( V = \dfrac{8}{3} \ \text{units}^3 \)
Volumes with Cross Sections: Semi-circles
When the base of a solid lies in the \( xy \)-plane and cross sections perpendicular to the \( x \)-axis (or \( y \)-axis) are semi-circles, the volume can be determined by integrating the area of each semi-circular cross section along the given interval.
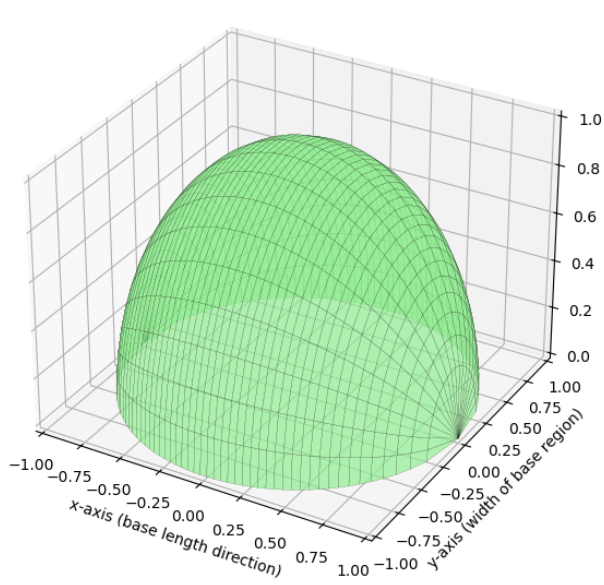
If the diameter of each semi-circle is the distance between the bounding curves \( f(x) \) and \( g(x) \), then:
Diameter: \( D = f(x) – g(x) \)
Radius: \( r = \dfrac{D}{2} \)
Area of semi-circle: \( A(x) = \dfrac{1}{2} \pi r^{2} = \dfrac{1}{2} \pi \left( \dfrac{f(x) – g(x)}{2} \right)^{2} \)
For perpendicular cross sections to the \( x \)-axis:
\( V = \displaystyle \int_{a}^{b} \dfrac{\pi}{8} \left[ f(x) – g(x) \right]^{2} \, dx \)
For perpendicular cross sections to the \( y \)-axis:
\( V = \displaystyle \int_{c}^{d} \dfrac{\pi}{8} \left[ f(y) – g(y) \right]^{2} \, dy \)
Example:
The base of a solid is bounded by \( y = \sqrt{x} \) and \( y = 0 \) for \( 0 \leq x \leq 4 \). Each cross section perpendicular to the \( x \)-axis is a semi-circle whose diameter is the distance between the curves. Find the volume of the solid.
▶️ Answer/Explanation
Here, the diameter is \( D = \sqrt{x} – 0 = \sqrt{x} \). Radius: \( r = \dfrac{\sqrt{x}}{2} \) Area of each cross section: \( A(x) = \dfrac{1}{2} \pi \left( \dfrac{\sqrt{x}}{2} \right)^{2} = \dfrac{\pi x}{8} \)
Volume: \( V = \displaystyle \int_{0}^{4} \dfrac{\pi x}{8} \, dx = \dfrac{\pi}{8} \left[ \dfrac{x^{2}}{2} \right]_{0}^{4} = \dfrac{\pi}{8} \cdot \dfrac{16}{2} = \dfrac{\pi}{8} \cdot 8 = \pi \)
Final Answer: \( V = \pi \)
Example:
The base of a solid is bounded by \( x = 4 – y^{2} \) and \( x = 0 \) for \( -2 \leq y \leq 2 \). Each cross section perpendicular to the \( y \)-axis is a semi-circle whose diameter is the distance between the curves. Find the volume of the solid.
▶️ Answer/Explanation
Here, the diameter is \( D = (4 – y^{2}) – 0 = 4 – y^{2} \). Radius: \( r = \dfrac{4 – y^{2}}{2} \) Area of each cross section: \( A(y) = \dfrac{1}{2} \pi \left( \dfrac{4 – y^{2}}{2} \right)^{2} = \dfrac{\pi}{8} \left( 4 – y^{2} \right)^{2} \)
Volume: \( V = \displaystyle \int_{-2}^{2} \dfrac{\pi}{8} \left( 4 – y^{2} \right)^{2} \, dy \)
Since the function is even, \( V = \dfrac{\pi}{8} \cdot 2 \displaystyle \int_{0}^{2} \left( 4 – y^{2} \right)^{2} \, dy \)
Expand: \( \left( 4 – y^{2} \right)^{2} = 16 – 8y^{2} + y^{4} \)
Integrate: \( \displaystyle \int_{0}^{2} (16 – 8y^{2} + y^{4}) \, dy = \left[ 16y – \dfrac{8y^{3}}{3} + \dfrac{y^{5}}{5} \right]_{0}^{2} \)
Substitute: \( (32 – \dfrac{64}{3} + \dfrac{32}{5}) \)
Common denominator 15: \( \dfrac{480 – 320 + 96}{15} = \dfrac{256}{15} \)
Multiply by \( \dfrac{\pi}{8} \cdot 2 = \dfrac{\pi}{4} \): \( V = \dfrac{\pi}{4} \cdot \dfrac{256}{15} = \dfrac{64\pi}{15} \)
Final Answer: \( V = \dfrac{64\pi}{15} \)
