AP Calculus BC 9.5 Integrating Vector- Valued Functions Study Notes - New Syllabus
AP Calculus BC 9.5 Integrating Vector- Valued Functions Study Notes- New syllabus
AP Calculus BC 9.5 Integrating Vector- Valued Functions Study Notes – AP Calculus BC- per latest AP Calculus BC Syllabus.
LEARNING OBJECTIVE
- Solving an initial value problem allows us to determine an expression for the position of a particle moving in the plane.
Key Concepts:
- Integrating Vector-Valued Functions
Integrating Vector-Valued Functions
Integrating Vector-Valued Functions
Integration of vector-valued functions extends the idea of integrating scalar functions to functions whose outputs are vectors.
A vector-valued function is usually written as:
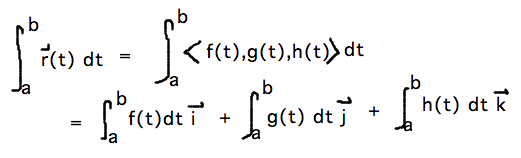
$ \mathbf{r}(t) = \langle f(t), \, g(t), \, h(t) \rangle $
Its definite or indefinite integral is computed by integrating each component function separately.
Definition:
If \(\mathbf{r}(t) = \langle f(t), g(t), h(t) \rangle\) is continuous on an interval, then:
$ \int \mathbf{r}(t) \, dt = \left\langle \int f(t) \, dt , \; \int g(t) \, dt , \; \int h(t) \, dt \right\rangle + \mathbf{C} $
where \(\mathbf{C} = \langle C_1, C_2, C_3 \rangle\) is a constant vector.
Key Notes:
- The process is component-wise integration.
- Units of the result depend on the context (position from velocity, velocity from acceleration, etc.).
- The constant of integration is itself a vector.
- Definite integrals are computed similarly, with limits applied to each component:
$ \int_{a}^{b} \mathbf{r}(t) \, dt = \left\langle \int_{a}^{b} f(t) \, dt , \; \int_{a}^{b} g(t) \, dt , \; \int_{a}^{b} h(t) \, dt \right\rangle $
Example
Find \(\displaystyle \int \langle t, t^{2}, e^{t} \rangle \, dt\).
▶️ Answer/Explanation
Integrate each component separately:
$ \int t \, dt = \frac{t^{2}}{2}, \quad \int t^{2} \, dt = \frac{t^{3}}{3}, \quad \int e^{t} \, dt = e^{t} $
Thus:
$ \int \langle t, t^{2}, e^{t} \rangle \, dt = \left\langle \frac{t^{2}}{2}, \frac{t^{3}}{3}, e^{t} \right\rangle + \langle C_{1}, C_{2}, C_{3} \rangle $
Example
Evaluate \(\displaystyle \int_{0}^{1} \langle 2t, \; \sin(\pi t), \; 3 \rangle \, dt\).
▶️ Answer/Explanation
Integrate each component over \([0,1]\):
$ \int_{0}^{1} 2t \, dt = \left[ t^{2} \right]_{0}^{1} = 1 $
$ \int_{0}^{1} \sin(\pi t) \, dt = \left[ -\frac{\cos(\pi t)}{\pi} \right]_{0}^{1} = \frac{-\cos(\pi) + \cos(0)}{\pi} = \frac{-(-1) + 1}{\pi} = \frac{2}{\pi} $
$ \int_{0}^{1} 3 \, dt = \left[ 3t \right]_{0}^{1} = 3 $
So the result is:
$ \int_{0}^{1} \langle 2t, \; \sin(\pi t), \; 3 \rangle \, dt = \langle 1, \frac{2}{\pi}, 3 \rangle $
Example
A particle has velocity \(\mathbf{v}(t) = \langle e^{t}, \; \cos t, \; t \rangle\) m/s at \(t\) seconds. If its position at \(t=0\) is \(\mathbf{r}(0) = \langle 1, 0, -1 \rangle\) m, find \(\mathbf{r}(t)\).
▶️ Answer/Explanation
Integrate the velocity to get position:
$ \int e^{t} \, dt = e^{t} + C_{1}, \quad \int \cos t \, dt = \sin t + C_{2}, \quad \int t \, dt = \frac{t^{2}}{2} + C_{3} $
Thus:
$ \mathbf{r}(t) = \langle e^{t} + C_{1}, \; \sin t + C_{2}, \; \frac{t^{2}}{2} + C_{3} \rangle $
Using \(\mathbf{r}(0) = \langle 1, 0, -1 \rangle\):
- From first component: \( e^{0} + C_{1} = 1 \implies 1 + C_{1} = 1 \implies C_{1} = 0 \)
- From second component: \( \sin 0 + C_{2} = 0 \implies 0 + C_{2} = 0 \implies C_{2} = 0 \)
- From third component: \( \frac{0^{2}}{2} + C_{3} = -1 \implies 0 + C_{3} = -1 \implies C_{3} = -1 \)
So:
$ \mathbf{r}(t) = \langle e^{t}, \; \sin t, \; \frac{t^{2}}{2} – 1 \rangle $
